Как доказать что сечение цилиндра прямоугольник

Урок «Понятие цилиндра»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Введем понятие цилиндра – геометрического тела.

Ну конечно, все вы видели много предметов в быту, похожих на данное тело.

Все прямые образуют поверхность, которая называется цилиндрической.

Каждая из этих прямых называется образующей цилиндрическую поверхность, а прямая, проходящая через центр окружности, – осью цилиндрической поверхности.

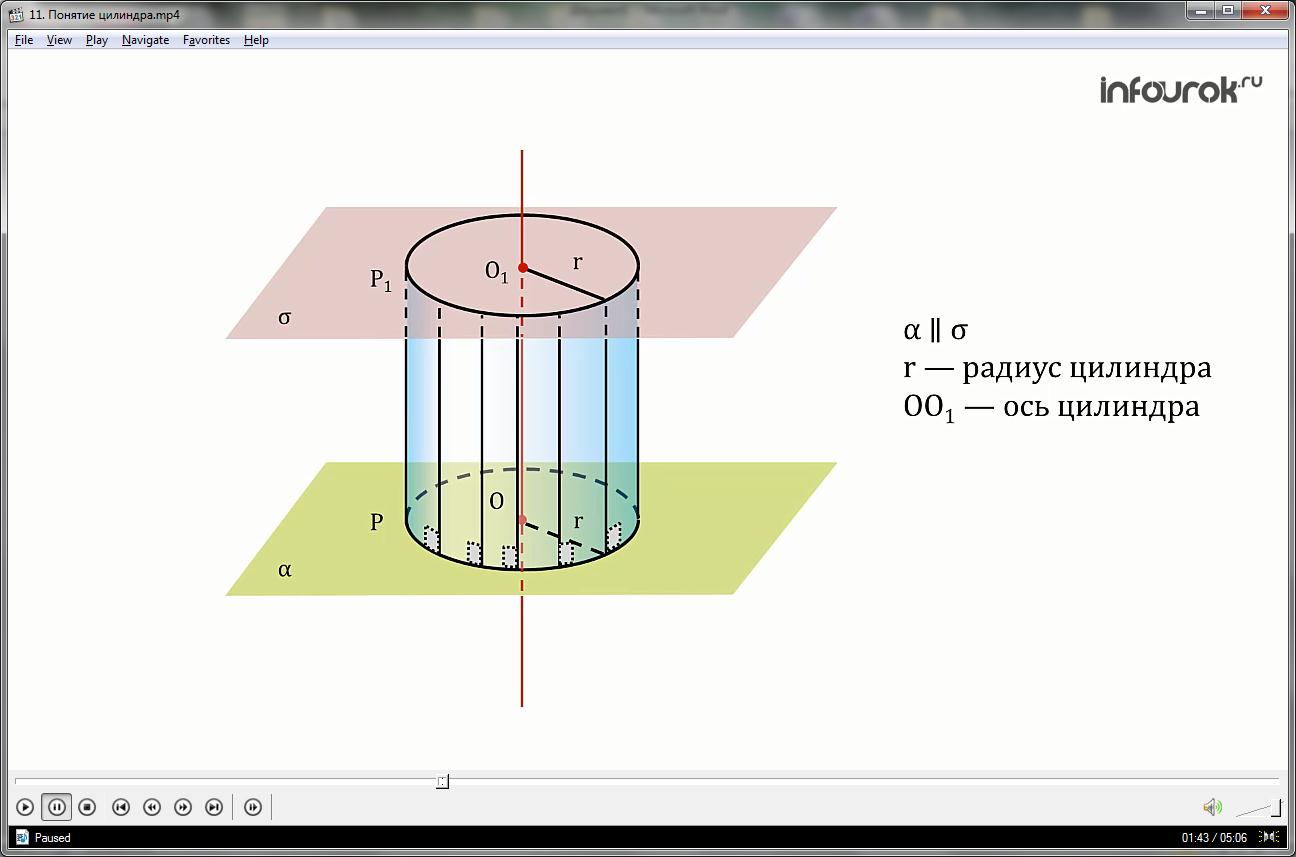
Далее проведем плоскость сигма, параллельную плоскости альфа, таким образом, что они отделят отрезки образующих, которые равны и параллельны между собой.

Ось цилиндрической поверхности пройдет через центр О1 окружности Р1, радиус окружностей будет равный r. Таким образом, мы получили цилиндр.

Цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя кругами, лежащими в параллельных плоскостях.

Ось ОО1 – называют осью цилиндра, отрезок образующей цилиндрической поверхности ТТ1– образующая цилиндра.

Цилиндрическая поверхность, т.е. поверхность, составленная из образующих, называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.

Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника вокруг стороны ОО1.

Рассмотрим сечение цилиндра.

1) Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.

2) Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Теперь давайте посмотрим, какие бывают цилиндры.

1) Прямые и наклонные, в зависимости от того, перпендикулярны или наклонны плоскости оснований к образующим.

2) Сложные цилиндры.

изображён цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком.

На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскости оснований (наклонный цилиндр).

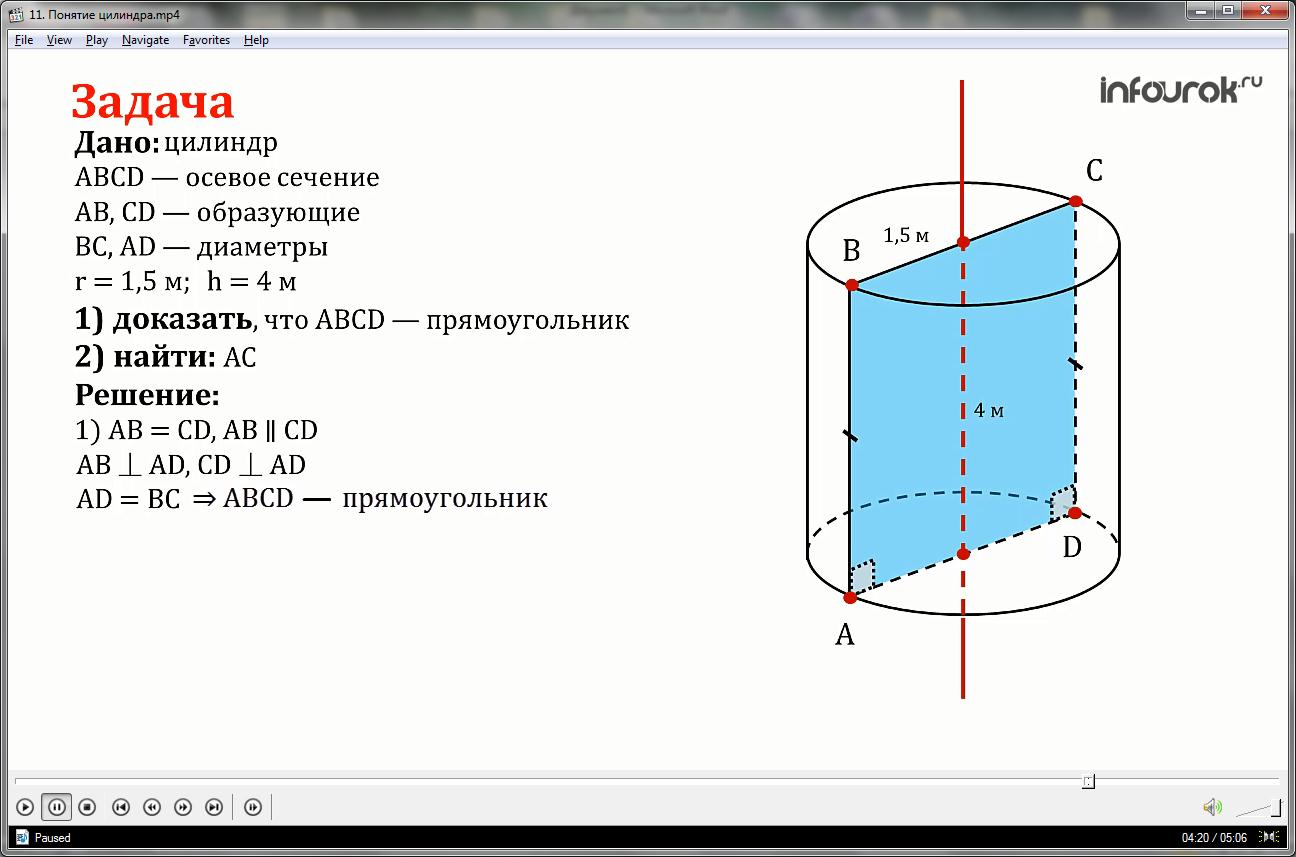
Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого – образующие, а две другие – диаметры оснований цилиндра. Найти диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота равна 4 м.

1) так как АВ и CD – образующие то они равны и параллельны, и по определению образующих цилиндра АВ и CD перпендикулярны основанию.

AD и BC равны как диаметры оснований,

следовательно, четырехугольник ABCD по признаку параллелограмма и определению является прямоугольником.

2) Диагональ АС делит прямоугольник на два равных прямоугольных треугольника, тогда,

из прямоугольного треугольника АВС находим АС: по теореме Пифагора АС равна корню квадратному из суммы квадратов сторон АВ и АС, где АВ равна высоте цилиндра, а ВС диаметру основания то есть двум радиусам.

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класса

Урок №6. Тела вращения. Цилиндр

Перечень вопросов, рассматриваемых в теме:

Цилиндрическая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность.

Эти прямые – образующие цилиндрической поверхности.

Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось цилиндрической поверхности.

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами.

Круги – основания цилиндра; отрезки образующих, заключённые между основаниями – образующие цилиндра; образованная ими часть цилиндрической поверхности – боковая поверхность.

Ось цилиндрической поверхности называется осью цилиндра.

Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Сечение – изображение фигуры, образованной рассечением тела плоскостью.

Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.

Развёртка боковой поверхности цилиндра – прямоугольник, одна сторона которого равна высоте цилиндра, а другая длине окружности основания.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций: базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-79.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные определения

Цилиндрической поверхностью называется поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность (см.рис.).

Сами прямые называют образующими цилиндрической поверхности.

Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости 𝛂, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость 𝛃, которая будет параллельна плоскости 𝛂, то отрезки образующих, заключённые между плоскостями 𝛂 и 𝛃 будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости 𝛃, дают окружность, равную окружности, лежащей в плоскости 𝛂.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях 𝛂 и 𝛃) называется цилиндром.

Ось цилиндрической поверхности называется осью цилиндра.

Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

2. Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

3. Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: S_бок=2𝛑RL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: S_полн=2𝛑R(R+L).

Примеры и разбор решения заданий тренировочного модуля

Выберите значение площади его боковой поверхности

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

Найдем сторону АВ сечения.

НВ=ОН·tg60 0 =1·.

S_сеч=6·=18

3. Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

По условию задачи L=R+6.

Получили квадратное уравнение относительно радиуса:

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Источник

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Основные элементы цилиндра

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Источник

Презентация к уроку геометрии «Цилиндр. Решение задач» (11 класс)

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Филиал ОГБОУ СПО «Рязанский педагогический колледж» в г.Касимове Презентация к уроку геометрии Цилиндр. Решение задач Подготовила преподаватель И.И.Колоколенкова

Цели урока: формировать навыки решения задач на нахождение элементов цилиндра, площади поверхности цилиндра; закрепить знания, умения учащихся по изучаемой теме; развивать самостоятельность учащихся в работе над задачами.

План урока 1. Организационный момент 2. Актуализация знаний: а)Устная работа с классом. I. Вопросы. II.Решение задач по готовому чертежу б) Проверка домашнего задания (три ученика работали у доски во время устной работы класса). 3. Фронтальная работа по слайдам 4. Работа в группах. Решение задач по готовым чертежам. 5. Физкультминутка. 6.Разноуровневая самостоятельная работа 7. Подведение итогов урока

Устная работа с классом а)Вопросы 1. Укажите среди окружающих вас предметов объекты, имеющие цилиндрическую форму. 2. Дайте определение цилиндра и его основных элементов. 3. Что такое осевое сечение цилиндра? Каков его вид? 4. Может ли осевое сечение быть: а) прямоугольником; б) квадратом; в) трапецией? Почему? 5. Цилиндр катится по плоскости. Какая фигура получается при движении его оси?

Фронтальная работа по слайдам

Концы отрезка АВ, равного а, лежат на окружностях оснований цилиндра. Радиус цилиндра равен r, высота равна h, а расстояние между прямой АВ и осью 001 цилиндра равно d. 1. Объясните, как построить отрезок, длина которого равна расстоянию между скрещивающимися прямыми АВ и 001. 2. Составьте (и объясните) план нахождения величины d по заданным величинам а, h, r. 3. Составьте (и объясните) план нахождения h по заданным величинам а, r, d.

Работа в группах. Решение задач по готовым чертежам

Задача №1. 1. OD = R, AD = 3. 2. ∆ADС – прямоугольный,так как AD = 4, то АС = 5 (пифагорова тройка). (Ответ: 5.)

Задача №5 Дано: Sбок./Sосн. =1/2 Найти: H/2R Решение: 1. Sбок./Sосн = 2πRH/πR2 = 2H/R = ½. 2. 2H/R = ½. ═ H/2R = 1/8.

Физкультминутка Мы с вами хорошо поработали, повторили всё необходимое. Прежде чем выполнить самостоятельную работу проведём физкультминутку. Сядьте удобнее, расслабьтесь. Каждое задание выполняем по 10 раз. Обведите верхнее основание цилиндра глазами по часовой стрелке, а нижнее – против часовой стрелки. Проведите глазами по оси цилиндра сверху вниз. Проведите глазами по диаметру справа налево. Закройте глаза. Откройте глаза. С новыми силами приступаем к работе.

Разноуровневая самостоятельная работа

1уровень Вариант I 1. Радиус цилиндра равен 10 см. Сечение, параллельное оси цилиндра и уда­ленное от нее на 8 см, имеет форму квадрата. Найти площадь сечения. 2. Диагональ осевого сечения цилиндра равна 8 √2 дм и образует с плоскостью ос­нования цилиндра угол 45°. Найдите площадь полной поверхности цилиндра. Вариант II 1. Высота цилиндра равна 16 см. На расстоянии 6 см от оси цилиндра проведе­но сечение, параллельное оси цилиндра и имеющее форму квадрата. Найди­те радиус цилиндра. 2. Диагональ осевого сечения цилиндра равна 8 дм и составляет с образующей угол 60°. Найдите площадь полной поверхности цилиндра. II уровень Вариант I 1. Прямоугольник вращается вокруг одной из своих сторон, равной 5 см. Пло­щадь боковой поверхности цилиндра, полученного при вращении, равна 100π см2. Найдите площадь прямоугольника. 2. Хорда нижнего основания цилиндра отсекает от окружности основания дугу в 120°. Отрезок, соединяющий центр верхнего основания с серединой данной хорды, равен 4√2 см и образует с плоскостью основания угол 45°. Найдите площадь осевого сечения цилиндра. Вариант II 1. Прямоугольник, одна из сторон которого равна 5 см, вращается вокруг неиз­вестной стороны. Найдите площадь прямоугольника, если площадь боковой поверхности цилиндра, полученного при вращении, равна 60π см2. 2. Хорда нижнего основания цилиндра удалена от центра нижнего основания на 2√3 см и отсекает от окружности основания дугу в 60°. Отрезок, соеди­няющий центр верхнего основания с одним из концов данной хорды, образу­ет с осью цилиндра угол 45°. Найдите площадь осевого сечения цилиндра.

Подведение итогов урока на уроке было интересно и все понятно на уроке было интересно, но возникли затруднения на уроке было все понятно, но неинтересно на уроке ничего не заинтересовало на уроке было все непонятно и неинтересно

Источник

Тема урока: «Решение задач по теме «Цилиндр»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Тема урока: Решение задач по теме «Цилиндр».

Предмет: геометрия 11 класс

Учебник: «Геометрия 10-11», Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцева и др., 2009г

Место занятия в структуре образовательного процесса: урок по учебному плану.

Форма урока: комбинированный

1. Закрепить у учащихся знания о теле вращения – цилиндре (определение, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра).

2. Сформировать навыки решения типовых задач.

2. Развивать пространственные представления на примере круглых тел.

3. Продолжить формирование логических и графических умений

1. Научить учащихся строить сечение цилиндра плоскостью параллельной оси цилиндра и перпендикулярной оси цилиндра.

2. Научить учащихся применять формулы полной и боковой поверхностей цилиндра при решении задач.

Учащиеся должны уметь изображать цилиндр и его сечения на бумаге.

Учащиеся должны уметь применять формулы для вычисления площадей полной и боковой поверхностей при решении задач.

Учащиеся должны уметь решать простейшие геометрические задачи, связанные с цилиндром и сечениями цилиндра.

Организационный момент (  2 минуты)

Повторение ранее изученного материала (  10 минут)

Закрепление (  20 минут)

Обучающая самостоятельная работа (10 минут)

Итог урока (3 минуты)

1. Организационный момент.

2. Повторение ранее изученного материала.

Учащимся предлагается заполнить лист с заданиями.

Возможен вариант работы с применением копировки (в таком случае один экземпляр сдается учителю, а второй ребенок проверяет в ходе дальнейшей работы на уроке).

1. Нанесите на рисунок основные элементы цилиндра.

2
.Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра; в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Какая фигура получается в каждом случае?

3. Запишите формулы для вычисления площади поверхности цилиндра.

Что можно найти по этим формулам? Что должно быть известно в этих случаях?

Учащиеся сдают листы с заданием.

Фронтальный опрос (с целью обобщения знаний и проверки выполненной работы)

Какая фигура называется цилиндром?

Почему цилиндр называют телом вращения?

Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.

Назовите виды цилиндров?

Наклонные цилиндры, прямые цилиндры, цилиндрические поверхности

Назовите элементы цилиндра.

Основания цилиндра – равные круги, расположенные в параллельных плоскостях

Радиус цилиндра – это радиус его основания.

Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).

Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.

Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра .

Что представляет собой развертка цилиндра?

Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C , где H – высота цилиндра, а C – длина окружности основания.

Как найти площадь боковой поверхности цилиндра?

Как найти площадь полной поверхности цилиндра?

Назовите основные виды сечений цилиндра. Какая фигура получается в каждом случае?

Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники

Сечение плоскостью, параллельной оси цилиндра. В сечении – прямоугольники.

Сечение плоскостью перпендикулярной оси цилиндра . В сечении круги, равные основанию.

Приведите примеры использования цилиндров.

Цилиндрическая гастрономия. Цилиндрическая архитектура. Цилиндры фараона (выступление ученика 1-2 мин).

3. Закрепление материала. Решение задач.

Ученики видят список задач для классной работы. По желанию учащиеся имеют возможность решать с опережением на оценку.

№1. (задача с практическим содержанием).

Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке.

№ 2 (523). Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So цилиндра.

4. Обучающая самостоятельная работа

Самостоятельная работа по вариантам. (Возможна организация парной работы).

1) Докажите, что сечение цилиндра плоскостью g есть прямоугольник.

5. Подведение итогов урока.

1) Домашнее задание.

Повторить стр.130-132, гл. 1, п.59-60, №530, № 537.

2) Выставление оценок за работу на уроке.

Что нового вы узнали на уроке?

Какое у вас настроение в конце урока?

Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня?

Слайд 1: Тема занятия

Слайды 2-3. Общее определение цилиндрической поверхности, актуализация знаний (без анимации)

Слайды 4-5. Наклонный и прямой цилиндр (без анимации).

Слайд 6. Развертка цилиндра. По щелчку ЛКМ появляются формулы площади основания, боковой поверхности, площади полной поверхности.

Слайд 7. Сечение цилиндра плоскостью.

Слайды 8-10. Примеры использования цилиндров в жизни.

Слайд 11. Задача с практическим содержанием.

Слайд 12. Задача №523.

Слайд 13. Задача №525.

Слайд 14. Задача №527. Щелчком по знаку вопроса (триггер) мы переходим на слайд с подробным описанием построения расстояния между скрещивающимися прямыми. Если нет в этом необходимости, можно продолжить решение задачи дальше и увидеть данное построение без подробного описания.

Слайд 15. Скрытый слайд нахождение расстояния между скрещивающимися прямыми, возврат по стрелке назад.

Слайд 16. Задача №532.

Слайд 17. Задание для самостоятельной работы (два варианта).

Триггер щелчком по кнопке «ответ» появляется результат задачи.

Слайд 18. Домашнее задание, рефлексия.

Слайд 19. Использованные источники (скрытый слайд).

1. Изучение геометрии в 10-11 классах: кн. Для учителя/С.М. Саакян, В.Ф. Бутузов. – 4-е издание, М.: Просвещение, 2010.

2. Рабочая тетрадь к учебнику «Геометрия 10-11 класс» Л.С. Атанасян, М.: Просвещение, 2010

3. С D «Виртуальная школа Кирилла и Мефодия: Геометрия-11 класс»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-404598

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Школьники из Москвы выступят на Международной олимпиаде мегаполисов

Время чтения: 3 минуты

Время чтения: 2 минуты

Утверждены сроки заключительного этапа ВОШ

Время чтения: 1 минута

Во Франции планируют ввести уголовное наказание за буллинг в школе

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник