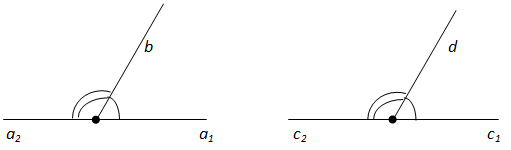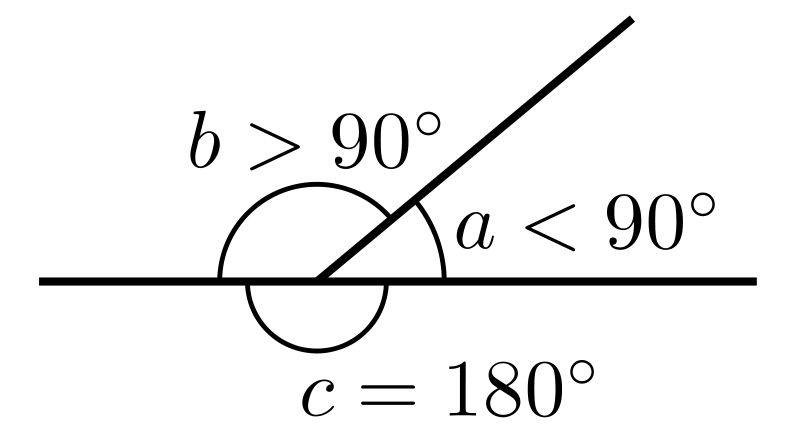Как доказать что смежные углы равны 180

Как доказать что смежные углы равны 180

Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
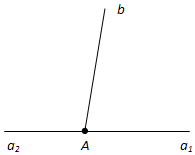
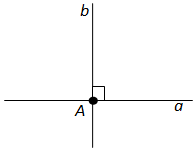
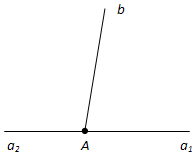
На рисунке 31 углы (a₁b) и (a₂b) смежные. У них сторона b общая, а стороны a₁ и a₂ являются дополнительными полупрямыми.

Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.

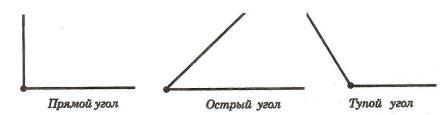
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.

Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
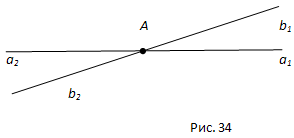
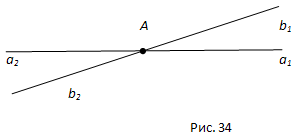
Доказательство. Пусть (a₁b₁) и (a₂b₂)- данные вертикальные углы (рис. 34). Угол (a₁b₂) является смежным с углом (a₁b₁) и с углом (a₂b₂). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a₁b₁) и (a₂b₂) дополняет угол (a₁b₂) до 180°, т.е. углы (a₁b₁) и (a₂b₂) равны. Что и требовалось доказать.

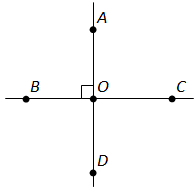
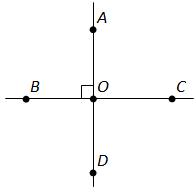
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.

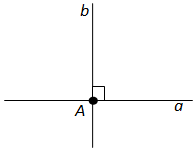
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».

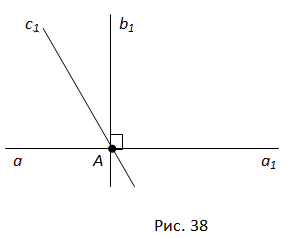
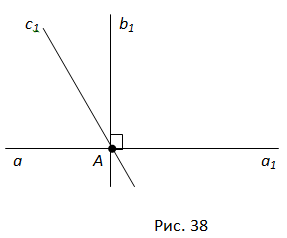
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c₁ полупрямую этой прямой, лежащую в одной полуплоскости с лучом b₁.
Углы (a₁b₁) и (a₁c₁), равные каждый 90°, отложены в одну полуплоскость от полупрямой a₁. Но от полупрямой a₁ в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.

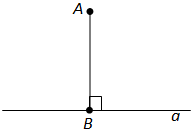
Вопрос 11. Что такое перпендикуляр к прямой?
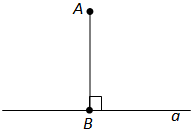
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.

Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

Источник

Смежные углы

Что такое смежные углы? Какие у них свойства?

Определение.

Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.

∠1 и ∠2 — смежные углы

Сколько смежных углов образуется при пересечении двух прямых?

При пересечении двух прямых образуется четыре пары смежных углов:

Но, так как ∠1 =∠4, ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.

Свойство смежных углов.

Сумма смежных углов равна 180º.

1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.

∠AOC и ∠BOC — смежные,

∠AOC на 42º больше, чем ∠BOC

Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.

Значит, ∠BOC= 69º, ∠AOC=69+42=111º.

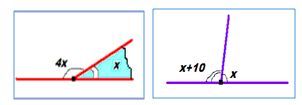
2) Найти смежные углы, если их градусные меры относятся как 4:5.

Значит, смежные углы равны 4∙20=80º и 5∙20=100º.

3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.

Дано: AB и CD — прямые, O — точка их пересечения,

∠AOD в 5 раз больше, чем ∠BOD

При пересечении двух прямых образуются смежные и вертикальные углы. Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD — смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.

Значит, ∠BOD=30º, ∠AOD=5∙30=150º.

Могут ли смежные углы быть равными?

Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.

угол, смежный с прямым, есть прямой угол.

Могут ли два смежных угла быть тупыми? Острыми?

Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.

Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.

Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).

Источник

Как доказать что смежные углы равны 180

Угол – это геометрическая фигура ( рис.1 ), образованная двумя лучами OA и OB ( стороны угла ), исходящими из одной точки O ( вершина угла ).

СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.

Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.

На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.

Теорема о смежных углах

Теорема: сумма смежных углов равна 180°

Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.

Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.

Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.

Определение 4. Угол, меньший 90 градусов, называется острым углом.

Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.

Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.

Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
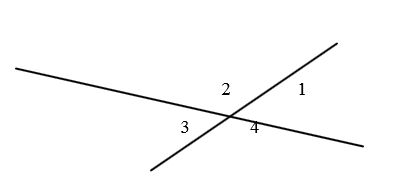
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.

Интересный факт

Связь математики с музыкой

Так же предложу вашему внимаю забавную пародию про спор двух математиков =)

Геометрия вокруг нас

Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились. Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.

1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?

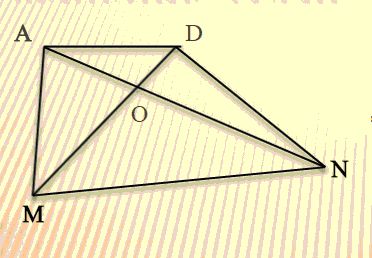
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.

Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.

Решение задач

Математический диктант на повторение ранее выученного материала

1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
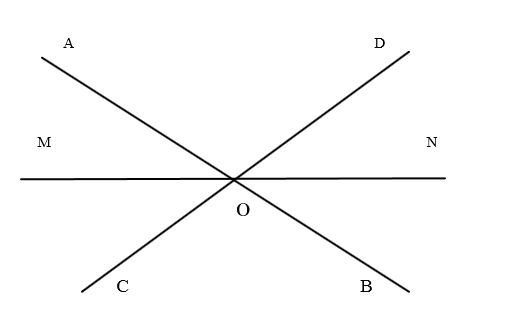
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.

3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:

а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.

Итог урока

1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.

1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1 : 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.

Источник

Как доказать что смежные углы равны 180

Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a₁b) и (a₂b) смежные. У них сторона b общая, а стороны a₁ и a₂ являются дополнительными полупрямыми.

Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.

Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.

Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a₁b₁) и (a₂b₂)- данные вертикальные углы (рис. 34). Угол (a₁b₂) является смежным с углом (a₁b₁) и с углом (a₂b₂). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a₁b₁) и (a₂b₂) дополняет угол (a₁b₂) до 180°, т.е. углы (a₁b₁) и (a₂b₂) равны. Что и требовалось доказать.

Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.

Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».

Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c₁ полупрямую этой прямой, лежащую в одной полуплоскости с лучом b₁.
Углы (a₁b₁) и (a₁c₁), равные каждый 90°, отложены в одну полуплоскость от полупрямой a₁. Но от полупрямой a₁ в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.

Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.

Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

Источник

Геометрия. 7 класс

Конспект урока

Смежные и вертикальные углы. Аксиомы и теоремы

Перечень вопросов, рассматриваемых в теме:

Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.

Свойства смежных углов:

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Свойство вертикальных углов: вертикальные углы равны.

Аксиома– положение, принимаемое без доказательств.

Теоретический материал для самостоятельного изучения

Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.

Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.

Давайте докажем это свойство.

Укажем ещё одно свойство смежных углов.

Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.

Углы, которые не являются смежными:

∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.

Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов

Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.

На предыдущих уроках вы познакомились с понятием аксиомы.

В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Используя чертёж, найдите угол ∠ВОК.

№2. Тип задания: единичный / множественный выбор.

Используя чертёж, найдите угол ∠AOD.

№3. Тип задания: выделение цветом.

Выделите верный ответ из списка:

60 0 ; 30 0 ; 75 0 ; 90 0

Источник