Как доказать что треугольник египетский

Египетский треугольник

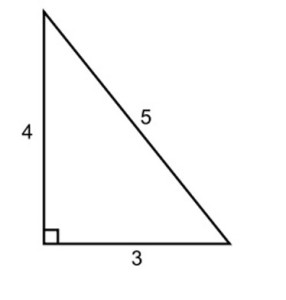
Египетский треугольник – прямоугольный треугольник с отношением сторон 3:4:5. Это наиболее простой из треугольников, стороны и площади которых выражаются целыми числами. Он представляет собой прекрасную иллюстрацию теоремы Пифагора – действительно, квадрат его гипотенузы (25) очевидно равен сумме квадратов его катетов (9 и 16). Предполагается даже, что именно знакомство с египетским треугольником сподвигло Пифагора на формулировку его теоремы. Впрочем, как всегда в подобных случаях, историки древности, которые не являются специалистами ни в одной другой области знания, кроме истории (и уж точно плохо смыслят в математике), могут ошибаться.

Так или иначе, имеются многочисленные указания на то, что теорема Пифагора вообще и египетский треугольник в частности были известны и широко использовались за много веков до Пифагора и далеко за пределами Египта – в Месопотамии, в долине Инда, в древнем Китае. И вправду, корень многих знаний следует искать, наверное, в практической деятельности человека. Как только возникла необходимость возводить здания и сооружения, человек эмпирическим путём пришёл к пониманию важности прямых углов. А как отмерить прямой угол, не имея геодезических приборов?

Оказывается, очень просто. Берём верёвку и делим её на 12 равных частей – например, при помощи складывания. Выбираем отрезок верёвки, равный 5, так, чтобы он находился межды двумя другими, равными 3 и 4. Выпрямляем его и фиксируем на ровном участке земли при помощи двух колышков. А затем натягиваем концы верёвки и сводим их в одну точку, чтобы получился треугольник. Прямоугольный, египетский.

«Делай, как делается». Знаменитая древнеегипетская пословица, дошедшая до наших дней. У нас её обычно понимают, как мудрое наблюдение: если так получается, значит, так правильно. Но при этом часто забывают культурно-исторический контекст Древнего Египта. Всеми работами руководили жрецы – члены замкнутой касты харнителей священного, древнего знания. Поэтому «делай, как делается» в древнеегипетском контексте наверняка значило «делай как говорят и не задавай лишних вопросов». То есть жрецы знали не только, «как» делать, чтобы «делалось», но и «почему», и это зание было скрыто от непосвящённых.

Мы тоже хотим знать, «почему». Нам недостаточно «как». Человеческий ум будоражат разнообразные загадки, и так, наверное, будет всегда. Египетский треугольник, хоть и известен с незапамятных времён – одна из таких загадок.

Начнём с того, что он красив. Его форма проста и гармонична, на него приятно смотреть. И с ним легко работать, используя самые простые инструменты – линейку и циркуль. Он, казалось бы, даже приглашает поработать с ним. Что ж, примем приглашение и посмотрим, что у нас получится.

Несколько простых построений, в числе которых – квадраты гипотенузы и катетов, а также симметричные отображения, сразу дают нам красивые, грмоничные фигуры. Здесь мы видим и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих (возрастающих) по размерам египетских треугольников в соответствии с правилом золотого сечения. Удивительное богатство гармоничных пропорций. И кажется, что ещё немного, и неразрешимая задача о квадратуре круга будет решена.

Впрочем, не станем уподобляться безумцам, которые изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Ограничимся констатацией бесконечных возможностей создания красоты и гармонии при помощи простой верёвки, разделённой на 12 равных частей. В том числе и картины в стиле арифмизма. Картины, которая, в соответствии с определением, изображает законченное арифметическое выражение: 9 + 16 = 25. Математический и геометрический смысл очевиден. Тайное значение – наверное, на то оно и тайное, чтобы таковым оставаться. А многозначительная и почти мистическая эстетика данных форм пусть радует глаз и будоражит воображение.

Источник

Египетский треугольник и обратная теорема Пифагора

Математический лайфхак из обасти геометрии “Как при помощи простой верёвки получить треугольник с прямым углом”.
Египтяне 4000 лет назад для строительства пирамид использовали метод получения прямоугольного треугольника при помощи верёвки разделенной на 12 равных частей.

Понятие “египетский треугольник”.

Почему треугольник со сторонами 3, 4, 5 называют египетским?

А всё дело в том, что строителям Древнего Египта пирамид нужен был простой и надежный метод построения треугольника с прямым углом. И вот как они это реализовывали. Верёвку разбивали на двеадцать равновеликих частей, обозначив границы между соседними частями; концы верёвки соединяли. После этого 3 человека натягивали верёвку таким образом, чтобы она образовала треугольник, причем расстояния между каждыми двумя египтянами, тянущими веревку, составляли соответственно три части, четыре части и пять частей. Получался треугольник с прямым углом с катетами в три и четыре части и гипотенузой в пять частей. Известно, прямым был угол между сторонами в три и четыре части. Как известно, древнеегипетских землемеров, которые кроме обмеривания земельных наделов занимались построениями на местности, в древнем Египте их называли гарпедонаптами (что буквально переводится как «натягивающие верёвки»). Гарпедонапты занимали 3 место в иерархии жрецоы Древнего Египта.

Обратная теорема Пифагора.

Но из-за чего треугольник со сторонами 3, 4, 5 окажется прямоугольным? Большинство ответили бы на данный вопрос, что данный факт это теорема Пифагора: так как три в квадрате плюс четыре в квадрате равняется пяти в квадрате. Но теорема Пифагора говорит, что если треугольник с прямым углом, то тогда сумма квадратов 2-х его сторон равняется квадрату третьей. Здесь мы имеем дело с теоремой, обратной теореме Пифагора: если сумма квадратов 2-х сторон треугольника равна квадрату третьей, то тогда треугольник — прямоугольный.

Обрисованное практическое приложение обратной теоремы Пифагора относиться к далёкому прошлому. Едва ли кто-либо получает прямые углы таким методом сегодня. Но тем не менее данный способ является отличным математическим лайфхаком и может быть применён Вами в любой жизненной ситуации.

Метод определения прямоугольного треугольника при помощи верёвки из мира практики переместился в мир идей, подобно тому как многое из материальной культуры древности вошло в духовную культуру нынешней действительности.

Источник

Самое интересное, что такое название фигуре дали не Египтяне, а эллины, прибывшие в 5-7 веках до нашей эры в Египет. Чем же так замечателен египетский треугольник?

Три главных его свойства:

1. Всего его стороны целочисленны и рациональны: к тому же 3,4,5 минимальные из вещественных чисел.

2. Египетский треугольник — родоначальник так называемых героновских треугольников (знакомая фамилия? Помните формулу из школьного курса геометрии?), а точнее самый простой из них.

3. Радиус вписанной в треугольник окружности равен единице.

А теперь, дорогой читатель, давай умножим все стороны простейшего египетского треугольника на любое вещественное число, для простоты на 3. Тогда получим а=3*3=9, b=4*3=12 и c=5*3=15. Треугольник с такими сторонами — тоже прямоугольный

И что? Возразит читатель! Это же простая математика про извлечение корней! Что здесь такого? И будет прав. Если он живет в 21 веке. Но будет очень неправ, если он родился в Древнем Египте. Так как среди наших читателей таковых вроде как нет, попытаюсь объяснить.

Представьте, что вы древнеегипетский землемер и вам нужно разметить квадратный фундамент, например, для пирамиды, имеющий вид квадрата со стороной 100 метров. Как решить эту проблему? Да легко! Берем веревку длиной 100 метров, привязываем его к колышку и идем в одну сторону, делаем отметку. Возвращаемся и идем под углом 90 градусов в другую сторону на 100 метров. И получаем нечто такое:

Явно не похожее на квадрат в основании, скорее на ромб. Так где же зарыта собака? Ответ: в определении угла в 90 градусов. Попробуйте на досуге даже обычной линейкой разметить квадрат два на два метр и получите расхождение. что уж говорить, когда стороны в 50 раз больше?

Что же делать землемеру? На помощь приходит математика.

Берем веревку длиной 25 метров. На другой длинной веревке откладываем 12 этих веревок и получаем 300-метровый отрезок с нанесенными отметками каждые 25 метров. Теперь все абсолютно просто: надо из это веревки построить треугольник, с длинами в 3,4 и 5 отрезков соответственно. Магия такова, что в таком случае у Вас всегда получится прямой угол! А все остальное — дело техники. В завершении видео:

Спасибо за любовь к математике! Жду Вас снова!

Источник

Малоизвестное обобщение теоремы Пифагора

Вокруг да около

История теоремы Пифагора уходит в века и тысячелетия. В этой статье, мы не будем подробно останавливаться на исторических темах. Для интриги, скажем только, что, по-видимому, эту теорему знали еще древне-египетские жрецы, жившие более 2000 лет до нашей эры. Для тех, кому любопытно, вот ссылка на статью в Википедии.

Прежде всего, хочется для полноты изложения привести здесь доказательство теоремы Пифагора, которое, по моему мнению, наиболее элегантно и очевидно. На рисунке выше изображено два одинаковых квадрата: левый и правый. Из рисунка видно, что слева и справа площади закрашенных фигур равны, так как в каждом из больших квадратов закрашено по 4 одинаковых прямоугольных треугольника. А это означает, что и незакрашенные (белые) площади слева и справа тоже равны. Замечаем, что в первом случае площадь незакрашенной фигуры равна , а во втором — площадь незакрашенной области равна . Таким образом, . Теорема доказана!

Зарождение идеи

В этой статье я хочу не только рассказать что-то новое и познавательное о теореме Пифагора, но и поделиться своей историей о том, как в моей голове зародилась интересная идея, которую я сумел сформулировать, доказать и даже предположил возможность обобщения на более высокую размерность. Но обо всем по порядку.

Египетские треугольники

Во-первых, это красивые математические объекты. А во-вторых, с ними очень удобно решать задачи! Нет никаких квадратных корней и иррациональных чисел в ответе.

Загадочные четверки

Заметив такое удивительное совпадение, я стал думать. Вопрос, который меня занимал в связи с этим загадочным обстоятельством, наличием не только троек, но и четверок, обнаруживающих свойства египетского треугольника, был таков: «А что бы это все могло значить?» Я перебирал варианты, какие только приходили в голову. В фантазии себя никак не ограничивал. Много раз садился за стол, выписывал известные мне наборы четверок и вдумчиво на них смотрел… часами… без перерыва… и… ничего не происходило. У меня был школьный товарищ Саня, с которым я как-то поделился своими идеями. Но его больше интересовали гуманитарные науки. Он стал юристом и сейчас служит в звании майора милиции. Саня сказал мне примерно следующее:«Вот странный ты человек. Делать тебе больше нечего. Мало тебе задают домашек? Хватит думать о всякой ерунде!». А, надо сказать, думал я, не переставая, и думал много лет, время от времени возвращаясь к этой загадке. Еще будучи школьником, я сделал вывод, что это, вероятнее всего, имеет отношение к великой теореме Ферма (на которую я тоже много раз подолгу смотрел). Шли годы. Ничего не получалось. Озарение не приходило. И я понял, что, вероятно, дальше чем «что-то связанное с теоремой Ферма» я никуда уже не продвинусь. Но не тут то было

Шерлок нашел зацепку

Итак, в 2014 году ехал я в автобусе по Новосибирску. А может быть это было метро. Дорога не близкая. Заняться нечем. И в очередной раз решил я подумать о моей школьной загадке. И вот что я подумал.

Как же назвать эти числа? Треугольниками не назовешь, ведь четыре числа никак не могут образовать треугольник. И тут! Как гром среди ясного неба

Раз есть такие четверки чисел, значит должен быть геометрический объект с такими же свойствами, отраженными в этих числах!

Теперь осталось только подобрать какой-то геометрический объект под это свойство, и все встанет на свои места! Конечно, предположение было чисто гипотетическое, и никакого подтверждения под собой не имело. Но что если это так!

Начался перебор объектов. Звезды, многоугольники, правильные, неправильные, с прямым углом и так далее и тому подобное. Опять ничего не подходит. Что делать? И в этот момент Шерлок получает свою вторую зацепку.

Надо повысить размерность! Раз тройке соответствуют треугольник на плоскости, значит четверке соответствует нечто трехмерное!

О нет! Опять перебор вариантов! А в трехмерии гораздо, гораздо больше всевозможных геометрических тел. Попробуй перебрать их все! Но не все так плохо. Есть же еще прямой угол и другие зацепки! Что мы имеем? Египетские четверки чисел (пусть будут египетские, надо же их как-то называть), прямой угол (или углы) и некий трехмерный объект. Дедукция сработала! И… Полагаю, что догадливые читатели уже поняли, что речь идет о пирамидах, у которых при одной из вершин все три угла — прямые. Можно даже назвать их прямоугольными пирамидами по аналогии с прямоугольным треугольником.

Новая теорема

Итак, у нас есть все что нужно. Прямоугольные (!) пирамиды, боковые грани-катеты и секущая грань-гипотенуза. Пришло время нарисовать еще одну картинку.

Теорема Пифагора для прямоугольной пирамиды

На картинке изображена пирамида с вершиной в начале прямоугольных координат (пирамида как бы лежит на боку). Пирамида образована тремя взаимно-перпендикулярными векторами, отложенными из начала координат вдоль координатных осей. То есть каждая боковая грань пирамиды — это прямоугольный треугольник с прямым углом при начале координат. Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.

Теорема

Пусть есть прямоугольная пирамида, образованная тремя взаимно-перпендикулярными векторами , у которой площади граней-катетов равны — , и площадь грани-гипотенузы — . Тогда

Альтернативная формулировка: У четырехгранной пирамиды, у которой при одной из вершин все плоские углы прямые, сумма квадратов площадей боковых граней равна квадрату площади основания.

Разумеется, если обычная теорема Пифагора формулируется для длин сторон треугольников, то наша теорема формулируется для площадей сторон пирамиды. Доказать эту теорему в трех измерениях очень просто, если вы немного знаете векторную алгебру.

Доказательство

где .

Площадь представим как половину площади параллелограмма, построенного на векторах и

Как известно, векторное произведение двух векторов — это вектор, длина которого численно равна площади параллелограмма, построенного на этих векторах.
Поэтому

Что и требовалось доказать!

ЭВРИКА!

Моему восторгу не было границ! Я буквально прыгал от счастья. Конечно, это не бог весть какая сложная теорема, и доказательство очень простое, но ведь сам. И до меня — никто! Я был в этом искренне убежден в течение около года. Попытки найти хоть какие-то свидетельства о том, что это уже известно и доказано терпели неудачу одна за другой, и я думал, что совершил открытие. Это непредаваемое чувство! Я хотел поделиться этой теоремой со всем миром. Говорил о ней друзьям, знакомым математикам, просто знакомым с техническим/математическим образованием и без. Никто не разделял моего восторга и энтузиазма. Всем было попросту безразлично. Будто бы я не придумал и доказал теорему, а просто в магазин за хлебом сходил. Ну и что тут такого? Вот уж действительно… Как говорится, «Как скучно мы живём! В нас пропал дух авантюризма, мы перестали лазить в окна к любимым женщинам, мы перестали делать большие хорошие глупости.» (из фильма «Ирония судьбы»).

Конечно, как у человека, профессионально занимающегося исследованиями, подобное в моей жизни уже случалось, и не раз. Но этот момент был самым ярким и самым запоминающимся. Я испытал полную гамму чувств, эмоций, переживаний первооткрывателя. От зарождения мысли, кристализации идеи, нахождения доказательства — до полного непонимания и даже неприятия, которое встретили мои идеи у моих друзей, знакомых и, как мне тогда казалось, у целого мира. Это было уникально! Я словно почувствовал себя в шкуре Галлилея, Коперника, Ньютона, Шредингера, Бора, Эйнштейна и многих многих других открывателей.

Послесловие

В жизни, все оказалось гораздо проще и прозаичнее. Я опоздал… Но на сколько! Всего-то навсего 18 лет! Под страшными продолжительными пытками и не с первого раза Гугл признался мне, что эта теорема была опубликована в 1996 году!

Вот ссылка на статью:

Статья опубликована издательством Техасского технического университета. Авторы, профессиональные математики, ввели терминологию (которая, кстати, во многом совпала с моей) и доказали также и обобщенную теорему справедливую для пространства любой размерности большей единицы. Что же произойдет в размерностях более высоких, чем 3? Все очень просто: вместо граней и площадей будут гиперповерхности и многомерные объемы. А утверждение, конечно, останется все тем же: сумма квадратов объемов боковых граней равна квадрату объема основания, — просто количество граней будет больше, а объем каждой из них станет равен половине произведения векторов-образующих. Вообразить это почти невозможно! Можно только, как говорят философы, помыслить!

Что удивительно, узнав о том, что такая теорема уже известна, я ничуть не расстроился. Где-то в глубине души я подозревал, что вполне возможно, я был не первый, и понимал, что нужно быть всегда к этому готовым. Но тот эмоциониальный опыт, который я получил, зажег во мне искру исследователя, которая, я уверен, теперь уже не угаснет никогда!

Эрудированный читатель в комментариях прислал ссылку
Теорема де Гуа

Выдержка из Википедии

В 1783 году теорема была представлена Парижской академии наук французским математиком Ж.-П. де Гуа, однако ранее она была известна Рене Декарту[3] и до него Иоганну Фульгаберу (англ.), который, вероятно, первым открыл её в 1622 году[4]. В более общем виде теорему сформулировал Шарль Тинсо (фр.) в докладе Парижской академии наук в 1774 году[4]

Так что я опоздал не на 18 лет, а как минимум на пару веков!

Источники

Читатели указали в комментариях несколько полезных ссылок. Вот эти и некоторые другие ссылки:

Источник

Египетский треугольник

Автор: admin · 8 апреля, 2014

Египетский треугольник.

Название «египетский треугольник» появилось уже в 5 веке до н.э. Принадлежит оно прямоугольному треугольнику, стороны которого равны соответственно 3, 4 и 5.

Назван он был так потому, что очень широко применялся еще в Древнем Египте в различных сферах жизнедеятельности.

Хотя уже тогда он был знаком людям далеко за пределами Древнего Египта, но, видимо, его уникальные свойства заметили и начали использовать впервые именно там.

В чем же состоит его отличительная особенность?

Во-первых, все его стороны и площадь — это целые числа;

во-вторых, сумма квадратов катетов равна квадрату гипотенузе ( а это ведь теорема Пифагора, которую все знают со школы! Но о Пифагоре чуть позже);

в-третьих, это то, что с его помощью можно отмерять прямые углы в пространстве (треугольник-то прямоугольный!), а это просто необходимо, например, в строительстве;

и, в-четвертых, этот треугольник можно запросто построить с помощью простой веревки.

А теперь про Пифагора. Египетский треугольник тесно связан с его именем.

Возможно, изучение интересных особенностей египетского треугольника и подтолкнуло Пифагора на попытку обобщения зависимостей во всех других прямоугольных треугольниках. Что ему, как известно, удалось!

Кстати, оказывается, теорема Пифагора попала в Книгу Рекордов Гиннеса как теорема с самым большим количеством доказательств (их насчитывается около 500).

Источник