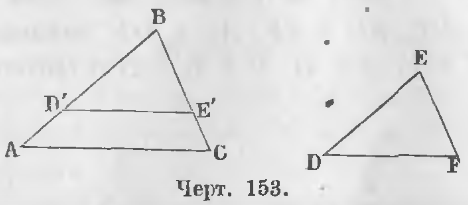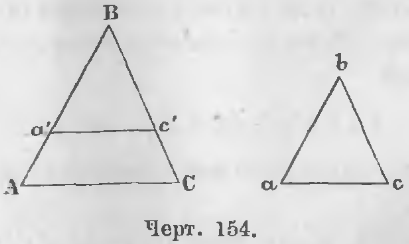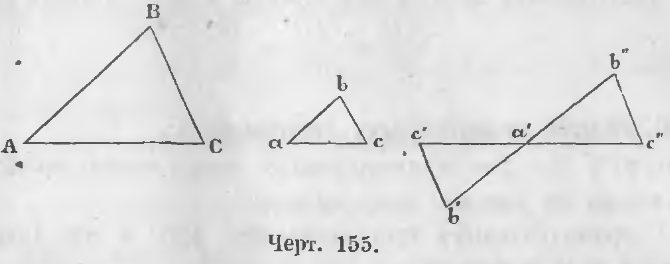Как доказать что треугольники подобны в параллелограмме
Как доказать что треугольники подобны в параллелограмме
Признака подобия треугольников
Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F
F’`. Напомним, что запись подобия треугольников `Delta ABC
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC
Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,
`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.
Два треугольника подобны, если:
1. два угла одного соответственно равны двум углам другого;
2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
3. три стороны одного треугольника пропорциональны трём сторонам другого.
В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.
Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.
Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.
И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.
Delta COB` по двум углам (рис. 10б):
`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.
3. Учитывая, что `BD = BO + OD` находим отношение
`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.
Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.
Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.
Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.
Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.
Попытайтесь доказать это самостоятельно.
Прямоугольные треугольники подобны, если:
1. они имеют по равному острому углу;
2. катеты одного треугольника пропорциональны катетам другого;
3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.
Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.
Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.
СВОЙСТВА ВЫСОТ И БИССЕКТРИС
Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C
Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).
Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).
В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.
Таким образом, `Delta A_1 B_1 C
$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos C =b \cos C;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos C =a \cos C,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC,$$
коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.
$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos\varphi =b |\cos C|;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos\varphi =b |\cos C|,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC$$
с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.
В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).
Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).
Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).
По первой лемме о высотах `Delta A_1 B_1 C
Delta ABC`, `/_ A_1 B_1 C = /_ B`.
Аналогично `Delta AB_1C_1
Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.
Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.
Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.
Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.
Установим ещё одно свойство биссектрисы угла треугольника.
Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.
По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.
Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16
Математика
В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).
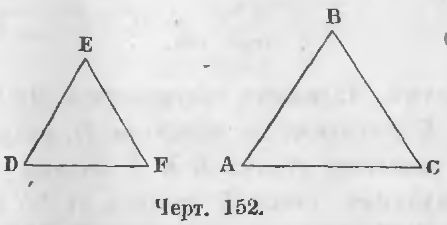
В треугольниках ABC и DEF (черт. 152), в которых
стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.
Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.
Если в двух треугольниках (черт. 152) ABC и DEF углы равны
и соответственные стороны пропорциональны
то треугольники называются подобными.
Подобие обычно выражают знаком ∼.
Подобие двух треугольников изображают письменно:
Случаи подобия треугольников
Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.
Дано. В треугольниках ABC и DEF углы равны (черт. 153).
Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:
Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,
Если соответственные углы равны, то D’E || AC.
По теореме 86 имеют место равенства
Так как BD’ = ED, BE’ = EF, D’E’ = DF, то
AC/DF = AB/ED = BC/EF (ЧТД).
Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.
Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).
то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).
Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.
Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.
Требуется доказать, что треугольники подобны.
Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆ BD’E’ = ∆ DEF, следовательно,
Так как имеет место пропорция
то сторона D’E’ || AC (теорема 87).
т. е. три угла одного равны трем углам другого треугольника.
В этом же случае треугольники ABC и DEF подобны (ЧТД).
Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.
Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:
AB/ab = BC/bc = AC/ac (1)
Требуется доказать, что у них углы равны, т. е.
Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:
Так как Ba’ = ba, то рядом с этими имеют место отношения:
AB/ab = BC/Bc’ = AC/a’c’ (2)
Сопоставляя отношения (1) и (2), заключаем, что
следовательно, два треугольника a’Bc’ и abc равны, откуда
∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c
∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,
следовательно, углы двух треугольников ABC и abc равны (ЧТД).
Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.
Доказательство. Здесь могут быть два случая:
1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.
2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.
AB || a’b’, AC || a’c’, BC || b’c’.
Углы же между параллельными сторонами обращены в разные стороны.
В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.
Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,
a’b»c», следовательно, ∆ ABC
a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’
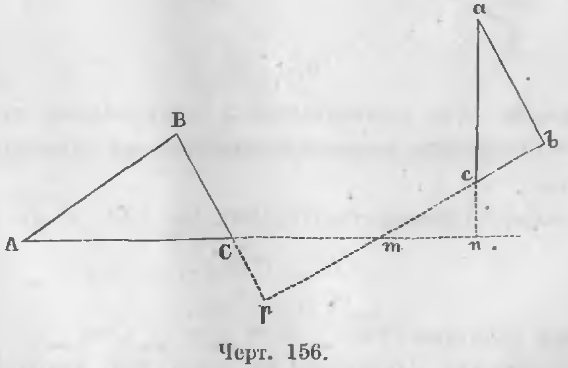
Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.
Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:
ab ⊥ AB, ac ⊥ AC, bc ⊥ BC
Требуется доказать, что треугольники подобны.
Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо
Углы при точке m равны как вертикальные,
а следовательно, и третьи углы равны ∠pCm = ∠mcn.
Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция
Подобие прямоугольных треугольников
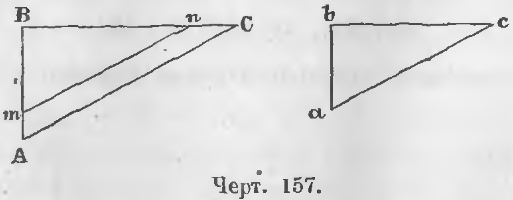
Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.
Требуется доказать, что треугольники ABC и abc подобны.
Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).
Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.
Дано. В прямоугольных треугольниках ABC и abc (черт. 157)
Требуется доказать, что ∠A = ∠a, ∠C = ∠c.
Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:
Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.
Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:
следовательно, два треугольника ABC и abc подобны.
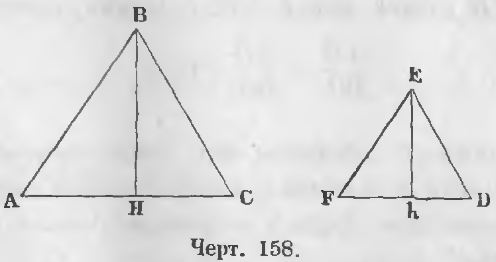
Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.
Даны два подобных треугольника ABC и FED (черт. 158), следовательно,
∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF
и проведены высоты BH и Eh.
Требуется доказать, что AB/FE = BH/Eh.
Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,
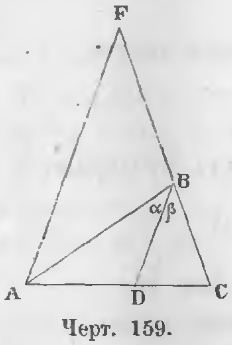
Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.
Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).
∠ABD = ∠DBC или ∠ α = ∠ β
Требуется доказать, что AB/BC = AD/DC.
Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA
∠AFB = ∠ β как соответственные углы,
∠FAB = ∠ α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.
Так как ∠ α = ∠β по условию, то
∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.
Из того, что AF || BD вытекает пропорция:
Заменяя FB равным отрезком AB, получим пропорцию:
Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.
Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:
Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:
Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,
Так как ∠ α = ∠ FAB, ∠β = ∠ AFB, то и
Отношения в прямоугольном треугольнике
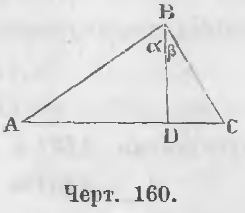
Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.
Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.
Требуется доказать, что AD/BD = BD/DC.
Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠ α = d, ∠ α + ∠β = d вытекает
A + α = α + β, или A = β, следовательно и C = α.
Из подобия треугольников ABD и BDC вытекает пропорция
Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.
Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ ABC = ∠ADB как прямые, ∠A общий, следовательно,
Из подобия треугольников вытекает пропорция:
b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,
∠A = ∠ β, откуда
DC/BC = BC/AC (b)
Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.
Из предыдущих пропорций (a) и (b) вытекают равенства:
AB 2 = AD · AC
BC 2 = DC · AC
Складывая их, получим:
a) Гипотенуза равна корню квадратному из суммы квадратов катетов.
b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.
Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.
Дано. В квадрате ABCD проведена диагональ AC (черт. 161).
Требуется доказать, что отношение AC/AD есть величина несоизмеримая.
Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.
a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо
Соотношение между сторонами остроугольного и тупоугольного треугольника
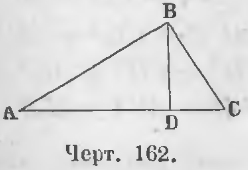
Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.
Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.
Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.
Доказательство. Для прямоугольного треугольника ABD имеем равенство:
Из прямоугольного треугольника BDC имеем:
Вставляя величины BD 2 и AD 2 в равенство (a), получим:
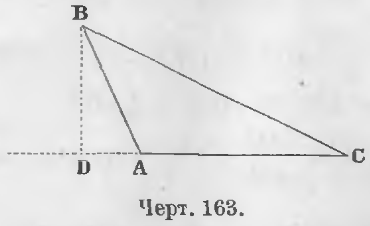
2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.
Доказательство. Из прямоугольного треугольника ABD имеем:
Из прямоугольного треугольника BCD имеем:
Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.
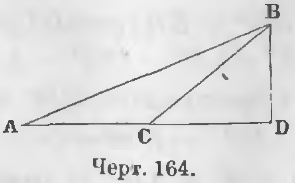
Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.
Требуется доказать, что
AB 2 = AC 2 + BC 2 + 2AC · CD
Доказательство. Из тупоугольного треугольника ABC имеем:
AB 2 = BD 2 + AD 2 (a)
AD = AC + CD, AD 2 = AC 2 + CD 2 + 2AC · CD
Из прямоугольного треугольника BCD вытекает, что
Заменяя AD 2 и BD 2 в равенстве (a), получим:
AB 2 = BC 2 + AC 2 + 2AC · CD (ЧТД).
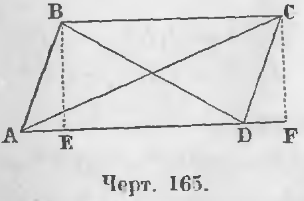
Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.
Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.
Требуется доказать, что
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:
Из тупоугольного треугольника ACD равенство:
AC 2 = CD 2 + AD 2 + 2AD · DF (2)
Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.
Сложив равенства (1) и (2), имеем:
BD 2 + AC 2 = AB 2 + AD 2 + CD 2 + AD 2
BD 2 + AC 2 = AB 2 + BC 2 + CD 2 + AD 2 (ЧТД).
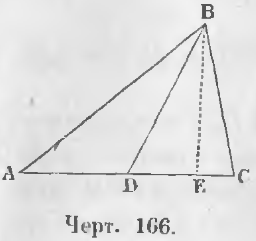
Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.
Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).
Требуется доказать, что
AB 2 + BC 2 = 2AD 2 + 2BD 2
Доказательство. Проведем высоту BE.
Из прямоугольных треугольников ABE и BCE вытекают равенства:
AB 2 = BE 2 + AE 2
BC 2 = BE 2 + CE 2
AB 2 + BC 2 = 2BE 2 + AE 2 + CE 2 (a)
AE 2 + CE 2 = 2CD 2 + 2DE 2 (b)
Заменяя в равенстве (a) сумму AE 2 + CE 2 из равенства (b), имеем:
Из прямоугольного треугольника BDE видно, что
Параллелограмм: свойства и признаки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.