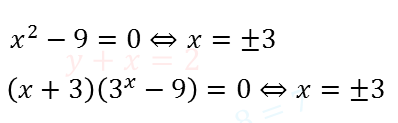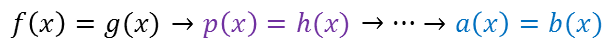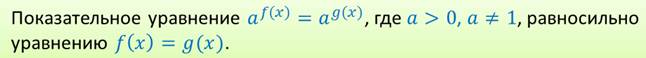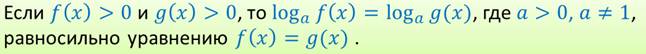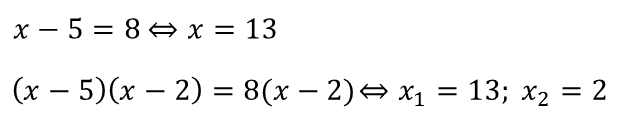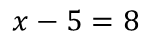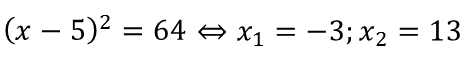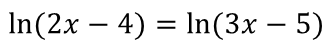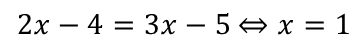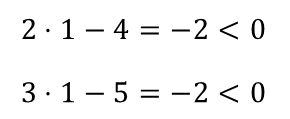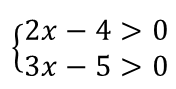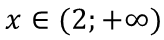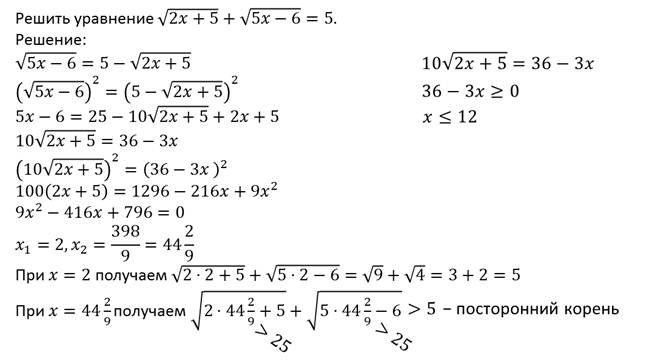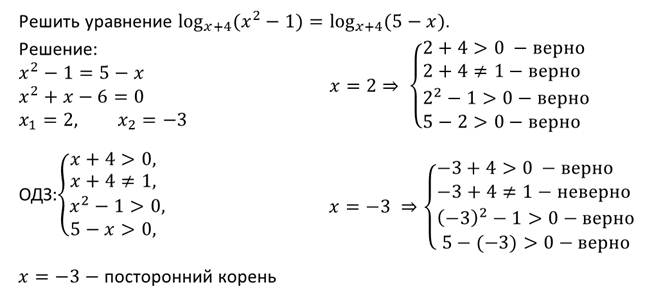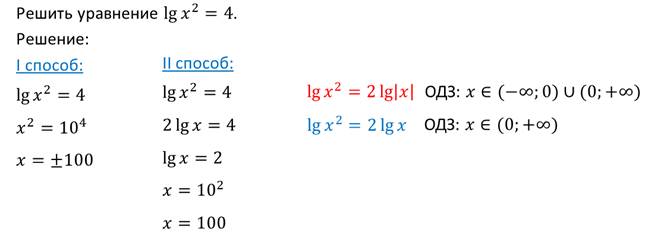Как доказать что уравнения равносильны
Равносильные уравнения. Равносильные преобразования уравнений
Равносильными называют уравнения, имеющие одни и те же корни. Равносильными считаются также уравнения, каждое из которых не имеет корней.
Основные равносильные преобразования уравнений:
Умножение или деление обеих частей уравнения на одно число или выражение не равное нулю.
Применение всех формул и свойств, которые есть в математике.
Равносильные уравнения и уравнения следствия
Равносильные преобразования уравнений можно назвать «правильными» или «безошибочными» преобразованиями, потому что, сделав их, вы не нарушите математических законов. Почему тогда математики так их и не назвали: «правильные преобразования уравнений»? Потому что есть еще «полу-правильные» преобразования уравнений. В них уравнение при преобразовании приобретает дополнительные корни по ходу решения, но лишние корни мы при записи ответа не учитываем. Строгие математики их называют уравнениями следствиями:
Если каждый корень первого уравнения является корнем второго уравнения, но при этом у второго также есть корни не подходящие первому, то второе уравнение является следствием второго.
Пример (ОГЭ). Решите уравнение \(x^2-2x+\sqrt<2-x>=\sqrt<2-x>+3\)
Перенесем оба слагаемых из правой части в левую.
Взаимно уничтожим подобные слагаемые. Это и есть «полу-правильное преобразование», так как после него у уравнения становится два корня вместо изначального одного.
Сверяем корни с ОДЗ и исключаем неподходящие.
\(↑\) не подходит под ОДЗ
Пример. В каких пунктах применялись равносильные преобразования, а в каких был переход к уравнению следствию? Укажите какие виды равносильных преобразований применялись.
В пункте a) применялось равносильное преобразование 1.
В пункте b) перешли к уравнению следствию, так как \(\sqrt
В пункте с) тоже перешли к уравнению следствию, из-за того что умножили на знаменатель;
В пункте d) применялось равносильное преобразование: «Извлечения корня нечетной степени из обеих частей уравнения»;
В пункте e) умножили обе части уравнения на \(2\) т.е. равносильно преобразовали;
В пункте f) перешли от вида \(a^
Равносильные уравнения, преобразование уравнений
Некоторые преобразования позволяют нам перейти от решаемого уравнения к равносильным, а также к уравнениям-следствиям, благодаря чему упрощается решение первоначального уравнения. В данном материале мы расскажем, что из себя представляют эти уравнения, сформулируем основные определения, проиллюстрируем их наглядными примерами и поясним, как именно осуществляется вычисление корней исходного уравнения по корням уравнения-следствия или равносильного уравнения.
Понятие равносильных уравнений
Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.
Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.
Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.
Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.
Приведем несколько примеров таких уравнений.
Для наглядности рассмотрим несколько примеров неравносильных уравнений.
Определения, данные выше, подойдут и для уравнений с несколькими переменными, однако в том случае, когда мы говорим о двух, трех и более корнях, более уместно выражение «решение уравнения». Таким образом, подытожим: равносильные уравнения – это те уравнения, у которых одни и те же решения или их совсем нет.
Понятие уравнений-следствий
Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.
Следствием уравнения f ( x ) = g ( x ) будет уравнение p ( x ) = h ( x ) при условии, что каждый корень первого уравнения будет в то же время корнем второго.
1. Понятие уравнения и его корней
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной x записывают так: f (я) = g (я).
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны.
2х = —1 — линейное уравнение; х 2 — 3х + 2 = 0 — квадратное уравнение; чJx + 2 = x — иррациональное уравнение (содержит переменную под знаком корня).
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни (и обосновать, что других корней нет) или доказать, что корней нет.
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций f (x) и g (x), стоящих в левой и правой частях уравнения.
Для уравнения л/x + 2 = x ОДЗ: x + 2 1 0, то есть x 1 —2, так как область определения функции f (x) = yj x + 2 определяется условием: x + 2 1 0, а область определения функции g (x) = x — множество всех действительных чисел.
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения (см. пункт 5 этой таблицы).
► Возведем обе части уравнения в квадрат:
Понятно, что каждый корень данного уравнения принадлежит как области определения функции f (x), так и области определения функции g (x) (иначе мы не сможем получить верное числовое равенство). Поэтому каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях применить анализ ОДЗ уравнения при его решении.
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 7 на с. 54.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один о р и е н т и р: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 6. В пункте 3 этой таблицы приведено решение уравнения
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком ^, но его использование для записи решения не является обязательным. Вместе с тем, если этот значок записан, то это свидетельствует о том, что мы воспользовались уравнениями- следствиями, и поэтому обязательно в запись решения необходимо включить проверку полученных корней.
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 0).
В курсе алгебры и начал математического анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множе-
стве, если на этом множестве они имеют одни и те же корни, то
есть каждый корень первого уравнения является корнем второго
и, наоборот, каждый корень второго уравнения является корнем
первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения х + 3 = 0 и 2х + 6 = 0 — равносильные, поскольку оба имеют одинаковый корень х = —3 и других корней не имеют, таким образом, каждое из них имеет те же решения, что и второе.
При рассмотрении равносильности уравнений на множестве, которое отличается от множества всех действительных чисел, ответ на вопрос «Равносильны ли данные уравнения?» может существенно зависеть от того, на каком множестве мы рассматриваем эти уравнения. Например, если рассмотреть уравнения:
то, как было показано выше, уравнение (3) имеет единственный корень х = 1, а уравнение (4) — два корня: х = 1 и х = —1. Таким образом, на множестве всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень х = —1, которого нет у уравнения (3). Но на множестве положительных действительных чисел эти уравнения равно
сильны, поскольку на этом множестве уравнение (3) имеет единственный положительный корень х = 1 и уравнение (4) также имеет единственный положительный корень х = 1. Следовательно, на множестве положительных чисел каждое из этих уравнений имеет те же решения, что и второе.
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы). Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий.
По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и наоборот — каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму (с. 49).
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при
Например, чтобы решить с помощью равносильных преобразований урав-
——- = 0, достаточно учесть его ОДЗ: х + 1 Ф 0 и условие равенства
дроби нулю (дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю). Также следует обратить внимание на то, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлениях с сохранением правильности равенства.
Запись решения в этом случае может быть такой:
= 0. ► ОДЗ: х + 1 Ф 0. Тогда х 2 —1 = 0. Отсюда х = 1 (удовлетворяет
Получим х 2 — 6х = 0, х1 = 0, х2 = 6
к уравнению, ОДЗ которого шире, чем ОДЗ заданного уравнения;
Приведение обеих частей уравнения к общему знаменателю (при сокращении знаменателя)
4 + 7 = 4 x + 2 x + 3 x 2 + 5x + 6 Умножим обе части уравнения на общий знаменатель всех дробей (х + 2)(х + 3).
Возведение обеих частей иррационального уравнения в квадрат
yj2x +1 =Vx. 2х + 1 = х,
б) выполнение преобразований, при которых происходит неявное умножение на нуль;
Умножение обеих частей уравнения на выражение с переменной
х 2 + х + 1 = 0. Умножим обе части уравнения на х —1.
(х — 1)(х 2 + х + 1) = 0. Получим х 3 — 1 = 0, х = 1
Как получить правильное (или полное) решение
Пример правильного (или полного) решения
при решении уравнения
х1 = 0 не является корнем заданного уравнения
Выполнить проверку подстановкой корней в заданное уравнение
► х 2 — 6х = 0, х1 = 0, х2 = 6. Проверка показывает, что х1 = 0 — посторонний корень, х2 = 6 — корень.
Ответ: 6. x + 2 x + 3 x 2 + 5x + 6
Явное или неявное сужение ОДЗ заданного уравнения, в частности выполнение преобразований, в ходе которых происходит неявное деление на нуль
1. Деление обеих частей уравнения на выражение с переменной
Поделив обе части уравнения на х, получим
2. Сложение, вычитание, умножение или деление обеих частей уравнения на выражение, ОДЗ которого уже, чем ОДЗ заданного уравнения
Если к обеим частям уравнения прибавить \[x, то получим уравнение
x 2 + yfx = 1 + yfx, у которого только один корень х = 1
Равносильность уравнений
Урок 28. Алгебра 11 класc
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Равносильность уравнений»
• обобщить сведения о равносильности уравнений;
• повторить основные теоремы равносильности;
• рассмотреть причины потери и появления посторонних корней при решении уравнений.
В процессе изучения математики, начиная с младших классов, мы постоянно сталкиваемся с уравнениями с одной или двумя переменными, с неравенствами, с системами уравнений или неравенств. На сегодняшнем уроке мы постараемся обобщить все, что мы знаем об уравнениях.
Начнем с определения.
Два уравнения с одной переменной f(x) = g(x) и p(x) = h(x) называют равносильными, если множества их корней совпадают.
Другими словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.
Дадим еще одно определение.
Если каждый корень уравнения f(x) = g(x) является в то же время корнем уравнения p(x) = h(x), то уравнение p(x) = h(x) называют следствием уравнения f(x) = g(x).
Очевидно, что справедливо следующее утверждение: два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.
Таким образом, общую схему можно описать так. Исходное уравнение преобразовывается в более простое уравнение, полученное уравнение преобразовывается в еще более простое уравнение и так происходит до тех пор, пока не получится довольное простое уравнение, корни которого и находят.
Естественно возникает вопрос, а будут ли корни решенного простого уравнения корнями нашего исходного уравнения? Если все преобразования были равносильными, то есть все полученные уравнения равносильные, тогда да. Если же некоторые преобразования были равносильными, а в некоторых мы не уверены, но точно знаем, что переходили с их помощью к уравнениям-следствиям, то однозначного ответа на вопрос мы не получим.
Для того, чтобы на данный вопрос ответить точно, нужно все найденные корни проверить, подставив их в исходное уравнение. Если найденный корень последнего уравнения не удовлетворяет исходному уравнению, то его называют посторонним корнем и в ответ его включать не надо.
Как правило, решение уравнения осуществляется в три этапа.
1. Технический. На этом этапе осуществляется преобразование по схеме, которую мы описали выше.
2. Анализ решения. На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными.
3. Проверка. Если анализ, проведенный на втором этапе, показывает, что некоторые преобразования могли привести к уравнению-следствию, то обязательно проверка всех найденных корней их подстановкой в исходное уравнение.
Давайте теперь определимся: как же узнать, является ли переход от одного уравнения к другому равносильным преобразованием?
Попробуем вспомнить все теоремы, в которых уравнение заменяется равносильным уравнением. Эти теоремы были доказаны нами ранее, поэтому мы просто напомним их.
Теорема 1. Если какой-либо компонент уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Теорема 2. Если обе части уравнения возвести в одну и ту же нечетную степень, то получится уравнение, равносильное данному.
Теперь давайте вспомним, что областью определения уравнения эф от икс равно жэ от икс или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной икс, при которых одновременно имеют смысл выражения f(x) и g(x).
Теорема 4. Если обе части уравнения f(x) = g(x) умножить на одно и тоже выражение h(x, которое: имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x) = g(x); нигде в этой области не обращается в ноль, то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному.
Следствием этой теоремы будет известный факт о том, что если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильно данному.
Теперь давайте вспомним, какие преобразования переводят уравнение в уравнение-следствие.
Если в процессе решения, мы воспользуемся последними теоремами, но не будем проверять выполнение необходимых условий, то получится уравнение-следствие.
Второй корень является посторонним для уравнения:
А появился он потому, что мы умножили обе части уравнения на одно и то же выражение, нарушив при этом условие теоремы 4.
В этой теореме содержится требование: выражение, на которое мы умножаем обе части уравнения, нигде не должно обращаться в ноль. А в нашем случае, выражение x – 2 обращается в ноль при x = 2, которое и оказалось посторонним корнем.
Теперь давайте обе части исходного уравнения возведем в квадрат. Получим:
Посторонний корень появился потому, что мы возвели обе части уравнения в одну и ту же четную степень, нарушив при этом условие теоремы пять. В этой теореме содержится требование: обе части уравнения должны быть неотрицательны. Про выражение x – 5 мы не можем этого утверждать.
Потенцируя, получим уравнение
Но этот корень является посторонним для исходного уравнения, поскольку оба выражения под знаками логарифмов принимают отрицательные значения.
А появился этот корень потому, что при потенцировании, мы нарушили условие шестой теоремы. В этой теореме содержится требование: выражения под знаками логарифмов должны быть положительными, о выражениях 2x – 4 и 3x – 5 этого утверждать мы не можем, так как они при одних значениях x положительны, при других – они отрицательны.
В нашем примере переход от логарифмического уравнения к уравнению 2x – 4 = 3x – 5 привел к расширению области определения уравнения.
Область определения логарифмического уравнения задается системой неравенств
решением которого будет промежуток
Областью определения уравнения 2x – 4 = 3x – 5 является множество всех действительных чисел. То есть у области определения логарифмического уравнения добавился луч от минус бесконечности до двух. В этом промежутке и находится корень уравнения x = 1.
Давайте попробуем сформулировать возможные причины расширения области определения уравнения:
1. Освобождение в процессе решения уравнения от знаменателей, содержащих переменную величину.
2. Освобождение в процессе решения уравнения от знаков корней четной степени.
3. Освобождение в процессе решения уравнения от знаков логарифмов.
Итак при решении уравнения обязательна проверка всех найденных корней, если:
1. Произошло расширение области определения уравнения.
2. Осуществлялось возведение обеих частей уравнения в одну и ту же четную степень.
3. Выполнялось умножение обеих частей уравнения на одно и то же выражение с переменной (имеющее смысл во всей области определения уравнения).
В рассмотренном примере, при проверке корней у нас были небольшие и несложные вычисления, а как же быть в случаях, когда проверка корней сопровождается значительными вычислительными трудностями? Существует несколько так называемых обходных путей проверки.
Например, при проверке корней в примере, мы не высчитывали значение левой части уравнения, а просто прикидывали чему равно получившееся выражение. Такая прикидка – один из обходных путей проверки.
Но этот корень можно было проверить и другим способом. Мы могли его проверить не по исходному уравнению, а по полученному в процессе преобразований уравнению-следствию.
Как правило, самый легкий путь проверки – по области определения исходного уравнения.
Каждый раз, при решении уравнений, явно выделять три этапа мы не будем. Но мысленно мы всегда такое разбиение будем делать.
Рассмотрим еще один пример.
Мы рассмотрели варианты, когда уравнение в процессе преобразований приобретает новые корни, но бывают случаи, когда уравнение теряет корни. Укажем причины потери корней при решении уравнений:
Можно сделать вывод, что применяя при решении уравнения какую-либо формулу, надо следить за тем, чтобы ОДЗ переменной для правой и левой частей формулы были одинаковыми.