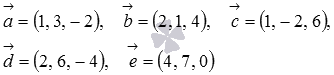Как доказать что вектора лежат в одной плоскости
Компланарность векторов. Условия компланарности векторов.
 |
| рис. 1 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Условия компланарности векторов
Примеры задач на компланарность векторов
Решение: найдем смешанное произведение векторов
Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.
Решение: найдем смешанное произведение векторов
Ответ: вектора компланарны так, как их смешанное произведение равно нулю.
Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования
 | 1 | 1 | 1 |  |
| 1 | 2 | 0 | ||
| 0 | -1 | 1 | ||
| 3 | 3 | 3 |
из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3
к 3-тей строке добавим 2-рую
Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.
Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.
Компланарные векторы
Что такое компланарные векторы
Векторы называются компланарными, если лежат в одной или параллельных плоскостях.
Это определение справедливо только для трех и более векторов, так как для двух направленных отрезков всегда можно найти плоскость, параллельную им.
Условия компланарности и линейная зависимость векторов
Среди условий компланарности векторов встречается понятие линейной зависимости, которое следует разобрать перед тем, как перейти непосредственно к условиям.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Линейная зависимость
Линейная комбинация — вектор, составленный из суммы векторов \(\overline
Существует пять критериев и свойств линейной зависимости векторов:
Условия компланарности
Для неограниченного числа векторов справедливо следующее: если среди них есть не более двух линейно независимых векторов, то они компланарны.
На практике чаще всего встречаются задачи с тройками векторов. Для них существуют и другие условия компланарности:
Теоремы, связанные с условием компланарности трех векторов
Правило, согласно которому три вектора компланарны, если их смешанное произведение равно нулю, проистекает из теоремы. Его также называют признаком и критерием компланарности векторов. Доказать данное утверждение можно следующим образом:
В то же время, результатом векторного произведения является вектор, перпендикулярный перемножаемым. Таким образом, векторы \overline a,\overline b,\overline c перпендикулярны одному и тому же вектору (\overline a\times\overline b), то есть лежат в параллельных плоскостях. Значит, векторы компланарны.
Для проверки, к доказательству данной теоремы можно подойти с другой стороны:
Пусть векторы \overline a,\overline b,\overline c компланарны.
Необходимо доказать, что их смешанное произведение \((\overline a\times\overline b)\cdot\overline c\) равняется нулю. Так как данные вектора компланарны, то \((\overline a\times\overline b)\) перпендикулярен каждому из них.
Отсюда следует, что его скалярное произведение с вектором \overline c будет равняться нулю. Это, в свою очередь, означает, что смешанное произведение \((\overline a\times\overline b)\cdot\overline c=0.\)
Пример задачи на компланарность векторов
Задача
Решение
Сперва необходимо построить на основе имеющихся точек векторы \(\overline
Чтобы проверить, принадлежать ли точки одной плоскости, необходимо найти смешанное произведение полученных векторов. Если оно равняется нулю, то векторы компланарны, следовательно, точки лежат в одной плоскости. В противном случае ответ на поставленный в условии вопрос будет отрицательным.
Смешанное произведение рассчитывается по формуле нахождения определителя матрицы:
Полученное число не равно нулю, следовательно, векторы некомпланарны. Это значит, что точки не лежат в одной плоскости.
Компланарные векторы и условие компланарности
В данной статье мы рассмотрим такие темы, как:
Определение компланарных векторов
Компланарные векторы — это векторы, которые параллельны одной плоскости или лежат на одной плоскости.
Два любых вектора всегда компланарны, поскольку всегда можно найти плоскости параллельные 2-м произвольным векторам.
Условия компланарности векторов
Примеры решения задач на компланарность векторов
Исследуем на компланарность векторы
Как решить?
Векторы будут являться компланарными, если их смешанное произведение равно нулю, поэтому вычисляем смешанное произведение заданных векторов. Для этого составляем определитель, по строкам которого записываются координаты векторов-сомножителей:
Отсюда следует, что смешанное произведение не равняется нулю, поэтому векторы не являются компланарными.
Ответ: векторы не являются компланарными.
Докажем, что три вектора
Как решить?
Находим смешанное произведение данных векторов:
Из данного примера видно, что смешанное произведение равняется нулю.
Ответ: векторы являются компланарными.
Проверим, компланарны ли векторы
Как решить?
Необходимо найти количество линейно независимых векторов: записываем значения векторов в матрицу и выполняем элементарные преобразования:
Из 2-ой строки вычитаем 1-ю, из 4-ой вычитаем 1-ю, умноженную на 3:
К 3-ей строке прибавляем 2-ю:
Поскольку в матрице только две ненулевые строки, делаем вывод, что среди них всего два линейно независимых вектора.
Ответ: векторы являются компланарными, поскольку среди них всего два линейно независимых вектора.
Компланарные векторы, исследование системы векторов на компланарность.
В этой статье мы поговорим о компланарности векторов. Сначала вспомним определение компланарности и получим необходимое и достаточное условие компланарности трех векторов в трехмерном пространстве. Далее разберемся с задачей исследования системы из n векторов на компланарность, рассмотрим решения характерных примеров.
Навигация по странице.
Необходимое и достаточное условие компланарности трех векторов.
Напомним определение компланарных векторов.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
А как же определить, являются ли три вектора компланарными?
Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.
Для компланарности трех векторов 
и 
трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Пусть 
, докажем что векторы и компланарны.
Так как 
, то векторы 
и перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор перпендикулярен и вектору 
и вектору 
. Следовательно, векторы и компланарны, так как перпендикулярны одному вектору .
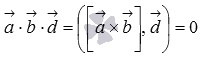
Пусть теперь векторы и компланарны, докажем равенство нулю смешанного произведения 
.
Так как векторы и компланарны, то вектор перпендикулярен каждому из них, следовательно, скалярное произведение вектора на равно нулю, что означает равенство нулю смешанного произведения .
Итак, теорема полностью доказана.
Покажем применение доказанного условия компланарности трех векторов к решению задач.
Компланарны ли векторы 
, заданные в прямоугольной системе координат.
Вычислим их смешанное произведение по координатам:
Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.
Необходимое и достаточное условие компланарности векторов можно использовать для проверки принадлежности четырех точек пространства А, В, С и D одной плоскости. Для этого находим координаты векторов 
и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.
Принадлежат ли точки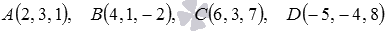 
одной плоскости?
Найдем координаты векторов (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца):
Теперь вычисляем смешанное произведение этих векторов
Так как смешанное произведение векторов отлично от нуля, то векторы не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.
Исследование системы векторов на компланарность, примеры и решения.
А как же быть, если требуется установить компланарность системы векторов, число векторов которой больше трех?
Давайте ответим на этот вопрос и получим условие компланарности системы из n векторов трехмерного пространства.
В предыдущем пункте мы показали, что для компланарности трех векторов и необходимо и достаточно равенство нулю их смешанного произведения: . Так как смешанное произведение трех векторов в координатной форме представляет собой определитель матрицы, строками которой являются координаты векторов и , то условие компланарности можно записать в виде 
. Вспомнив понятие ранга матрицы, последнее равенство можно интерпретировать следующим образом: ранг матрицы, строками которой являются координаты компланарных векторов и , меньше трех.
Обобщив последнее утверждение, мы получим необходимое и достаточное условие компланарности системы из n векторов трехмерного пространства: для компланарности системы из n векторов трехмерного пространства необходимо и достаточно, чтобы ранг матрицы, строками которой являются координаты векторов системы, был меньше трех.
Компланарны ли векторы
Составим матрицу, строками которой примем координаты данных векторов
Сразу легко отыскать минор второго порядка, отличный от нуля,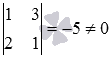 
.
Переберем окаймляющие его миноры третьего порядка:
Все они равны нулю, следовательно, ранг матрицы равен двум, поэтому, векторы заданной системы векторов компланарны в силу выполнения необходимого и достаточного условия компланарности.
Компланарные векторы
Вы будете перенаправлены на Автор24
Понятие компланарности векторов
Для начала рассмотрим, какие вектора называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Для дальнейшего рассмотрения напомним следующую теорему.
Теоремы, связанные с условием компланарности трех векторов
Если один из трех данных векторов можно разложить по двум другим векторам, то есть
Доказательство.
Здесь возможны два случая.
Теорема доказана.
Готовые работы на аналогичную тему
Доказательство.
\[\overrightarrow
Причем это разложение единственно.
Которое также единственно.
Теорема доказана.
Признак и критерий компланарности векторов
Рисунок 1. Условие компланарности векторов. Автор24 — интернет-биржа студенческих работ
Пример задачи
Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ
Решение.
Используя свойства сложения двух векторов, получим
Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.
Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Решение.
Применим признак компланарности трех векторов.
Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ
Следовательно, это векторы компланарны, ч. т. д.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 27 04 2021