Как доказать что векторы перпендикулярны через координаты

Как найти вектор, перпендикулярный вектору

Вы будете перенаправлены на Автор24

Понятие вектора и перпендикулярности векторов

Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Введем теперь, непосредственно, определение коллинеарных векторов.

Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).

Готовые работы на аналогичную тему

Также введем определение скалярного произведения, которое будет нам необходимо далее.

Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

Скалярное произведение также можно найти с помощью координат векторов следующим образом

$\overline<α>\overline<β>=α_1 β_1+α_2 β_2+α_3 β_3$

Признак перпендикулярности через пропорциональность

Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.

$\overline<α>\cdot \overline<β>=|\overline<α>||\overline<β>|cos⁡90^\circ =|\overline<α>||\overline<β>|\cdot 0=0$

По определению 6, будет верно равенство

Найдем скалярное произведение для этих векторов через формулу, данную выше

$\overline<α>\cdot \overline<β>=1\cdot 2+(-5)\cdot 1+2\cdot \frac<3><2>=2\cdot 5+3=0$

Значит, по теореме 1, эти вектор перпендикулярны.

Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение

Введем вначале понятие векторного произведения.

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Чтобы найти векторное произведение, будем пользоваться формулой

Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.

Найдем векторное произведение данных векторов.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 19 07 2021

Источник

Практическая работа по математике на тему «Коллинеарность и перпендикулярность векторов»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Определение коллинеарности и перпендикулярности векторов

Цель работы: при выполнении работы вы научитесь определять коллинеарность и перпендикулярность векторов, решать простейшие задачи с использованием определений и свойств.

При выполнении практической работы следует придерживаться следующих правил:

практическую работу следует выполнять в отдельной тетради для практических и домашних работ, чернилами любого цвета кроме красного, оставляя поля для рецензий;

решение задач должно располагаться в порядке возрастания их номеров, сохраняя нумерацию заданий;

перед решением каждой задачи нужно записать полностью её условие;

решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и выполняя необходимые чертежи.

Вектор – «направленный» отрезок. Векторы в прямоугольной системе координат задаются с помощью его координат.

Длиной ненулевого вектора называется длина отрезка АВ. Обозначается так: или ( ).

Вектор всегда можно получить из двух точек М(х ₁ ; у ₁ ; z ₁ ) и N (х ₂ ; у ₂ ; z ₂ ).

Для того чтобы проверить коллинеарность векторов, заданных своими координатами и надо проверить выполнение равенств:

Угол между двумя векторами можно всегда получить, отложив векторы от общей точки.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Для того чтобы проверить перпендикулярность векторов, заданных своими координатами и надо вычислить их скалярное произведение и далее проверить утверждение: скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны.

Задание 1. Постройте векторы и коллинеарные сонаправленные векторы.

Задание 3. Даны точки А(-2; 3; 1), В(-2; 1; 2) и С(0; 3; 4). Проверьте перпендикулярность векторов АВ и АС.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 1. Постройте векторы и коллинеарные противоположно направленные векторы.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 3. Даны точки А(0; 1; 2), В(; 2; 1), С(; 2; 1) и Д(0; 2; 1). Докажите, что АВСД – квадрат.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 3. Даны точки А(0; 1; 2), В(; 2; 1), С(; 2; 1) и Д(0; 2; 1). Докажите, что АВСД – квадрат.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1544282

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

МГУ откроет первую в России магистерскую программу по биоэтике

Время чтения: 2 минуты

Россияне чаще американцев читают детям страшные и печальные книжки

Время чтения: 1 минута

В МГПУ сформулировали новые принципы повышения квалификации

Время чтения: 4 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

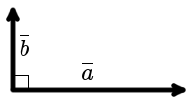
Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Как доказать что векторы перпендикулярны через координаты

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник