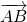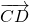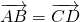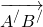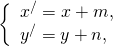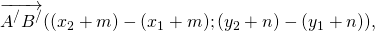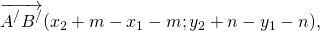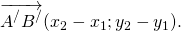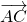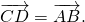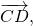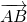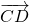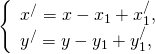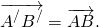Как доказать что векторы равны по координатам

Равные векторы

В различных школьных учебниках определение равных векторов даётся по-разному.

В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.

Два вектора называются равными, если они совмещаются параллельным переносом.

(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Например, изображенные на рисунке

Равенство векторов обозначают так:

(Свойства равных векторов)

1) Равные векторы сонаправлены и имеют равные длины.

2) Равные векторы имеют равные координаты.

3) От любой точки можно отложить вектор, равный данному, и притом только один.

1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.

2) Пусть дан вектор

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂).

По определению равных векторов, вектор

равный данному, получен из

Если этот параллельный перенос задан формулами

Найдём координаты каждого из векторов:

То есть координаты равных векторов

Что и требовалось доказать.

Таким образом, координаты задают длину и направление вектора, но не фиксируют его.

3) Пусть даны вектор

и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор

При таком параллельном переносе вектор

переходит в вектор

По определению равных векторов,

Что и требовалось доказать.

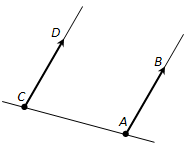
На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).

Например,

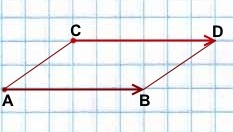
отложенный от точки C, равен вектору

(Признаки равенства векторов)

1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.

2) Если у векторов соответствующие координаты равны, то векторы равны.

1) Пусть векторы

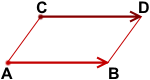
сонаправлены и имеют одинаковые длины.

Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор

переводит в вектор

По определению равных векторов,

Что и требовалось доказать.

Параллельный перенос, заданный формулами

переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы

А это означает, что

Что и требовалось доказать.

В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.

Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.

Источник

Как доказать что векторы равны по координатам

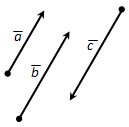
Вопрос 2. Какие векторы называются одинаково направленными (противоположно направленными)?
Ответ. Векторы \(\overline\) и \(\overline\) называются одинаково направленными, если полупрямые AB и CD одинаково направлены.
Векторы \(\overline\) и \(\overline\) называются противоположно направленными, если полупрямые AB и CD противоположно направлены.
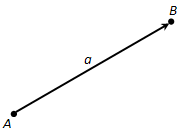
На рисунке 212 векторы \(\overline\) и \(\overline\) одинаково направлены, а векторы \(\overline\) и \(\overline\) противоположно направлены.

Вопрос 3. Что такое абсолютная величина вектора?
Ответ. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора \(\overline\) обозначается |\(\overline\)|.

Вопрос 4. Что такое нулевой вектор?
Ответ. Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулём с чёрточкой (\(\overline<0>\)). О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.

Вопрос 5. Какие векторы называются равными?
Ответ. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.

Вопрос 6. Докажите, что равные векторы одинаково направлены и равны по абсолютной величине. И обратно: одинаково направленные векторы, равные по абсолютной величине, равны.
Ответ. При параллельном переносе вектор сохраняет своё направление, а также свою абсолютную величину. Значит, равные векторы направлены одинаково и равны по абсолютной величине.
Пусть \(\overline\) и \(\overline\) – одинаково направленные векторы, равные по абсолютной величине (рис. 213). Параллельный перенос, переводящий точку C в точку A, совмещает полупрямую CD с полупрямой AB, так как они одинаково направлены. А так как отрезки AB и CD равны, то при этом точка D совмещается с точкой B, т.е. параллельный перенос переводит вектор \(\overline\) в вектор \(\overline\). Значит, векторы \(\overline\) и \(\overline\) равны, что и требовалось доказать.

Вопрос 7. Докажите, что от любой точки можно отложить вектор, равный данному вектору, и только один.
Ответ. Пусть CD – прямая, а вектор \(\overline\) – часть прямой CD. Пусть AB – прямая, в которую переходит прямая CD при параллельном переносе, \(\overline\) – вектор, в который при параллельном переносе переходит вектор \(\overline\), а значит, векторы \(\overline\) и \(\overline\) равны, а прямые AB и CD параллельны (см. рис. 213). Как мы знаем, через точку не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной (аксиома параллельных прямых). Значит, через точку A можно провести одну прямую, параллельную прямой CD. Так как вектор \(\overline\) – часть прямой AB, то через точку A можно провести один вектор \(\overline\), равный вектору \(\overline\).

переводит точку A₁ в точку A’₁, а точку A₂ в точку A’₂, т.е. векторы \(\overline1A₂>\) и \(\overline1A’₂>\) равны, что и требовалось доказать.

Источник

Как доказать что векторы равны по координатам

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник