Как доказать что заданная позиция в игре является выигрышной или проигрышной ответ

Урок 8
Использование графов
(§7. Системный подход в моделировании)

Содержание урока

Вопросы и задания

Вопросы и задания

1. Приведите примеры, когда в одной и той же ситуации люди используют разные модели. Какие из них можно считать системами?
2. Какие два типа табличных моделей вы знаете?
3. К какому типу можно отнести модель, построенную при решении задачи с путешественником? Обоснуйте ответ.
4. Какие типы диаграмм вы знаете? В каких случаях используется каждый из них?
*5. Изучите другие типы диаграмм, которые можно построить в табличных процессорах. Зачем они используются? Приведите примеры.
6. Объясните, почему любую систему, состоящую из подсистем, можно представить в виде иерархии.
7. Вспомните, что такое матрица смежности и весовая матрица графа (см. главу 1 в учебнике для 10 класса).
8. Зачем нужны сетевые модели при планировании производства?
9. Что такое семантические сети? В чем их достоинства и недостатки?
10. Что такое семантическая паутина? Можно ли её создать на основе существующих веб-страниц? Обоснуйте свой ответ.
11. Что такое выигрышная стратегия в игре?
12. Как доказать, что заданная позиция в игре является выигрышной (или проигрышной)? Как вы думаете, в каких случаях это сделать не удаётся?
13. Почему для того, чтобы доказать выигрыш какого-то игрока в заданной начальной позиции, не нужно строить полное дерево игры?

а) «Типы диаграмм»
б) «Сетевое планирование»
в) «Семантические сети»
г) «Интеллект-карты (mind maps)»
д) «Диаграммы Ганта»
е) «Использование ленты времени»

Следующая страница Задачи с 1 по 8

Cкачать материалы урока

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Игровые стратегии.

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§18. Игровые стратегии.

Выигрышные и проигрышные позиции

Ключевые слова:

Как вы уже знаете из § 16, игровые модели — это модели, которые описывают соперничество двух (или более) сторон, каждая из которых стремится к выигрышу, т. е. преследует свою цель. Часто цели участников противоречивы — выигрыш одного означает проигрыш других.

Построением и изучением игровых моделей занимается теория игр — раздел прикладной математики. Задача состоит в том, чтобы найти стратегию (алгоритм игры), который позволит тому или другому участнику получить наибольший выигрыш (или, по крайней мере, наименьший проигрыш) в предположении, что соперники играют безошибочно.

Стратегия — это алгоритм игры, который позволяет добиться цели в игре в предположении, что соперники играют безошибочно.

Мы будем изучать игры с полной информацией, в которых результат не зависит от случая (говорят, что в таких играх нет неопределённое™). Игроки делают ходы по очереди, в любой момент им известна позиция и все возможные дальнейшие ходы.

Можно ли считать играми с полной информацией «крестики-нолики», карточные игры, шахматы, шашки, «морской бой»?

Теоретически в играх с полной информацией можно построить последовательность ходов из заданной начальной позиции, которая приведёт одного из игроков к выигрышу или, по крайней мере, к ничьей. Нас будут интересовать простые игры, где не так много вариантов развития событий и перебор ходов возможен за приемлемое время. В большинстве игр, например в шахматах, количество вариантов настолько велико, что их полный перебор требует огромного времени и поэтому нереален.

Подсчитайте, сколько различных ходов могут сделать крестики в начале игры «крестики-нолики» на поле 3×3. Сколько различных позиций может возникнуть после ответного хода ноликов? После второго хода крестиков? После второго хода ноликов? Как можно сократить количество рассматриваемых вариантов в этой игре?

Подсчитайте, сколько различных ходов могут сделать белые в начале шахматной игры.

Все позиции (игровые ситуации) делятся на выигрышные и проигрышные.

Выигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку.

При этом говорят, что у него есть выигрышная стратегия — алгоритм выбора очередного хода, позволяющий ему выиграть.

Проигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, обязательно проиграет, если его соперник не сделает ошибку.

В этом случае говорят, что у него нет выигрышной стратегии. Таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника.

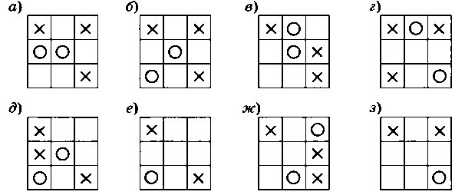
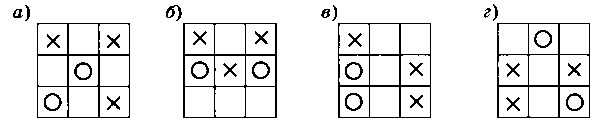
Найдите среди позиций игры в «крестики-нолики», показанных на рис. 3.37, выигрышные и проигрышные. Во всех случаях ходят нолики.

Рис. 3.37

Найдите все возможные ходы белых и чёрных фигур в позиции, показанной на рис. 3.38.

Рис. 3.38

Найдите выигрышный ход белых (они начинают).

Выигрышные и проигрышные позиции можно охарактеризовать так:

• позиция, из которой все возможные ходы ведут в выигрышные позиции, — проигрышная;
• позиция, из которой хотя бы один из возможных ходов ведёт в проигрышную позицию, — выигрышная, при этом выигрышная стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.

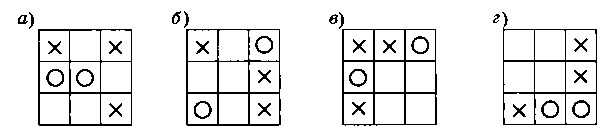
В позициях, показанных на рис. 3.39, найдите выигрышный ход ноликов, который создаёт проигрышную (для крестиков) позицию.

Рис. 3.39

Докажите, что все позиции, показанные на рис. 3.40, проигрышные для ноликов. Рассмотрите все возможные ходы и для каждого из них укажите выигрывающий ход крестиков.

Рис. 3.40

Дерево перебора вариантов

Одна из простых игр, где можно перебрать все варианты, — это игра с камнями. Перед двумя игроками лежит куча из некоторого количества камней (обозначим его S) или других одинаковых предметов (монет, бусин, пуговиц и т. п.) За один ход игрок может взять один или два камня. Тот, кто возьмёт последний камень, проигрывает.

Сыграйте в эту игру с соседом несколько раз для S = 6. Начинайте игру по очереди.

Для небольших значений S легко построить дерево перебора вариантов. Для S = 4 такое дерево показано на рис. 3.41.

Рис. 3.41

Буквой П обозначены ходы первого игрока (пусть его зовут Петя), а буквой В — ходы второго игрока (будем называть его Ваней). Числа в узлах дерева показывают количество камней в куче после очередного хода, а «-1» и «-2» — взятие из кучи соответственно одного или двух камней.

Очевидно, что позиция S = 1 — проигрышная: тот, кто ходит в этой позиции, проигрывает, потому что берёт последний (единственный) камень. Тогда выигрышными будут все позиции, из которых можно получить S = 1 каким-либо ходом — это позиции S = 2 и S = 3.

Из позиции S = 4 все возможные ходы ведут в выигрышные позиции S = 2 и S = 3, поэтому эта позиция проигрышная. Если Ваня не сделает ошибку, то Петя в любом случае проиграет.

Используя дерево перебора вариантов, выясните, какой ход должен сделать Ваня, чтобы выиграть в позиции S = 2? В позиции S = 3?

Выигрышную стратегию можно показать с помощью неполного дерева игры. Дело в том, что для выигрывающего игрока нам достаточно указать на каждом ходу один-единственный вариант, переводящий игру в проигрышную (для его соперника) позицию. А вот для проигрывающего игрока на каждом ходу нужно рассматривать все варианты, чтобы доказать, что он никак не может избежать поражения. Построим неполное дерево для начальной позиции S = 4, в которой, как мы показали, выигрышная стратегия есть у второго игрока (рис. 3.42).

Рис. 3.42

По этому дереву видно, что при любом своём первом ходе Петя обязательно проигрывает на втором ходу, взяв последний камень (если, конечно, Ваня не ошибётся).

Постройте дерево перебора вариантов для игры с камнями при S = 6. Выясните, какова начальная позиция — выигрышная или проигрышная. Почему? Постройте неполное дерево игры с доказательством стратегии выигрывающего игрока.

По результатам исследований определите, при каких значениях S начальные позиции будут выигрышными, а при каких — проигрышными. Если позиция выигрышная, какой стратегии должен следовать Петя?

Решение без дерева

Для того чтобы при заданном значении S определить, какова начальная позиция — выигрышная или проигрышная, не обязательно строить дерево. Составим таблицу, в которой для каждой позиции (для каждого значения S) будем указывать, какая это позиция и на каком ходу завершится игра. Как мы знаем, S = 1 — это проигрышная позиция, Петя проигрывает за один ход. Отмечаем её в таблице как П, где буква «П» означает проигрыш, а индекс «1» — количество ходов (рис. 3.43).

Рис. 3.43

Выигрышными будут все позиции, из которых можно каким-либо ходом получить проигрышную позицию S = 1, т. е. позиции S = 2 и S = 3. Отмечаем их как В, (выигрыш за 1 ход) — рис. 3.44.

Рис. 3.44

Из позиции S = 4 все возможные ходы ведут в выигрышные позиции, поэтому эта позиция — проигрышная (проигрыш за 2 хода) — рис. 3.45.

Рис. 3.45

Рассуждая таким же образом, заполните таблицу до конца.

Исследование игры

Исследуйте самостоятельно следующую игру.

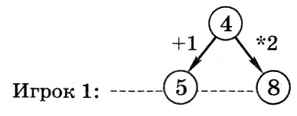
В игре участвуют два игрока, назовём их Петя (он ходит первый) и Ваня (второй). Вначале перед игроками лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу один камень (ход «+1») или увеличить количество камней в куче в два раза (ход «*2»). Например, имея кучу из 5 камней, за один ход можно получить кучу из 6 или 10 камней. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 14 камней или больше.

а) Определите, при каких значениях S Петя может выиграть первым ходом.

б) Определите, при каких значениях S Петя не может выиграть первым ходом, а Ваня выигрывает своим первым ходом. Заполните таблицу выигрышных и проигрышных позиций для всех значений S от 1 до 13.

в) Определите, при каких значениях S Ваня не всегда может выиграть своим первым ходом, но у него есть стратегия, следуя которой он выигрывает своим первым или вторым ходом.

г) Постройте неполное дерево игры с доказательством стратегии выигрывающего игрока при S = 4.

Выводы

• Стратегия — это алгоритм, который позволяет добиться цели в игре в предположении, что соперники играют безошибочно.
• Выигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку.
• Проигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, обязательно проиграет, если его соперник не сделает ошибку.
• Позиция, из которой все возможные ходы ведут в выигрышные позиции, — проигрышная.
• Позиция, из которой хотя бы один из возможных ходов ведёт в проигрышную позицию, — выигрышная, при этом выигрышная стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Что такое выигрышная стратегия в игре?

2. Как доказать, что заданная позиция в игре является выигрышной (или проигрышной)? Как вы думаете, в каких случаях это сделать не удаётся?

3. Почему для того, чтобы доказать выигрыш какого-то игрока в заданной начальной позиции, не нужно строить полное дерево игры?

4. Выполните по указанию учителя задания в рабочей тетради.

Источник

Урок 11
Использование графов
(§7. Системный подход в моделировании)

Содержание урока

Игровые стратегии

Игровые стратегии

Как вы уже знаете из § 6, игровые модели — это модели, которые описывают соперничество двух (или более) сторон, каждая из которых стремится к выигрышу, т. е. преследует свою цель. Часто цели участников противоречивы — выигрыш одного означает проигрыш других.

Построением и изучением игровых моделей занимается теория игр — раздел прикладной математики. Задача состоит в том, чтобы найти стратегию (алгоритм игры), который позволит тому или другому участнику получить наибольший выигрыш (или, по крайней мере, наименьший проигрыш) в предположении, что соперники играют безошибочно.

Во многих простых играх, в которых игроки ходят по очереди, есть не так много вариантов развития событий, и их можно рассмотреть полностью, однозначно определив, кто выиграет в заданной начальной ситуации, если оба соперника не будут ошибаться.

Все позиции (игровые ситуации) делятся на выигрышные и проигрышные. Выигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если сам не сделает ошибку. При этом говорят, что у него есть выигрышная стратегия — алгоритм выбора очередного хода, позволяющий ему выиграть.

Если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник. В этом случае говорят, что у него нет выигрышной стратегии. Таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника.

Выигрышные и проигрышные позиции можно охарактеризовать так:

• позиция, из которой все возможные ходы ведут в выигрышные позиции, — проигрышная;
• позиция, из которой хотя бы один из возможных ходов ведёт в проигрышную позицию, — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.

Для примера рассмотрим игру с камнями, в которой участвуют два игрока. Вначале перед игроками лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу один камень (ход «+1») или увеличить количество камней в куче в два раза (ход «*2»). Например, имея кучу из 5 камней, за один ход можно получить кучу из 6 или 10 камней. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 14 камней или больше.

Здесь «В₁» обозначает выигрыш за один ход.

При S = 6 у первого игрока есть два хода: ход «+1» даёт кучу из 7 камней, а ход «*2» — кучу из 12 камней. Выиграть за один ход он не может, оба возможных хода ведут в выигрышные (для второго!) позиции, поэтому первый игрок проиграет, если второй не ошибётся. Позицию S = 6 отметим в таблице как «х₁» (проигрыш за 1 ход):

Вспомним, что задача игрока — перевести игру в проигрышную для соперника позицию. Если S = 5 или S = 3, первый игрок может получить (ходом «+1» или «*2» соответственно) кучу из 6 камней, т. е. создать проигрышную позицию. Этого достаточно для выигрыша, но выиграть можно только за 2 хода:

Рассуждая аналогично, выясняем, что позиция S = 4 — проигрышная, так как возможные ходы ведут в выигрышные позиции (соперник выиграет за 1 или за 2 хода). При S = 2 первый игрок может своим ходом «*2» перевести игру в проигрышную позицию (S — 4), поэтому он выиграет. А при S = 1 он проиграет, потому что может своим ходом получить только кучу из 2 камней:

Полученная таблица показывает результат игры первого игрока в том случае, если второй не будет ошибаться. Если игра начинается в проигрышной позиции, первый игрок проиграет, а если в выигрышной — его стратегия состоит в том, чтобы на каждом шаге своим ходом создавать проигрышную позицию для соперника.

Для полного исследования всех вариантов игры можно построить дерево, содержащее все возможные ходы. Предположим, что сначала в куче 4 камня (эта позиция будет корнем дерева). Тогда в результате первого хода может получиться куча из 5 или 8 камней:

Следующий уровень дерева показывает все возможные позиции после ответного хода второго игрока:

Мы видим, что второй игрок может выиграть своим первым ходом (получив 16 камней), если первый построит кучу из 8 камней. В остальных случаях игра продолжается, и дерево можно строить дальше по тому же принципу.

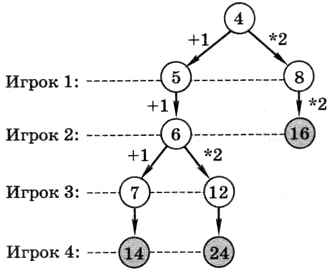
Как мы уже показали ранее с помощью таблицы, при S = 4 выигрывает второй игрок. Чтобы доказать это с помощью дерева, не нужно строить полное дерево игры. Достаточно рассмотреть все возможные ходы соперника и для каждого из них найти один (!) выигрышный ход второго игрока. Вариант с выигрышем в один ход мы уже разобрали, теперь посмотрим, что произойдёт, если первый игрок получит кучу из камней.

Как следует из построенной выше таблицы, для кучи из 5 камней выигрышный ход второго игрока — «+1», он переводит игру в проигрышную позицию. При любом ответе первого игрока второй выигрывает своим вторым ходом «*2»:

Таким образом, мы доказали, что при S = 4 у второго игрока есть стратегия, позволяющая ему гарантированно выиграть, по крайней мере, за 2 хода.

Следующая страница Вопросы и задания

Cкачать материалы урока

Источник

Урок 29
Использование графов
§ 18. Игровые стратегии

Содержание урока

Выигрышные и проигрышные позиции

Выигрышные и проигрышные позиции

Ключевые слова:

Как вы уже знаете из § 16, игровые модели — это модели, которые описывают соперничество двух (или более) сторон, каждая из которых стремится к выигрышу, т. е. преследует свою цель. Часто цели участников противоречивы — выигрыш одного означает проигрыш других.

Построением и изучением игровых моделей занимается теория игр — раздел прикладной математики. Задача состоит в том, чтобы найти стратегию (алгоритм игры), который позволит тому или другому участнику получить наибольший выигрыш (или, по крайней мере, наименьший проигрыш) в предположении, что соперники играют безошибочно.

Стратегия — это алгоритм игры, который позволяет добиться цели в игре в предположении, что соперники играют безошибочно.

Мы будем изучать игры с полной информацией, в которых результат не зависит от случая (говорят, что в таких играх нет неопределённое™). Игроки делают ходы по очереди, в любой момент им известна позиция и все возможные дальнейшие ходы.

Можно ли считать играми с полной информацией «крестики-нолики», карточные игры, шахматы, шашки, «морской бой»?

Теоретически в играх с полной информацией можно построить последовательность ходов из заданной начальной позиции, которая приведёт одного из игроков к выигрышу или, по крайней мере, к ничьей. Нас будут интересовать простые игры, где не так много вариантов развития событий и перебор ходов возможен за приемлемое время. В большинстве игр, например в шахматах, количество вариантов настолько велико, что их полный перебор требует огромного времени и поэтому нереален.

Подсчитайте, сколько различных ходов могут сделать крестики в начале игры «крестики-нолики» на поле 3×3. Сколько различных позиций может возникнуть после ответного хода ноликов? После второго хода крестиков? После второго хода ноликов? Как можно сократить количество рассматриваемых вариантов в этой игре?

Подсчитайте, сколько различных ходов могут сделать белые в начале шахматной игры.

Все позиции (игровые ситуации) делятся на выигрышные и проигрышные.

Выигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку.

При этом говорят, что у него есть выигрышная стратегия — алгоритм выбора очередного хода, позволяющий ему выиграть.

Проигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, обязательно проиграет, если его соперник не сделает ошибку.

В этом случае говорят, что у него нет выигрышной стратегии. Таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника.

Найдите среди позиций игры в «крестики-нолики», показанных на рис. 3.37, выигрышные и проигрышные. Во всех случаях ходят нолики.

Найдите все возможные ходы белых и чёрных фигур в позиции, показанной на рис. 3.38.

Найдите выигрышный ход белых (они начинают).

Выигрышные и проигрышные позиции можно охарактеризовать так:

• позиция, из которой все возможные ходы ведут в выигрышные позиции, — проигрышная;
• позиция, из которой хотя бы один из возможных ходов ведёт в проигрышную позицию, — выигрышная, при этом выигрышная стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.

В позициях, показанных на рис. 3.39, найдите выигрышный ход ноликов, который создаёт проигрышную (для крестиков) позицию.

Докажите, что все позиции, показанные на рис. 3.40, проигрышные для ноликов. Рассмотрите все возможные ходы и для каждого из них укажите выигрывающий ход крестиков.

Следующая страница Дерево перебора вариантов

Cкачать материалы урока

Источник

Задание 19, 20, 21 ЕГЭ информатика разбор «Анализ алгоритма логической игры»

Объяснение заданий 19, 20 и 21 ЕГЭ по информатике

19-е задание: «Анализ алгоритма логической игры»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.

Проверяемые элементы содержания: Умение анализировать алгоритм логической игры

20-е задание: «Поиск выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.

Проверяемые элементы содержания: Умение найти выигрышную стратегию игры

21-е задание: «Дерево игры для выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 10 минут.

Проверяемые элементы содержания: Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию

«Для пункта 2 или 3 в представленной стратегии рассмотрены не все возможные ходы проигрывающего игрока, которые он может сделать при игре выигрывающего игрока по выигрышной стратегии.
Для пункта 3 представлено дерево игры, содержащее лишние ветви, не относящиеся к выигрышной стратегии.
Дерево, являющееся частью ответа на пункт 3, представлено с использованием ссылок на
фрагменты, являющиеся решениями других пунктов задания.
В задании спрашивается, в частности, кто выиграет, а в ответе не указан в явном виде выигрывающий игрок. На все вопросы, поставленные в задании, должны быть даны чёткие ответы. Ответ на вопрос о выигрышной стратегии в стиле «Может выиграть первый игрок, но если он неправильно пойдёт, то выиграет второй» является ошибочным, поскольку выигрышная стратегия одного игрока не оставляет возможности победы другому игроку»

Теория игр. Поиск выигрышной стратегии

Для решения 19 задания необходимо вспомнить следующие темы и понятия:

проанализируем стратегию игры:

Ответ: при правильной игре (стратегии игры) выиграет первый игрок; для этого ему достаточно своим первым ходом убрать одну спичку.

Решение 19, 20, 21 заданий ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Игра с двумя кучами камней или табличка

Ответ: 14

Ответ: 24

Ответ: 23 25

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя.
За один ход игрок может убрать из одной из куч один камень или уменьшить количество камней в куче в два раза (если количество камней в куче нечётно, остаётся на 1 камень больше, чем убирается).

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 20 или меньше камней. В начальный момент в первой куче было 10 камней, во второй куче – S камней, S > 10.

Ответ: 22 44

Ответ: 24

Два игрока, Петя и Ваня, играют в следующую игру. На табличке написаны два значения. Оба игрока в свой ход могут заменить одно из значений на сумму обеих (по своему выбору). Первый ход делает Петя. Игра считается законченной когда сумма обеих значений равняется не меньше 56. То есть выигрывает игрок, получивший 56 или более в сумме. Начальное значение (10, S).

Задание 19 ЕГЭ.
Найдите максимальное S при котором Петя не может выиграть первым ходом.

Задание 20 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (9, 15).

Задание 21 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (3,7)? Опишите эту стратегию и изобразите дерево всех возможных партий при этой стратегии.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) два камня или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 44.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 44 или больше камней.

В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 38.
Задание 19 ЕГЭ.
При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?

Задание 20 ЕГЭ.
Назовите одно любое значение S, при котором Петя может выиграть своим вторым ходом.

Задание 21 ЕГЭ.
Назовите значение S, при котором Ваня выигрывает своим первым или вторым ходом.

✍ Решение:

Ответ 2: S = 16, 17 или 18 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)

Ответ 3: S = 14 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)

Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)

Игра с одной кучей камней

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 28.

Задание 19 ЕГЭ
а) Укажите такие значения числа S, при которых Петя может выиграть в один ход.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

Задание 20 ЕГЭ
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причем:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанных значений S опишите выигрышную стратегию Пети.

Задание 21 ЕГЭ
Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции

Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.

✍ Решение:

В таблице изображено дерево возможных партий (и только их) при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчеркнуты. На рисунке это же дерево изображено в графическом виде.

Дерево всех партий, возможных при стратегии Вани:

* красный круг означает выигрыш

Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в пять раз. Игра завершается в тот момент, когда количество камней в куче становится не менее 69.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 69 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 68.

Задание 19 ЕГЭ.
а) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.

б)Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.

Задание 20 ЕГЭ. Укажите 2 таких значения S, при которых у Паши есть выигрышная стратегия, причём Паша не может выиграть за один ход и может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.

Задание 21 ЕГЭ. Укажите хотя бы одно значение S, при котором у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы).

✍ Решение:

19.
а)S ≥ 14. При количестве камней в куче от 14 и выше Паше необходимо увеличить их количество в пять раз, тем самым получив 70 или более камней.

б) S = 13. Паша своим первым ходом может сделать 14, 17 или 65 камней, после этого Вася увеличивает количество в пять раз, получая 70, 85 или 325 камней в куче.

20. S = 9, 12. Для данных случаев Паше необходимо прибавить 4 камня к куче из 9 камней, либо 1 камень к куче из 12, и получить кучу из 13 камней.
После чего игра сводится к стратегии, описанной в пункте 1б.

21. S = 8. Своим первым ходом Паша может сделать количество камней в куче 9, 12 или 40. Если Паша увеличивает кол-во в пять раз, тогда Вася выигрывает своим первым ходом, увеличивая количество камней в пять раз.
Для случая 9 и 12 камней Вася использует стратегию, указанную в п.2.

Решение 19 задания смотрите на видео:

Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 7 камней, за один ход можно получить кучу из 14 или 8 камней. У каждого игрока, чтобы сделать ход, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 28. Если при этом в куче осталось не более 44 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 23 камня, и Паша удвоит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1≤ S ≤ 27.

Задание 19 ЕГЭ
а) При каких значениях числа S Паша может выиграть в один ход? Укажите все такие значения и соответствующие ходы Паши.
б) У кого из игроков есть выигрышная стратегия при S = 26, 25, 24? Опишите выигрышные стратегии для этих случаев.

Задание 20 ЕГЭ
У кого из игроков есть выигрышная стратегия при S = 13, 12? Опишите соответствующие выигрышные стратегии.

✍ Решение:

При S = 25 выигрышная стратегия есть у Паши. Удваивать количество камней нет смысла, т.к. количество превысит 44, значит, Паша добавит один камень, их станет 26, следующая Валя, — она может либо добавить камень (станет 27 камней, следующим ходом выиграет Паша) либо удвоить — и сразу проиграть, т.к. станет более 44 камней.

При S = 24 выигрышная стратегия есть у Вали. Паша делает ход первым: удваивать кучу нет смысла, т.к. в ней станет более 44, значит, Паша добавит один камень, их станет 25; следующая — Валя: она может только добавить один камень (станет 26 камней, следующим ходом Паша оказывается в проигрышной позиции, см. пункт при S = 26).

Дерево возможных партий:

Подробное объяснение 19 задания ЕГЭ смотрите на видео:

Игра с двумя кучами камней или табличка

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.

Задание 1.
Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание 2.
Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию.

Задание 3.
Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.

✍ Решение:

Видео решения 19 задания с двумя кучами:

Игра с набором слов

Петя и Ваня играют в игру: есть набор слов, необходимо последовательно называть буквы этих слов. Побеждает тот игрок, который называет последнюю букву любого слова из набора. Петя ходит первым.

Б) Даны 2 слова <ТРИТРИТРИ. ТРИ, РИТАРИТАРИТАРИТА. РИТА>. В первом слове 99 букв, во втором 164. Определить выигрышную стратегию.

Задание 2
Необходимо поменять две буквы местами из набора пункта 1А в слове с наименьшей длинной так, чтобы выигрышная стратегия была у другого игрока. Объяснить выигрышную стратегию.

Задание 3
Дан набор слов <Ворона, Волк, Волна, Производная, Прохор, Просо>. У кого из игроков есть выигрышная стратегия? Обосновать ответ и написать дерево всех возможных партий для выигрышной стратегии.

✍ Решение:

А) Для выигрыша Пете достаточно выбрать первую букву слова с нечетным количеством букв, тогда последний ход делает Петя. При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, что своим первым ходом он должен выбрать букву И (слово ИКЛМНИКЛМНХ из 11 букв). Ване придется выбрать букву К. Таким образом, они последовательно будут называть буквы первого слова, пока Петя не выберет последнюю букву Х. На этом игра закончится выигрышем Пети. При данной стратегии возможна только одна партия. Заключением партии будет написано слово ИКЛМНИКЛМНХ.

Б) При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, чтобы выбрать слово с нечетным количеством букв, т.к. при такой стратегии последнюю букву в любом случае записывает Петя. Т.о., Петя должен выбрать букву Т, т.к. в первом слове 99 букв.

Дерево возможных партий:

* Для Вани отображены только ходы по стратегии
** Красный круг означает выигрыш

Подробней с решением задания про слова ознакомьтесь в видеоуроке:

Источник