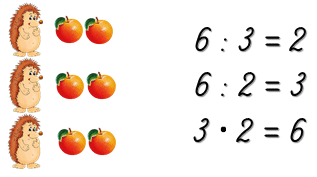Как объяснить ребенку что такое деление 3 класс
Как объяснить ребенку деление столбиком во 2-3 классе
Как объяснить ребенку деление столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.

Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
Как объяснить ребенку смысл действия «деление»?
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
Удобно показать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Как объяснить ребенку деление двузначного числа на однозначное не в столбик?
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
213:3
213 — делимое
3 — делитель
Рассуждаем так: 2 не делится на 3, значит — берем 21.
21 разделить на 3 — берем по 7.
7 умножить на 3 — получаем 21. Записываем.
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
Дальше можно взять пример посложнее, чтобы убедиться, что ребенок усвоил правильную запись и алгоритм рассуждений.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Предлагаем Вашему вниманию программы развивающих занятий с собаками- терапевтами в зависимости от возраста ребёнка и Ваших пожеланий:
Как научиться делить столбиком (уголком): примеры с решениями и объяснением
Азы деления столбиком и в уме дети изучают в начальной школе: в 3-м или 4-м классе. Но вникают в материал быстро и легко далеко не все третьеклассники. Дома нужно много практиковаться, решать тренировочные примеры. Но сначала лучше еще раз объяснить алгоритм действий, чтобы ребёнок смог понять, как деление уголком, с остатком, выявить пробелы в детских знаниях.
Как стать суперучителем без специальной подготовки и помочь ребенку с этой трудной темой, расскажем подробнее.
Из этой статьи вы узнаете
Как научиться делить столбиком
Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:
Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:
Смело предлагайте такие примеры:
Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.
На заметку! Все начальные математические навыки хорошо автоматизируются с помощью онлайн-тестов, где ребенок получает мгновенный результат своей работы.
Игровые задания
Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.
Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.
Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:
Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:
Ребенок должен найти дерево под номером 9.
Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:
1. Мама-учитель
2. Посмотреть вместе с ребенком обучающее видео

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.
3. Нанять репетитора
Деление (даже трёхзначных чисел на двузначные ) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.
Этот вариант оставим на крайний случай.
На заметку! Обязательно противопоставляйте деление умножению. Проверяйте результат обоих действий противоположным.
Как объяснить деление столбиком
Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.
Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:
Во время объяснения правил деления в столбик желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике.
Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.
На заметку! Приучайте малыша постоянно проверять себя. Школьник должен понимать, что величина остатка вычитания в столбике деления должен всегда быть меньше делителя.
Деление на однозначное число
Возьмите листок и ручку, посадите ребенка рядом. Сначала запишите пример уголком сами. Для деления на однозначное число выбирайте такие цифры, которые дают результат без остатка (полный ответ).
Первый урок по теме “Деление на однозначное число” можно построить так:
Для закрепления материала 3 класса запишите еще 3–5 примеров на деление на этом же листочке. Не отходите далеко от школьника, образец не прячьте, не превращайте урок в проверочную работу. Малыш только учится делить. На этом этапе помогайте ему, подсказывайте и наталкивайте на правильное решение для повышения уверенности в себе.
На заметку! Для автоматизации навыка деления столбиком можно составить небольшую памятку, где прописан каждый этап математического действия. Разрешайте школьнику смотреть в нее до тех пор, пока он сам не забудет об образце.
Деление на двузначное число
Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:
4070:74=55. Частное смотрим под уголком.
Для проверки правильности решение произведите умножение: 74х55=4070.
Есть мнение! Иметь в доме решебник с ГДЗ многие родители считают недопустимым. А зря. С помощью готовых заданий ребенок может легко проверить себя. Главное — правильно объяснить школьнику назначение сборника ДЗ с ответами.
Многозначные числа
Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:
При обучении решению задач с крупными ( многозначными ) числами действуйте поэтапно:
Найдите неполное частное в примерах: 369:28; 897:12; 698:36.
На заметку! Примеры с семизначными цифрами с третьеклассниками решать не нужно. Это лишнее. Достаточно остановиться на заданиях с пятизначными числами (до 10 000). Деление миллионов дети проходят в старших классах.
Деление с остатком
Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.
Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.
Урок может выглядеть так:
На заметку! Отделять целое число от остатка запятой, делать из него дробное на начальном этапе обучения делению не нужно. Записывайте остаток отдельно, чтобы школьник видел конечный результат разности в столбике.
Как объяснить ребенку деление?
Проблемы с математикой в начальной школе возникают исключительно из-за пробелов в знаниях.
Простые арифметические действия, такие как сложение и вычитание, должны выполняться автоматически — если ученик испытывает определенные трудности, то нужно сначала проработать эту тему, прежде чем приступать к более сложным операциям.
Как объяснить ребенку деление? Начать с азов, использовать игры и нестандартный подход.
Подготовка к обучению
Для начала стоит убедиться в том, что школьник усвоил предыдущую программу и ничто не помешает ему освоить текущую. Стоит проверить следующие знания:
числовые разряды (класс единиц и тысяч);
арифметические действия (сложение, вычитание);
Именно последний пункт является ключевым. Если в этом вопросе не возникает сложностей, то достаточно объяснить ребенку, что деление является противоположной умножению операцией. Соответственно, нужно провести аналогичные действия, но в обратном порядке.
Операция деления: основные обозначения
Очень часто в задачах вопрос сформулирован следующим образом: «Найти частное чисел 30 и 5» или «Определить делитель, если частное 42, а делимое — 7». Если ребенок не знает обозначений, то он не сможет приступить к решению такого примера. Поэтому начинать нужно с основ:
делимое — то число, которое и будет разделено;
делитель — число, на которое будет разделено делимое;
Понять роль каждого показателя поможет простая игра. Есть 12 вкусных конфет, а в семье 4 человека. Как разделить сладости поровну? Всего 12 — это делимое. Количество человек — делитель. Ученику начальной школы будет легче понять задачу, если объяснить ему, что делимое всегда самое большое число. Невозможно разделить 4 на 12, а значит, пример будет выглядеть следующим образом: 12:4 = 3.
Как понять суть деления?
На начальном этапе проще всего объяснить деление как операцию, противоположную умножению. Если ребенок безупречно знает таблицу, то он будет совершать действия на автомате:

Стоит «поиграть» с ассоциациями: разделить фрукты, шоколадки, конфеты между всеми членами семьи. Часто детям нравятся примеры с деньгами, построенные по принципу:
Было 28 гривен, купили 7 ручек, сколько стоит 1 ручка?
Такой подход позволит перейти от примеров на яблоках к работе непосредственно с числами.
Раскладываем число на компоненты
Работа с однозначными числами достаточно проста. Нужно выучить таблицу умножения и просто совершать действия в обратном порядке. Потребуется немного практики, чтобы научиться решать подробные примеры на скорость и в уме. Это будет полезно особенно при написании математических диктантов, когда учитель диктует задание, а детям нужно только записать правильный ответ.
Сложности наступают в тот момент, когда приходится решать примеры с теми числами, которые за пределами таблицы. Например:
Делимое — 90, делитель — 5. Нужно найти частное.
Ребенку сложно в уме выполнить требующиеся операции, поэтому нужно предложить ему разделить большое число на составляющие:
40:5 + 50:5 = 8+10=18; значит 90:5=18.
Если ученик в первом классе хорошо усвоил состав числа, то у него не возникнет сложностей и с похожими операциями: 72 — это 60+12, 84 — это 60+24, 93 — это 30+30+30+3.
Деление в столбик
Такой тип примеров — один из любимых у детей. Он используется при работе с трех- и двузначными числами, которые сложно разделить в уме. Последовательность действий следующая:

648|36; и начинаем подбирать значения, 36*2=72. 72 больше, чем 64, значит, этот вариант не подходит. 36*1=36, 36 меньше, чем 64 — это нужное нам число. Под 36 записываем 1. Продолжаем вести расчеты: 64-36=28, дописываем оставшееся число (648 — 64 мы уже использовали, осталось 8, которое мы и «сносим» к 28). Получается 288:36. Методом подбора определяем, что 36*10=360, 36*9=324, 36*8=288. Нужный результат получен, 288-288=0. Ответ:18.
Перепроверяем себя, выполнив умножение в столбик или используя устный счет: 36*18, действительно получается 648 — ответ верный, все действия были выполнены правильно.
Деление с остатком
К этим вычислениям нужно приступать только тогда, когда предыдущий материал выучен безупречно, алгоритм решения детально разобран и действия выполняются за считанные минуты. Как только ребенок детально разобрался в вопросе, можно двигаться дальше.
Особенность деления с остатком в том, что нужно выделить основную часть и понять, какое же число останется в итоге. На начальных порах у школьника может возникнуть барьер, ведь до этого все примеры решались легко, а теперь нужен иной подход к вычислениям.
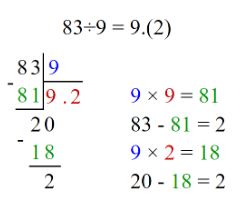
83:9, ребенок знает, что 81:9=9. 83-81=2. Значит, ответ: 9 и 2 в остатке.
114:5, 100:5=20, 10:5=2, 4 на 5 разделить невозможно. Соответственно, 114:5=100:5+20:5 и 4 = 22 и 4 в остатке.
Можно изучать этот тип примеров с помощью денежных операций, ведь сдача, полученная после оплаты покупок, — это как раз и есть остаток. Или же использовать для этой цели еду либо игрушки: куски торта, куклы можно делить на всех участников игрового процесса, подобрав такое количество, чтобы обязательно оставался «лишний» кусочек.
Дроби
Эта тема обычно является одной из самых сложных. А все потому, что школьникам сложно понять, почему 1 можно представить как 33 или 55. И хоть в школьной программе этому уделяется немало часов, многие ученики все-таки испытывают трудности. Деление простых чисел, операции в столбик, определение остатка — с этой задачей можно справиться и самостоятельно. Если же ученик «проседает» в дробях, то имеет смысл вернуться к истокам и повторно проработать простые арифметические действия.
Оптимальным решением станет обращение за помощью к квалифицированному педагогу, который поможет выявить причину сложностей и помочь с вычислениями. Например, найти в Запорожье курсы ментальной арифметики, благодаря которым цифры перестанут быть для детей чем-то пугающим, а большинство операций будут проводиться в уме. Такая подготовка позволит легко работать с дробями, выполняя сложение/вычитание, умножение/деление.
Деление дробей
Для деления обыкновенных дробей используется метод перекрестных действий:
числитель первого числа умножаем на знаменатель другого — результат станет числителем частного;
знаменатель второго числа умножаем на числитель первого — результат становится знаменателем частного.
Сложность в том, что для деления используется умножение — это как раз обычно и смущает школьников. Поэтому правило нужно просто заучить, повторив его многократно и отработав на многочисленных примерах. Только в этом случае дети запоминают, что когда речь идет о дробях, для деления используется умножение (перемножаем расположенные по диагонали числа, а результат записываем в числитель/знаменатель частного).
Важные нюансы
В изучении арифметических действий очень важна последовательность. Нельзя учить малыша читать, пока он не выучил все буквы алфавита — путаница и постоянные ошибки не только будут мешать, но и могут раз и навсегда отбить охоту к чтению. С математикой аналогичная ситуация:
нужно уметь правильно разделять большое число на несколько отдельных составляющих, с которыми проще провести требуемые операции;
сложение и вычитание должны быть отработаны до автоматизма;
к делению приступают только после тщательного изучения таблицы умножения.
Важно обратить внимание, что в качестве делимого выступает самое большое число — это поможет не запутаться при решении задач. А на ноль делить нельзя — подобный вопрос с подвохом часто встречается в заданиях, поэтому нужно не упустить этот момент.
Вывод
К каждому ребенку нужен свой подход — не существует единой методики, которая подойдет любому ученику. Кому-то проще оперировать цифрами, а примеры с яблоками или конфетами вызывают недоумение. Другие школьники по привычке считают на пальцах или на линейке — для них в качестве примера отлично подойдут задачи с покупками. Как объяснить ребенку деление? Начать с азов, пробовать разные методики, а если не удается достичь желаемого результата, довериться специалистам, обратиться к учителю или записаться на специализированные курсы, которые будут актуальны для детей в возрасте от 5 до 12 лет (подготовку к школе стоит начинать заблаговременно).
Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
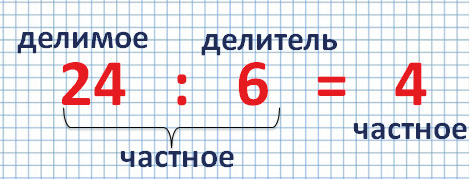
Числа при делении
При делении, как и при другом математическом действии, каждое число имеет свое название.
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Деление на 1
Деление на 0
Деление числа само на себя
Связь деления и умножения
Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях: