Как объяснить ребенку что такое миллиметр
Миллиметр
Знакомимся с новой единицей длины и продолжаем учиться выполнять измерения.
Ты уже знаком с такими единицами длины как дециметр и сантиметр.
Более мелкая единица длины — это миллиметр.
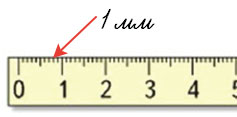
Как найти на линейке 1 мм?
Пишем «мм», а читаем «миллиметр».
Именованное число
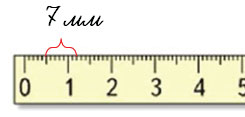
Как прочитать запись 7 мм?
Семь миллиметров.
«7» показывает, что единица измерения ММ содержится в данном числе 7 раз.
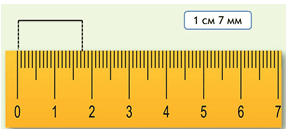
Производим измерения
Преобразования именованных чисел
Необходимо перевести в мм:
88 мм нужно представить в сантиметрах и миллиметрах. В числе 88 мм содержится полных 8 сантиметров.
Переводим миллиметры в сантиметры и наоборот
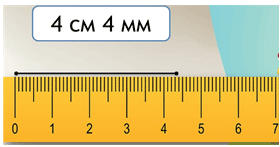
4 см 5 мм = 40 мм + 5 мм = 45 мм
63 мм = 60 мм + 3 мм = 6 см 3 мм
Сравниваем миллиметры и сантиметры
Сравнение именованных чисел
Именованные числа можно сравнивать.
Попробуем сравнить 2 см 3 мм и 23 мм. Удобнее сравнивать одинаковые единицы измерения, поэтому переведем в миллиметры величину 2 см 3 мм.
Сравнивая 23 мм с 23 мм, можем утверждать, что эти величины равные, значит,
Чертим отрезки
Поделись с друзьями в социальных сетях:
Занятие «Знакомство с единицей длины – миллиметр»
I. Организационный момент
— Только что пришёл сигнал из космоса. Дружественные нам инопланетяне давно наблюдали за вами, и захотели познакомиться с вами поближе и посмотреть, как вы живёте, они просят разрешения прилететь к нам в гости. Пригласим их?
— Но у них не точные данные о нашей планете. Надо помочь им успешно долететь до нашей планеты и найти нашу школу. Они будут присылать нам сигналы, а мы поможем им.
II. Повторение изученного материала
а) работа с геометрическим материалом
— У нас потерян кусочек карты вашей Галактики. Помогите нам восстановить ее.
— Давайте посмотрим, что случилось Вам необходимо определить, какой именно кусочек потерян.
Можете обсудить ответ в парах.
— Какая геометрическая фигура получилась?
— Определите периметр и площадь прямоугольника самостоятельно.
— Давайте перед выполнением задания вспомним, как связаны эти единицы измерения.
+ Чтобы найти площадь нужно длину умножить на ширину.
Самостоятельная запись решения детьми.
— В каких единицах длины мы получили площадь?
— выразите результат в кв. дм.
— Что мы должны знать?
7200 см 2 = 72 см 2
Проверьте себя в парах.
III. Сообщение темы.
— Какую самую маленькую единицу длины мы знаем?
IV. Знакомство с новым материалом.
— У нас на карте отмечены планеты, которые обозначены точками B, C, D. Помогите нам вычислить какая из них ваша планета и найдите точное расстояние до нее.
— Открываем учебник на стр.16 № 290. Здесь тоже есть эта карта. Читаем задание.
+ Расстояние от точки А до других точек.
+ АС = 4см и еще 3 деления, мерки.
АВ = 8см и еще 7 делений, мерок.
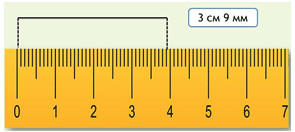
АD = 5см и еще 9 делений, мерок или 6см.
— К нам поступил следующий запрос.
— Мы знаем, что на карте ваша планета находится на расстоянии меньше 8 см, но больше 5 см.
— Какой отрезок подходит к этому условию?
При измерении этого отрезка кто-то назвал длину 5см, кто-то 6см. Но ведь одно маленькое деление на карте может означать миллионы километров в космосе. И наши друзья ошибутся в дороге. Теперь, я думаю, пришло время обратиться за помощью к нашим друзьям в учебнике Мише и Маше. Стр.17. Читаем.
Как называется одно маленькое деление на линейке?
Как теперь назовем длину отрезка АD?
+ Длина отрезка АD = 5см 9 мм
Переведем длину этого отрезка в миллиметры.
+ 5см = 50 мм, 50 мм + 5 мм = 59 мм.
— Вот мы и указали точное расстояние.
Какие единицы длины мы теперь знаем?
Осознание и осмысление учебной информации.
— Зачем нужны миллиметры?
+ Измерять маленькие предметы, для точности.
— Определите, в каких единицах длины удобнее измерять ширину стола? А толщину оконного стекла?
№ 291 (расположите единицы длины в порядке возрастания)
V. Закрепление изученного о величинах.
— Пока инопланетный корабль летит, мы с вами потренируемся в переводе известных нам величин. Стр.17 № 291
| а) устно по цепочке | б) в тетради самостоятельно |
| 1 км = :м | 4 км 128 м = :м |
| 1м = : дм | 14м 3 дм = : дм |
| 1 дм = : см | 6м 30 см = : дм |
| 1см = :мм | 43дм 8 см = :см |
| 1м = :см | 3 м 5 см = : см |
| 1м = :мм | 4 км 8 м = : м |
| 1км = :дм | 94 м 6 дм = :дм |
При проверке 2 ученика вписывают ответы на доске.
— А сейчас мы сделаем инопланетную зарядку
б) определение единиц для измерения
— К нам поступил следующий сигнал
.В нашем бортовом компьютере произошел сбой и он перестал показывать единицы измерения. Помогите нам! Заполните пропуски.
— стр.19 № 295. Какие же единицы измерения пропали?
(Устно с объяснением выбора единицы измерения).
а) расстояние между городами 760 :
б) высота полета самолета 12300:
в) площадь участка 420 :
з) длина карандаша 170 :
и) рост человека 160 :
к) длина комнаты 60 :
— Молодцы, помогли восстановить данные в компьютере инопланетян.
Чтобы починить наш компьютер, нужно три провода:
Хватит ли нам катушки с проводом длинной 2 м?
— Поможем рассчитать инопланетянам.
Что нужно сначала сделать, чтобы было удобно решить задачу?
+ Перевести в одни единицы длины.
Запишите краткое условие и решите задачу самостоятельно.
500 + 780 + 285 = 1565 мм
Ответ: катушки с проводом длиной 2 м хватит, чтобы починить компьютер.
— Ура! Мы починили корабль. Спасибо.
— Помогите им приземлиться. Космические гости не должны задеть елочку. Измерьте высоту елочек и найдите, какая меньше.
— С какой новой единицей длины познакомились?
— Чему учились на уроке?
VII. Домашнее задание.
ТПО № 2 (дополнить миллиметры до 1 см), № 4 (сравнить, переводя в одни единицы длины)
Как объяснить ребенку что такое миллиметр
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
Сантиметр, миллиметр, дециметр, метр. Что общего в этих словах? В каких случаях употребляются данные величины? Как соотносятся друг с другом?
Рассмотрим обычную школьную линейку.
Каждый сантиметр линейки разделён на 10 одинаковых частей. Одно такое маленькое деление называется миллиметром. В 1 см 10 мм. Миллиметры сокращенно записываются так: мм.
Так как в 1 см 10 мм, то в 2 см 20 мм, в 8 см 80 мм, в 14 см 140 мм. Соответственно, 60 мм – это 6 см, 130 мм – это 13 см. 37 мм = 3 см 7 мм, 6 см 2 мм = 62 мм.
Начертим отрезок длиной 10 см.
Выразим сантиметры в миллиметрах.
10 см – это 1 дм, значит, в 1 дм 100 мм.
Следовательно, в 7 дм 700 мм, 10 дм 1000 мм, 500 мм составляют 5 дм, 900 мм = 9 дм.
Если в 1 см 10 мм, то в 100 см 1000 мм.
Значит, в 1 м 1000 мм. Следовательно, в 3 м 3000 мм, в 8 м 8000 мм, а 5000 мм = 5м.
Сантиметр, миллиметр, дециметр, метр – всё это единицы длины. Но основной единицей длины в метрической системе является метр. Сантиметр, миллиметр, дециметр – дольные единицы метра.
В этих словах есть общая, одинаковая часть – «метр», происходящая от греческого слова, которое переводится как мера. Приставка «санти» происходит от латинского слова, означающего сто: 100 см = 1 м. Приставка «милли» также происходит от латинского слова, которое переводится как тысяча: 1000 мм = 1 м. А приставка «деци» означает десятую: 10 дм = 1 м.
10 мм = 1 см, 10 см = 1 дм, 10 дм = 1 м, 100 мм = 1 дм, 1000 мм = 1 м.
Конспект урока по математике на тему «Миллиметр» (2 класс)
Тема урока : Миллиметр.
Цель урока: Формирование представления о единице измерения длины – миллиметр.
— повторить изученное о единицах измерения длины – сантиметре и дециметре;
— познакомить с единицей измерения длины – миллиметром;
— показать соотношение между миллиметром и сантиметром;
— совершенствовать умение преобразовывать одни единицы измерения в другие;
— продолжать формировать умение сравнивать именованные числа,
— совершенствовать вычислительные навыки и умения решать простые задачи;
— научитесь измерять предметы и чертить отрезки, используя новую единицу измерения длины.
— развивать умение работать с линейкой;
— развивать познавательную активность, внимание, мышление;
— Воспитывать аккуратность работы в тетради.
— Воспитывать интерес к предмету через наглядность и современные виды заданий
Предметные: знают единицы измерения длины – миллиметр, сантиметр, дециметр ; умеют преобразовывать величины, сравнивать числа и именованные числа, решать задачи и выражения изученных видов.
Метапредметные (критерии сформированности/оценки компонентов УУД): познавательные: способны понимать учебную задачу урока, выделять и формулировать познавательные цели, строить логическую цепочку рассуждений, устанавливать причинно-следственные связи, работать с учебником; регулятивные: могут контролировать и оценивать собственную деятельность и деятельность партнеров, корректировать свою деятельность; коммуникативные: умеют достаточно полно и четко выражать свои мысли, слушать собеседника и вести диалог.
Личностные: имеют мотивацию к учебной деятельности; принимают и осваивают социальную роль обучающегося, овладевают начальными навыками адаптации в обществе; используют приобретенные навыки учебного сотрудничества со взрослыми и сверстниками в разных ситуациях; знают, как важны в учебной деятельности мышление, внимание, наблюдательность, аккуратность, личная ответственность
Материально – техническое обеспечение: учебник, проектор.
Осуществляемая деятельность учащихся
Формируемые умения (универсальные учебные действия
Приветствует учащихся, эмоционально настраивает на урок. Проверяет готовность класса.
— Прозвенел звонок веселый.
Мы начать урок готовы.
Будем слушать, рассуждать,
И друг другу помогать.
— Можете тихо сесть. Раз, два, три.
— Посмотрите, ребята, на своё рабочее место. Всё ли у вас готово к нашему уроку: учебник, тетрадь, ручка, простой карандаш и линейка.
Приветствуют учителя, эмоционально настраиваются на урок. Организуют свое рабочее место, проверяют наличие индивидуальных учебных принадлежностей на столе.
Регулятивные: умеют организовывать своё рабочее место.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
2. Актуализация опорных знаний
— Начнём наш урок с устного счёта. Не забываем поднимать руку. Внимание на доску.
— В каком числе цифра 7 обозначает единицы?
— В каком числе отсутствует разряд единиц?
— В каком числе цифра 9 обозначает десятки?
— В каком числе 8 десятков и 6 единиц?
— В каком числе 3 десятка и 4 единицы?
— Сколько в числе 25 десятков и единиц?
— Сколько в числе 13 десятков и единиц?
— Назовите однозначные числа.
— Назовите двузначные числа.
— Назовите числа в порядке убывания.
— А сейчас поиграем в игру «Домики». У каждой пары на парте лежат листочки с заданием. Вам необходимо сообща, быстро и правильно заселить домики, вписать в окошечки пропущенные числа. Та пара, которая справится с заданием, поднимает руки. Кому задание не понятно? Если всем понятно, приступайте к заданию.
— Сравните свои ответы с ключом на слайде.
— Поднимите руки та пара, у которой всё правильно.
— Поднимите руки та пара, у которой были ошибки.
— Как вы считаете, почему в вашей паре были ошибки?
— Откройте тетради, положите тетрадь под наклоном, запишите число, классная работа. Кто записал, положите ручки на край парты.
-С помощью какого знака можно записать арифметическое действие «сложение»?
-Это арифметическое действие можно записать с помощью знака «плюс» (прописываю образец на доске + + +).
-Запишите знак «плюс» в ваших тетрадях.
-Теперь послушайте ещё одно стихотворение-загадку:
Весит вместе с кошкой дама
Сорок девять килограммов,
А с собачкой та же дама
Весит сорок килограммов.
За неё реши задачку –
-Как записать этот знак? (прописываю на доске: > > >).
Слушают учителя; считают устно, выполняя арифметические действия сложения и вычитания, анализируют, сравнивают, доказывают; в ходе логических рассуждений делают выводы
Регулятивные: осуществляют контроль и корректировку своей деятельности и деятельности партнеров.
Предметные: владеют математическими терминами: уменьшить, увеличить, прибавить, вычесть; знают таблицу сложения в пределах 20, как получить последующее и предыдущее число.
Коммуникативные: умеют слушать и слышать; обосновывать свою точку зрения, доносить её до всех участников процесса
3. Подготовка к восприятию учебного материала
Создаёт ситуацию для определения темы, цели урока.
— Ребята, у каждого из вас на парте лежат карточки. Положите их перед собой. Что вы на них видите?
— Каким измерительным прибором мы можем измерить длину отрезков?
— Измерьте длину первого и второго отрезков.
— Чему равна длина 1 отрезка?
— Какими единицами измерения длины вы пользовались?
— Измерьте длину третьего отрезка. В чём сложность при измерении длины третьего отрезка?
— Как вы думаете, существует ли такая единица измерения длины, которая меньше сантиметра?
Может кто-то знает, как она называется?
— Она называется – миллиметр.
— Сформулируйте тему сегодняшнего урока.
— Верно, тема нашего урока «Миллиметр».
— Как вы думаете, какая цель сегодняшнего урока?
— Сегодня вы познакомитесь с новой единицей измерения длины «миллиметром». Узнаете, сколько раз 1 мм помещается в одном сантиметре. Научитесь измерять предметы, используя новую единицу измерения длины.
Измеряют длины различных предметов при помощи линейки, отвечают на вопросы учителя, рассуждают.
— Мы не умеем измерять длину таких маленьких отрезков, мы не знаем такую единицу измерения
— Мы думаем что существует
— Познакомиться с новой единицей измерения дины – миллиметр.
Регулятивные: контролируют и оценивают собственную деятельность и деятельность партнеров по образовательному процессу. Познавательные: осознанно и произвольно строят речевое высказывание в устной форме; структурируют знания.
Предметные: знают единицы измерения длины – сантиметр, дециметр; что в 1 дециметре содержится 10 сантиметров; умеют измерять предметы с помощью линейки.
Коммуникативные: вступают в речевое общение со всеми участниками образовательного процесса. Личностные: имеют мотивацию к учебной деятельности; осваивают социальную роль обучающегося
5. Открытие новых знаний
— Положите линейки перед собой и скажите, что на линейке вам знакомо? (дм и см)
— Что на линейке вам неизвестно, но вы хотели бы узнать? Обратите внимание на деления м/у см, видите маленькие чёрточки.
-Оказывается, это тоже единицы измерения длины. Они называются…. (миллиметры)
– Расстояние от одного такого деления до другого составляет 1 миллиметр. Покажите друг другу в парах 1 мм.
— Значит, как называется единица измерения длины, которая меньше сантиметра?
– Посчитайте, сколько таких делений (миллиметров) содержится в одном сантиметре.
— Значит, чему равен 1 см?
— Давайте запишем это в тетради. Но слово миллиметр очень длинное, и математики-учёные, договорились обозначать эту запись кратко, двумя буквами. Догадайтесь, какими, если
«Сантиметр» обозначается см
Как же мы обозначим «миллиметр»? (мм)
Сделаем запись в тетрадь
Слушают учителя, выполняют необходимые действия; рассуждают, измеряют длины отрезков, чертят отрезки заданной длины; переводят сантиметры в миллиметры и наоборот; осуществляют взаимо- проверку
— В 1 сантиметре содержится 10 миллиметров
Регулятивные: формулируют учебную задачу; осознают, что уже усвоено и что предстоит узнать и усвоить; контролируют и оценивают свою деятельность и деятельность партнеров по образовательному процессу. Познавательные: анализируют, сравнивают, логически рассуждают, делают выводы. Предметные: знают единицу измерения длины – миллиметр; знают, что 10 миллиметров составляют 1 сантиметр; умеют преобразовывать единицы измерения длины как большую в меньшую, так и наоборот, правильно измеряют отрезки и чертят отрезки заданной длины. Коммуникативные: умеют слушать, слышать и понимать партнера, управлять поведением партнера, приходить к общему мнению. Личностные: имеют мотивацию к учебной деятельности; осваивают социальную роль обучающегося.
Регулятивные: контролируют свои действия, соотнося их с действиями учителя и одноклассников. Личностные: имеют мотивацию к учебной деятельности, развиваются навыки сотрудничества
Нам пора передохнуть,
Потянуться и вздохнуть.
Покрутили головой, –
И усталость вся долой!
Раз-два-три-четыре-пять,
Шею надо разминать.
Встали ровно. Наклонились.
Раз – вперед, а два – назад.
Потянулись. Распрямились.
Повторяем все подряд.
А потом мы приседаем.
Это важно, сами знаем.
Мы колени разминаем,
Наши ноги упражняем.
А теперь на место сели,
Принимаемся за дело
Выполняют элементарные физические упражнения (в соответствии с текстом стихотворения), повторяя их за учителем: потягивания, вдох и выдох, вращения головой, наклоны вперед и назад, приседания, ходьба на месте
7. Осознание и осмысление учебной информации
— Ребята, как вы думаете, зачем нужны миллиметры?
— Не зная миллиметров вы, например, могли бы мне точно сказать толщину вашего учебника по математике?
— А теперь можете? Измерьте и скажите.
— Определите, в каких единицах длины удобнее измерять ширину стола? А толщину оконного стекла?
Измеряют толщину учебника, отвечают на вопросы
— измерять маленькие предметы, измерять предметы для точности.
Регулятивные: контролируют и корректируют собственную деятельность, выделяют и осознают, что уже усвоено и что предстоит усвоить. Познавательные: строят логическую цепочку рассуждений, анализируют, сравнивают, делают выводы; аргументируют выбор знака действия
8.Первичное закрепление учебного материала.
— Знаете ли вы название самой маленькой птицы?
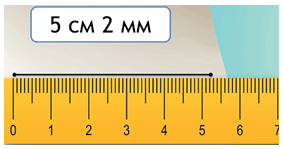
— Самая маленькая птица– колибри, птичка, уступающая размерами многим насекомым. Ее длина всего 5 см 7 мм. Начертите в тетрадях такой отрезок.
— Комары – летающие насекомые небольшого размера (длиной 4 – 14 мм) Начертите отрезок равный 14 мм.
а) работа с учебником
-А сейчас поработаем в учебнике. Откройте учебники на странице 10, выполним задание 2.
-Как называются линии, изображённые в задании?
-Измерьте длину данных отрезков.
-Чему равна длина голубого отрезка?
-Сколько это составляет миллиметров?
-Какова длина розового отрезка?
-Выразите её в миллиметрах?
-Молодцы. Выполните задание в парах. Начертите отрезок длиной 30 миллиметров.
-Проверьте работу друг друга и выразите длину данного отрезка в сантиметрах (3 см).
В)Выполним задание 3. Вы должны сравнить числа и поставить знаки =, >,
-Теперь сравните 10 мм и 9 мм. Что больше?
2) 20 мм … 2 см.
-Объясняй, как ты будешь выполнять
3) 1 см 8 мм … 18 мм.
-Выполним задание 5. Вам нужно выполнить действия (у доски, по цепочке).
— Прочитайте задачу под №4 и представьте жизненную ситуацию.
— Прочитайте задачу вслух.
— Что значит число 7
— Что значит число 20
— Какой вопрос задачи, что нужно узнать?
— Запишем краткую запись.
— Сколько дм была высота ёлочки весной?
— На сколько см она выросла за лето?
— Каким действием следует решать задачу?
— Можем ли мы сразу выполнить вычисления?
— Выполните соответствующее преобразование чисел и решите задачу.
Чертят отрезки в тетрадях, работают по учебнику
Методики репетитора по математике. Работа с темой «единицы измерения» в 5-6 классах
М аленькому ученику 5-6 класса часто с трудом даются переводы величин из одной единицы измерения в другую. Это касается всех тем: длин, площадей, единиц массы и объемов. Если вы репетитор по математике, то наверняка встречались с подобной проблемой. Почему она возникает? На мой взгляд причин несколько:
1) Возраст и уровень развития 5 классника еще не дает ему возможность мыслить абстрактно, и для того, чтобы как-то решать предложенные репетитором по математике задачи ему приходится запоминать большое количество информации о способах перевода. Заучивать или осознавать комбинации разных действий с разными соотношениями и с разными направлениями перевода. Часто такую операцию приходится выполнять с объектами, не представленными перед детьми в их реальном виде, которые воспринимаются как наборы букв, а не как отрезки, квадраты или кубы. Естественно, что в такой слабой модели реальных величин как их буквенная запись, детям очень трудно находить объяснения своим действиям. Обойтись без них на практике они тоже не могут, так как не видят единого и четкого правила для переводов. Конечно, из метров в сантиметры — один способ перевода, а из миллиметров в сантиметры уже другой. Трудно каждый раз пытаться представлять себе данную величину в реальных размерах.
2) Некоторые репетиторы по математике и школьные учителя, занимающиеся индивидуально считают, что важно донести логику переводов, описывая каждый из них словами. В результате слабому ученику приходится еще тратить ресурсы мышления на анализ этих текстов.
3) Ребенок почти всегда не имеет возможности обратиться к реальному объекту и проверить то, что именно он в нем считает. Приходится работать в некотором роде вслепую, потому как репетитору по математике очень непросто обеспечить визуальное сопровождение к выполняемым операциям. Аккуратно показать на рисунке, например, что в одном гектаре ровно 100 ар можно только моделируя эти квадраты в масштабе, условно договариваясь о размерах отрезков, отвечающих за длины их сторон. Я уже не говорю о том, что нужно представлять себе площадь, например, в 4 га, 5 га. Тетрадный лист удобен только для показа соотношения между 1 дм и 1 см. В таких условиях опорой репетитора может стать — соответствующий для понимания уровень абстрактного мышления ребенка, способного оперировать отвлеченными от картинки образами переводимых величин. Но что делать, если его нет?
Как объясняют эту тему среднестатистический репетитор по математике и школьный преподаватель? Один ар — это квадрат размером 10×10 м, а один гектар — это квадрат размером 100×100 м. Так как в одном гектаре получается 100 

Задумайтесь, поможет ли ему тот же саамы стандартный текст учебника, но только в исполнении репетитора математики? Запомнит ли он, какое именно арифметическое действие совершить в том или ином случае для разных направлений перевода? И почему именно их? Как работать с площадью 15га (или с 15,2 га в 6-ом классе), если ее надо во что-то перевести? В лучшем случае от объяснений репетитора в памяти останется равенства 1га=100а.
В обучении важную роль играет деятельный метод познания. Ребенок получает навыки и представления об объектах в ходе практической работы с ними. Запоминание — ключевой фактор не только для получения возможности выполнить преобразование правильно, но и для понимания особенностей и взаимосвязей между используемыми понятиями. Для того чтобы лучше понять и запомнить материал, ребенку нужно самостоятельно с ним поработать (в случае с величинами — выполнить достаточное количество переводов). А для того чтобы правильно работать нужно понимать материал. Понимать, что ты делаешь. Получается замкнутый круг, который репетитору по математике бывает очень сложно разорвать.
Одним из способов это сделать — создать иллюзию понимания процесса на паре простых примеров и сразу же с ее помощью объяснить какой-то простой алгоритм решения всех подобных задач, закрепляя его соответствующей системой упражнений. В качестве такого подхода к теме «единицы измерения» я бы предложил метод четкой систематизации и четких единых правил перевода в другую единицу измерения. В учебниках, к сожалению эти правила не изложены в виде готового алгоритма, а предполагается, что ребенок со временем сам его построит. Но родители требуют от репетитора по математике решить проблему именно сейчас, а не надеяться на далекое будущее.
Советую репетиторам по математике объяснить сначала ученику метод перевода, например, 3-х сантиметров в миллиметры через обычную линейку. После просьбы посчитать количество маленьких делений, тут же попросить подобрать действие. по которому можно было бы из числа 3 получить число 30. Ответ часто дают даже слабые дети: надо умножить 3 на 10. После этого обратить внимание на то, что мы перевели КРУПНУЮ единицу измерения в МЕЛКУЮ, а число для перевода взято такое, которое показывает сколько в 1 сантиметре миллиметров. Сразу же стоит обсудить перевод из миллиметров обратно сантиметры и заметить, что мы переводим МЕЛКУЮ единицу в КРУПНУЮ и при этом ДЕЛИМ на это же число, то есть на 10. Репетитору по математике нужно сказать ребенку, что способ перевода делением и умножением работает всегда и со всеми величинами: длинами, площадями, объемами и единицами массы и времени. Важно только найти переводящее число. Это число показывает количество сколько мелких единиц из которых состоит крупная.
Для быстрого и удобного поиска переводящих чисел, а также для того, чтобы быстрее заучить основные соотношения, лучше всего выстроить единицы длины по порядку от мм до км и составить такую схему:
Между каждыми соседними единицами измерения стоит переводящее число, на которое в случае перевода в меньшую единицу измерения надо умножить, а в случае перевода в более крупную (правую) поделить. Если для перевода даны не соседние единицы, а расположенные через одну — надо выполнить два перехода. Через три — три перехода. В этом случае переводящее число будет составлено путем совмещения единицы и всех нулей, которые мы встречаем по дороге. При движении вправо (то есть при переводе в БОЛЕЕ КРУПНУЮ единицу) мы делим, а при движении влево (то есть при переводе в МЕЛКУЮ) — умножаем.
В какой-нибудь удобный момент своих объяснений репетитор по математике должен обязательно обратить внимание ученика на тот факт, что для покрытия фигуры более мелкими единицами измерения площади потребуется большее их количество. Этот простое наблюдение поможет ребенку укрепить уверенность в том, что действие по переводу в меньшую единицу измерения выбрано правильно и надо не делить, а умножать на переводящее число (так как при умножении, говоря языком школьника, «становится больше»). На практике объяснения репетитора по математике даются более точно и просто: находи дорогу по стрелкам к нужной величине и делай те действия, которые «по дороге» встречаются.
Репетитору желательно выделять определенные закономерности поведения разрядов чисел, которые ребенок вряд ли сам заметит или не сможет формулировать по ним четкие правила перевода: сколько нулей стоит над стрелками — столько правых знаков надо удалить при переводе (отделить запятой для 6-классника) или столько нулей справа надо добавить (в зависимости от направления перевода). Или еще короче: идем вправо — убираем столько знаков сколько видим нулей. Движемся влево — добавляем нули.
Изучив все детали процесса перевода длин, репетитор по математике переходит к площадям. Аналогия полная. Главное расположить единицы измерения площадей в порядке их увеличения и записать в теоретическую тетрадь следующую схему:
То же самое для объемов. Схема приведена ниже. При таком едином подходе у ребенка не возникнет путаницы, что ему делать в каждом конкретном примере, а поскольку вся практическая работа ученика строится на этих схемах, то они постоянно будут находиться перед его глазами. В какой-то момент выполнения упражнений репетитор по математике может попросить закрыть теоретическую тетрадь и выписать на листочке или в рабочую тетрадь эту схему. Такое же задание можно предложить в качестве упражнения на дом. Например, перед каждым номером, даже перед каждым переводом, сначала переписать (или по памяти выписать) величины в порядке их роста. Работа зрительной памяти вместе с моторной сделают свое дело и через какое-то время ребенок сможет выполнять подбор переводящего числа в уме, удерживая перед глазами эту таблицу как знакомую фотографию.
Схема для единиц объемов:
Представление о расположении величин порядку их размеров в реальности постепенно складывается при заучивании всего ряда. Ребенок будут понимать, что если единица измерения расположена справа, то она крупнее той, что слева, и чем правее, тем крупнее.
Репетитору по математике важно не растерять с учеником навыки работы с этими схемами. Обязательным пунктом методики работы репетитора является обращение к ней в течение всего цикла занятий с учеником. Необходимость частого использования схем в старших классах постепенно снижается по мере того, как ребенок запоминает соотношения. Для этого нужен не один год. Чем выше становится со временем уровень его развития, чем чаще он сталкивается с величинами в жизни (не обязательно с математическими), тем проще и быстрее он выполняет переводы. И тем реже можно проводится повторение.
Колпаков Александр Николаевич, репетитор по математике Москва. Профессиональный репетитор в Строгино.