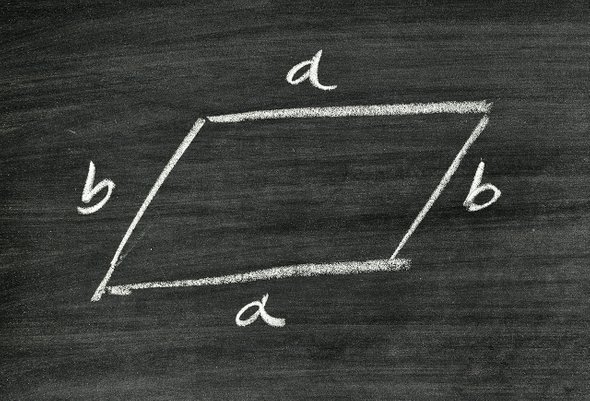Как объяснить ребенку что такое площадь и периметр

Сценарий урока на тему Различение площади и периметра.

Урок по различению понятий площади и периметра.

Цель: ученик, умеющий различать понятия площадь и периметр

учить различению понятий площадь и периметр через построение идеального образа

продолжить совершенствование математической речи обучающихся и умения выступать с самостоятельными суждениями и отстаивать их.

способствовать развитию умения работать в группе

содействовать воспитанию познавательного интереса к предмету

Ребята, давайте поздороваемся с гостями.

Ваши знания зависят только от вас. И целью нашего урока является различение основных понятий «Периметр. Площадь.» и применение ваших знаний на практике.

2. Этап предварительной диагностики (актуализация знаний)

1. Повторение изученного по теме «Периметр. Площадь.»

Посмотрите на экран.

— Что вы видите на слайде?

— По каким признакам мы можем разбить эти фигуры на группы?

— Найдите лишнюю фигуру и подберите основание.

— А теперь посмотрим на четырёхугольник.

— Что мы можем измерить у четырёхугольника?

— Каким инструментом нужно пользоваться?

— Что ещё можем найти у четырёхугольника?

— Что такое периметр?

— Знаешь ли ты в каких единицах измеряется периметр?

Вот мы с вами повторили все те знания, которые помогут нам сегодня на уроке.

Рисуй глазами треугольник

Рисуй глазами треугольник.

Теперь его переверни

ты по периметру веди.

Рисуй восьмерку вертикально.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы, наконец.

— лишний четырёхугольники

Источник

Периметр и площадь. Почему дети в начальной школе путаются в том, что кажется взрослым очень простым

Нам, взрослым, некоторые вещи кажутся очевидными. Всем мы знаем, как вычислить периметр и площадь у фигуры, например. А вот для детей в началке это сложно. Как им помочь, рассказывает наш блогер, учитель начальных классов Ольга Катаева.

Родители по-разному относятся к вопросу выполнения домашнего задания. Некоторые помогают, корректируют, контролируют. Некоторые делают задания за ребёнка. А кто-то считает, что выполнение домашнего задания — ответственность ребёнка, и не вмешиваются.

Есть родители, которые предпочитают с детьми не заниматься совсем (это касается не только домашних заданий). Восхищают родители, которые занимаются со своими детьми, помогают им понять то, что решали в классе, разбирают ошибки в контрольных. А есть такие, которые не разбирают материал вместе с ребёнком, а требуют полного заучивания программы, не интересуясь, понял он что-то или нет.

Много раз объясняла родителям, что у детей начальных классов другое мышление

Они не могут думать абстрактными понятиями. Они не могут понять материал, заучив правило или формулу. Чтобы научиться говорить определениями и формулами, младшие школьники должны усвоить понятие на практике.

В начальной школе есть совсем простые темы, а есть темы потруднее. Есть очень трудные. Одна из них — «Площадь и периметр». Взрослым, у которых логическое мышление уже сформировано, эта тема не кажется трудной, поэтому они с лёгкостью объясняют её дома детям, не придерживаясь рекомендаций и объяснений учителя. Родители помнят, как учили эту тему в школе. Правда, не в начальных классах, а в среднем звене и старшем — то есть тогда, когда начинает формироваться логическое и абстрактное мышление. Поэтому подросткам дают формулы.

Дети начальной школы часто путают понятия «площадь» и «периметр»

Объяснению и повторению этой темы уделяется не так уж много времени. Родители, видя двойки за контрольные с такими заданиями, пытаются по своему объяснить, как решать. Дают формулу на периметр: P=2а+2b, но не объясняют, что она обозначает.

Вспомним формулу площади S=ab. И в той, и в другой формулах присутствует умножение — это первая причина, почему дети путаются (другие причины надо выяснять, это могут быть пространственно-конструктивные нарушения и др.).

Как можно объяснить эту тему, чтобы ребёнок ее понял? Обратимся к определению периметра: «Пери́метр — общая длина границы фигуры», или «Периметр — длина контура замкнутой плоской фигуры», или так: «Периметр — сумма длины всех сторон плоской геометрической фигуры». В начальной школе даётся такое определение: «Периметр — это сумма длин всех сторон фигуры». Важно понять, что периметр — это весь контур фигуры, то есть мы складываем вместе длины всех сторон.

Когда мы говорим о площади, мы говорим о «части плоскости, заключённой внутри замкнутой геометрической фигуры», о том, сколько места занимает фигура на плоскости. Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее). Если фигура — прямоугольник, её делят на равные квадратики и считают их. Так можно делать с небольшими фигурами, которые помещаются в тетрадках.

Находить площадь «Красной площади», которая в Москве, так нельзя

Есть формула. Для нахождения площади больших фигур, прямоугольной формы, достаточно знать длину и ширину и перемножить их (можно ввести ассоциацию с таблицей Пифагора, которая тоже поделена на квадратики и значение произведения находят путём умножения чисел).

Вот оно — существенное отличие: периметр — сложение, площадь — умножение. Поэтому в период, когда идёт отработка этих понятий, не следует вводить формулу периметра прямоугольника с умножением. Если ученик поймёт суть понятия «периметр», он сможет найти периметр любого многоугольника. Если зациклить его на формуле для нахождения периметра прямоугольника, школьник не сможет перенести знание для нахождения периметра другой фигуры.

Не надо заучивать с детьми формулы и определения. Надо понимать возрастные особенности младших школьников и объяснять на понятном для них «языке» — через образы, ассоциации, через практику, через действование.

Удачи родителям, которые понимают своих детей и помогают им в нелёгкой учебной жизни.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Источник

Живите сегодня!

персональный блог Лены Даниловой

Интересная математика. Учимся измерять площадь

Конечно же, тему «площадь» будут проходить в школе, как и многие другие темы. Но почему-то многое в школе или непонятно, или неинтересно, или и то, и другое.

Я знакомила своих детей с разными математическими темами задолго до школы. Но, конечно же, не на школьном уровне — а просто для формирования понятий.

Например, тема «Площадь» доступна примерно с 5 лет. Как только ребёнок может сосчитать кубики или квадратики, то он уже готов.

Можно начать с игр с кубиками.

Сложите из кубиков одинакового размера (из строительного набора, или из игры «Сложи узор», или игры «Уникуб») любую фигуру. Для начала попроще и поменьше. Предложите ребенку пальцем сосчитать все кубики, которые составляют фигуру. Скажите, что общее их количество называется площадью фигуры.

Сколько места занимает фигура в некоторых единицах измерения, так в числовом виде выражается ее площадь. А единица измерения здесь – квадратик – грань кубика.
Впрочем, показать проще, чем объяснить, даже если объяснять простыми словами. Поэтому сложите несколько фигур разной формы и площади и вместе с ребенком сосчитайте их площадь.

Предложите ребенку самостоятельно сосчитать площади других фигур, выстроенных из кубиков. Это не должны быть только квадраты и прямоугольники — фигуры могут быть очень разными!
Потом пусть ребёнок построит фигуры для вас, а вы считайте площадь.

Измеряем площадь плитками

Если у вас дома есть место, где пол выложен плиткой одинаковой формы (без вставок бордюров), предложите ребёнку измерить площадь комнаты (ванной комнаты, например) в плитках. То есть, сосчитать, сколько плиток занимает площадь пола. Если кроме целых плиток есть половинки или кусочки плиток, попробуйте складывать их (примерно, приблизительно!) в целые в уме и в итоге получить площадь с точностью до «столько-то плиток и еще такой-то кусочек» (половинка или меньше половинки, например).

Засаживаем полянку

Можно использовать конструктор «Лего», тогда площадь будем считать «пупырышками». И можно использовать детали из 2 пупырышков, четырех, восьми. Можно брать «однушки» — с одним пупырышком, или длинные детали, где пупырышки в один ряд.

Предложите ребёнку засадить разными «цветами» поляку для игровых человечков или других персонажей.
Полянка может быть любой формы. Но лучше начать с квадратной или прямоугольной. Посчитайте площадь.
Обратите внимание ребенка на то, что можно сосчитать не только площадь целиком, но и сколько рядов деталей или пупырышков и сколько их в каждом ряду. После этого говорите что-то вроде: «шесть рядов по три — получилось восемнадцать». Не надо требовать запоминания, достаточно, чтобы ребёнок слышал.

Площадь фигур на математическом планшете

Одно из моих любимых математических пособий — планшет с гвоздиками. На нём мы изучали очень много математических тем, в том числе — высчитывали площадь фигур.
Начинали с квадратов, прямоугольников. Потом я подбрасывала идею попробовать найти площадь треугольника. Немного помучившись, дети доходили до решения своим умом. И это было на уровне открытия! Не зная никаких правил, теорем, формул, дети догадываются, как на пальцах высчитать площадь треугольника, а потом и любой сложный многоугольник им по плечу!

Кроме вычисления площади уже готовых фигур, на планшете можно предложить детям рисовать резиночками фигуры заданной площади, но разной формы. И тут уж простор для творчества! Только не надо никуда спешить!

Квадратный сантиметр

Ваши дети уже знают, что такое сантиметр? А теперь узнают, что такое квадратный сантиметр.
Скажите ребёнку, что квадратик, у которого все стороны равны 1 см и называется квадратный сантиметр.
Нарежьте из миллимитровой бумаги 20 квадратных сантиметров и попробуйте заполнять им, например, поверхность спичечного коробка, ластика, небольшой коробочки.
Нарисуйте на лист обычной бумаги в клетку несколько фигур разной формы, разделенных на квадратные сантиметры. Предложите ребёнку сосчитать, сколько квадратных сантиметров составляет площадь каждой из фигур.

Квадратный метр

Изобразите на полу квадратный метр. Например, малярным скорчем или просто выложите метровыми лентами. Можно вырезать квадратный метр из куска широких обоев. Можно еще разбить его на квадратные дециметры. А один из них — на квадратные сантиметры или вообще — один из них заклеить кусочком миллиметровки, чтобы показать и квадратные сантиметры и квадратные миллиметры.

Попробуйте, сколько людей может встать на один квадратный метр. Сколько игрушек туда войдет? Сколько коробок от обуви (например, если у вас есть такие коробки) надо выложить, чтобы его заполнить и так далее.
Попробуйте измерять площадь комнаты в квадратных метрах (если у вас есть вырезанный из бумаги квадратный метр), сделайте вывод, что это неудобно. Но пока не говорите, как лучше сосчитать площадь.

Что дальше?

Вообще, в дошкольном возрасте этого достаточно. Хорошо, если в дальнейших играх вы так или иначе будете обращать внимание ребёнка на площадь фигуры. Рано или поздно это станет столь же естественным, как счёт.

Кстати, тема «Площадь» детям даётся даже проще, чем периметр. Потому что площадь можно увидеть наглядно, пощупать, ощутить, а периметр «пощупать» сложнее.

О периметре мы поговорим как-нибудь в другой раз.

Акция! До 1-го декабря скидка на набор презентаций по математике, записи прямых эфиров и на спецкурсы «Матемашка»!

Не забудьте подписаться на обновления блога:

Источник

Умение применять знания в нахождении периметра и площади геометрических фигур

2. Развивающая. Использовать на уроке развивающие упражнения, активизировать

мыслительную деятельность школьников.

3. Воспитательная. Обеспечить развитие ценностно-смысловой культуры учащихся;

совпадение ожидания и результата.

1. Организационный момент и сообщение темы урока.

Учитель: Здравствуйте, ребята. Сегодня мы продолжим изучение большой темы под названием “Площадь и периметр”. Тема нашего урока сегодня :“Умение применять знания в нахождении периметра и площади сложной фигуры”. Сложная фигура – это геометрическая фигура, состоящая из нескольких простейших фигур. Сначала, повторим то, что мы с вами изучили на прошлых уроках.

Задачи на развитие.

Учитель: Найдите площадь данной фигуры, если сторона квадрата 1 см.

Фигура изображена на доске.

Учитель: Правильно. Следующее задание. Уберите 3 палочки, чтобы осталось 3 таких квадрата.

Ученик выходит к доске и убирает 3 палочки.

Учитель: Уберите 4 палочки, чтобы осталось 3 таких же квадрата.

Ученик выходит к доске и убирает 4 палочки. Решение.

III. Работа по теме урока

Учитель: Какие геометрические фигуры вы уже знаете?

Учитель: Правильно. Что мы знаем о квадрате?

Ученик: У квадрата 4 стороны и 4 угла.

Учитель: Правильно. Каким свойством обладают стороны квадрата?

Учитель: Правильно. А какие углы у квадрата?

Учитель: С помощью чего мы можем построить прямой угол?

Ученик: С помощью треугольника.

Учитель: Давайте построим квадрат со стороной 4 см в вашей тетради. С помощью каких инструментов мы будем чертить квадрат?

Ученик: С помощью линейки, карандаша и треугольника.

Ученики в тетрадях строят квадрат и раскрашивают его.

Учитель: Эта геометрическая фигура. Как найти периметр и площадь этого квадрата?

Ученик: Периметр – это сумма всех его сторон. Сторон у квадрата 4. Значит, 4 сложим 4 раза.

Учитель: Как это записать?

Ученики делают запись в тетради: “Найти площадь фигуры F1”.

Ученика вызывают к доске, и он пишет: Р = 4 + 4 + 4 + 4 = 16 (см)

Ученики делают запись в тетради.

Учитель: В каких единицах еще измеряется периметр?

Ученик: В сантиметрах, в миллиметрах, в метрах, в дециметрах, в километрах.

Учитель: Молодец! Как еще можно записать периметр?

Ученик: С помощью умножения.

Ученик записывает на доске: Р = 4 · 4 = 16 (см)

Ученики записывают в тетради.

Учитель: А чему равна площадь квадрата?

Ученик: Длину квадрата умножаем на его ширину. Так как стороны у квадрата равны, то

Учитель: Какие еще единицы измерения площади вы знаете?

Ученик: квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный миллиметр.

Учитель: А теперь усложним задачу. Перед вами лежит карточка.

Ученики выполняют эту работу и делают запись в тетрадке: “Найти площадь фигуры F2”.

Ученик: Нужно найти площадь маленького квадратика со стороной 2 см.

Ученик выходит к доске и записывает – S2 = 2 · 2 = 4 (см 2 )

Ученики делают запись в тетрадке

Учитель: Правильно. А что можно сделать дальше? Мы вырезали этот квадратик и из большого квадратика, вынули его. Как найти площадь нашей фигуры?

Ученик: Из площади большого квадратика вычесть площадь маленького.

Ученик записывает на доске – S = S1 – S2 = 16 – 4 = 12 (см 2 )

Ученики делают запись в тетрадке.

Учитель: Внимательно посмотрите на эту фигурку и скажите, как еще можно измерить площадь? Можно ли эту фигуру как-то разрезать, чтобы получить фигуры, уже знакомые вам?

Ученики думают и говорят разные варианты.

Один из вариантов оказался очень интересным.

Учитель: Молодец! А что дальше?

Ученик: А дальше можно найти площади этих прямоугольников и сложить, потому, что наша фигурка тоже сложена из этих прямоугольников.

Ученики разрезают фигуру, как показано на доске.

Учитель: А как находится площадь прямоугольника?

Ученик: Нужно длину умножить на ширину.

Учитель: У вас получилось четыре фигуры. Что можно сказать про них?

Ученик: Две фигурки, как близнецы – одинаковые, и вторые две – тоже одинаковые.

Можно найти площадь одной фигуры и умножить на 2.

Ученик решает на доске: S1 = 1 · 4 = 4 (см 2 )

S = 2 · S1 + 2 · S2 = 2 · 4 + 2 · 2 = 8 + 4 = 12(см 2 )

Учитель: Молодец! У нас получилась то же значение площади, что и раньше.

Учитель: Вы, наверное, устали?

Настало время отдыхать.

Каждый день по утрам
Делаем зарядку (ходьба на месте).
Очень нравится нам делать по порядку:
Весело шагать (ходьба),
Руки поднимать (руки вверх),
Приседать и вставать (приседание 4-6 раз),
Прыгать и скакать (10 прыжков).

Учитель: А теперь сели за парты и

посмотрите на следующую модель. Фигура F3

Как найти площадь этой интересной фигуры?

Ученик: Треугольник, который выступает

можно отрезать и подставить в ту часть, где

треугольник “уходит” внутрь.

Учитель: Давайте возьмем ножницы, отрежем треугольник и подставим в верхнюю часть.

Что за фигура у нас получилась?

Учитель: Как найти площадь этого прямоугольника,

Если стороны нам неизвестны.

Ученик: Мы можем взять линейку и измерить

длину и ширину прямоугольника.

Ученики делают запись – “Найти площадь фигуры F3”.

Ученики линейкой измеряют длину и ширину. Получается длина, а = 6 см, ширина в = 2 см.

Ученик: Площадь данной фигуры равна S = 6 · 2 = 12 (см 2 ).

Учитель: Но это еще не все. Перед вами следующая фигура. Необходимо найти ее площадь.

Что за фигура перед вами?

Ученик: Треугольник. Но площадь треугольника

мы не умеем находить!

Учитель: Это правда. Из этого треугольника

сделаем прямоугольник. Я вам подскажу. Фигура F4

Сначала мы этот треугольник сложим пополам

Ученики: Мы поняли! Правую

Ученик: С помощью линейки измеряем

длину а и ширину в, и по S = а· в,

Учитель: Если мы при измерении, мы

будет выражена в мм, а ширина в см,

Ученик: Обязательно длину и ширину перевести в одну единицу измерения.

Ученики записывают в тетрадке: “Найти площадь фигуры F4”.

Учитель: А теперь я предлагаю поработать в паре. Вас за партой двое. Один ученик ( I вариант) находит периметр данной фигуры, а второй ( II вариант )- площадь.

Для этого начертим в тетради эту фигуру. После того, как вы выполните задание, поменяетесь тетрадями и проверите результаты друг у друга.

Ученики выполняют задание и результаты

записывают в тетрадь.

Учитель: Что у вас получилось?

Ученик: Квадрат со стороной 3 см. Р = 3 · 4 = 12(см)

S = 3 · 3 = 9 (см 2 ) 3 см

Учитель: Молодцы! А теперь я вам предлагаю поработать самостоятельно.

Найти площадь следующей фигуры. Она лежит перед вами.

VI. Самостоятельная работа по закреплению изученного материала.

Учитель раздает заранее заготовленные фигуры.

Ученики самостоятельно, без помощи учителя, разрезают эту фигуры, получают три прямоугольника.

Ученики делают запись: “ Найти площадь фигуры F5”.

Ученики находят S1 = 4 · 3 = 12(см 2 ), S2 = 2 · 1 = 2(см 2 ), потом находят площадь данной фигуры: S = S1 + S2 + S2 = 12 + 2 + 2 = 16 (см 2 ) и делают запись в тетради, затем

записывают: “Ответ: S = 16 см 2 ”.

Учитель: Понравился урок?

Учитель: Что вы нового узнали на этом уроке?

Ученик: Мы научились находить площадь и периметр сложных фигур. Это оказалось очень просто. Нужно немного подумать и эту фигуру перестроить или переделать в ту, периметр и площадь, которой, мы уже умеем находить.

Учитель: Я очень рада, что вам понравилось. Дома еще раз повторить формулы нахождения периметра и площади квадрата и прямоугольника; вспомнить, как переводить одну единицу

Учитель выставляет оценки.

VII. Домашнее задание: учебник стр. 77 № 8.

Источник

Как найти площадь и периметр?

Разделите периметр на 4: это дает вам длину одной стороны. Затем возведите эту длину в квадрат: это даст вам площадь. В этом примере 14 ÷ 4 = 3.5.

Соответственно, что такое периметр в математике?

Периметр общая длина границы любой замкнутой формы. … Если вам известна длина одной стороны фермы, вам просто нужно умножить ее на 4, чтобы найти общий периметр фермы.

далее, что такое пример периметра?

Таким образом, как решить вопрос о периметре? Решение: Если периметр квадрата равен 24 см, то его сторона будет 24 ÷ 4 = 6 см. Если периметр треугольника 15 см, а длина одной из его сторон 6 см, то общая длина двух других будет 15-6 = 9 см. Периметр красной фигуры 9 + 6 + 6 + 6 = 27 см.

Где используется периметр?

Мы часто находим периметр, когда установка рождественских огней вокруг дома или ограждение сада на заднем дворе. Другие примеры могут включать определение общей длины границы футбольного поля или длины вязания крючком или ленты, необходимой для покрытия границы коврика для стола.

Что такое периметр и площадь?

Почему важны площадь и периметр?

Как периметр применяется в нашей повседневной жизни?

Как объяснить ребенку периметр?

Как площадь и периметр работают вместе?

Площадь представляет собой пространство, занимаемое объектом., а периметр представляет собой границу фигуры. Измерение площади представляет собой два измерения и выражается в квадратных единицах, таких как квадратные километры, квадратные футы или квадратные дюймы.

Что такое формула площади?

Как вам район?

Чтобы найти площадь прямоугольника, умножьте его высоту на ширину. Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это на себя, чтобы найти площадь.

Почему мы учим учеников рассчитывать площадь и периметр?

Единица и темы по площади и периметру важны к математике, потому что это физические аспекты математики. Они являются основой для понимания других аспектов геометрии, таких как объемные и математические теоремы, которые помогают нам понять алгебру, тригонометрию и исчисление.

Что такое пример области?

Учитесь с помощью полной программы обучения математике K-5

Что такое математическая формула?

Формула факт или правило, написанное математическими символами. Обычно он связывает две или более величины знаком равенства. Когда вы знаете значение одной величины, вы можете найти значение другой, используя формулу.

Как найти площадь прямоугольника?

Площадь прямоугольника (A) равна произведению его длины «a» и ширины или ширины «b». Так, Площадь прямоугольника = (a × b) квадратных единиц.

Как найти длину и ширину, если у вас есть площадь и периметр?

Формула для периметра «P» прямоугольника, длина и ширина которого равны «l» и «w» соответственно, равна P = 2 (l + w). Чтобы сначала вычислить длину и ширину прямоугольника, вычислите значение ширины ‘w’, используя формулу площади прямоугольника, а именно: ‘w = A / l’.

Как ученики запоминают площадь и периметр?

Студенты также нарисуйте прямоугольник в своем математическом журнале и напишите слово «периметр» по всему периметру… снова и снова для моих друзей мелким почерком. Мы также пишем ОБЛАСТЬ в наших журналах, и я позволяю им раскрашивать внутреннюю часть букв As и R, чтобы напомнить им, что эта область находится внутри.

Как виртуально обучать периметру и площади?

практикующий Район и Периметр

Как узнать площадь прямоугольника?

Чтобы найти площадь прямоугольника, мы умножьте длину прямоугольника на ширину прямоугольника.

Какое правило для площади?

Правило площади гласит, что Площадь любого треугольника равна половине произведения длин двух сторон треугольника, умноженного на синус угла между двумя сторонами..

Какие 3 типа уравнений?

Есть три основных формы линейных уравнений: форма точечного уклона, стандартная форма и форма пересечения уклона. Мы рассмотрим все три в этой статье.

Что такое процентная формула?

Процент можно рассчитать, разделив значение на общее значение, а затем умножив результат на 100. Формула, используемая для расчета процента: (значение / общее значение) × 100%.

Каковы четыре математических правила?

Четыре правила математики: сложение, вычитание, умножение и деление.

Источник