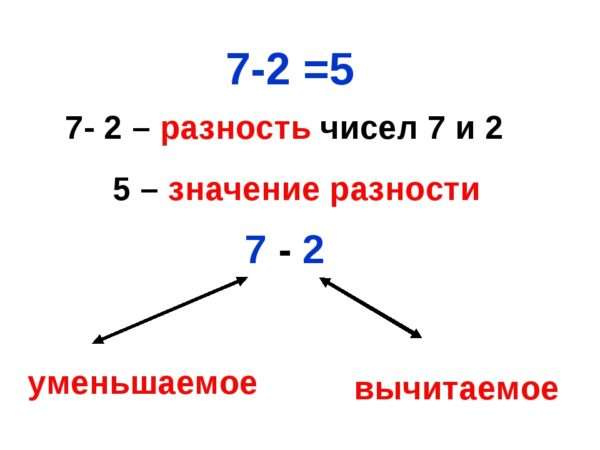
Как объяснить ребенку что такое сумма и разность чисел
Сумма и разность чисел
Что такое сумма, и как ее найти
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Как объяснить сложение и вычитание чисел?
Повторим важные математические действия в математике, такие как сложение и вычитание.
Сложение чисел
Сложение — это математическое действие. Числа, которые складываются, называются слагаемыми. Результат сложения называется суммой.
Чтобы найти сумму двух чисел, можно воспользоваться числовой прямой. Это самый простой способ. Числа располагают вдоль прямой линии, что позволяет легко считать их влево и вправо. На рисунке показано, как сложить числа 1 и 3.
Как объяснить?
На числовой прямой, чтобы найти сумму 1 и 3, встанем на отметку 1 и сделаем три шага вправо, добавляя по единице. В результате
мы окажемся на отметке 4. Это и будет ответ.
Что это значит?
Если мы прибавим 3 к 1, получим 4. Иначе говоря, сумма 1 и 3 равна 4.
Сложение многозначных чисел
Числа, которые состоят из нескольких цифр, складываются поразрядно: сначала единицы, затем десятки, потом сотни и т. д. Сумма каждого разряда записывается под ним.
Если сумма состоит из двух цифр, то старшая цифра переносится в следующий разряд.
Вычитание чисел
Вычитая одно число из другого, мы находим разницу между ними. Результат называется разностью.
Для вычитания также можно использовать числовую прямую.
Для этого делаем от отметки первого числа столько шагов влево, сколько единиц во втором числе. Здесь из 4 вычитаем 3.
Как объяснить?
На числовой прямой, чтобы вычесть 3 из 4, от отметки числа 4 сделаем три шага влево: сначала к 3, потом к 2 и, наконец, к отметке 1.
Что это значит?
Результат вычитания 3 из 4 равен 1. Иными словами, разность 4 и 3 равна 1.
Вычитание многозначных чисел
Числа, которые состоят из нескольких цифр, вычитаются поразрядно: сначала единицы, затем десятки, потом сотни и т. д. При этом иногда приходится заимствовать единицу из следующего (старшего) разряда.
Удивительно легкий способ обучения ребенка устному счету
Как научить ребенка устному счету

Почему я называю свой способ легким и даже удивительно легким? Да просто потому, что более простого и надежного способа обучения малышей счету я пока не встречал. Вы сами в этом скоро убедитесь, если воспользуетесь им для обучения своего ребенка. Для ребенка это будет просто игрой, а все, что потребуется от родителей — это уделять этой игре по несколько минут в день, и если будете придерживаться моих рекомендаций, то раньше или позже ваш ребенок обязательно начнет считать наперегонки с вами. Но возможно ли такое, если ребенку всего три или четыре года? Оказывается, вполне возможно. Во всяком случае, я успешно делаю это более десяти лет.
Весь процесс обучения я излагаю далее очень подробно, с детальным описанием каждой обучающей игры, для того чтобы его смогла повторить со своим ребенком любая мама. А, кроме того, в интернете на моем сайте «Семь ступенек к книжке» я разместил видеозаписи фрагментов моих занятий с детьми, чтобы сделать эти уроки еще более доступными для воспроизведения.
Сначала несколько вступительных слов.
Первый вопрос, который возникает у некоторых родителей: а стоит ли начинать учить ребенка счету до школы?
Я считаю, что обучать ребенка нужно тогда, когда он проявляет интерес к предмету обучения, а не после того, как этот интерес у него угас. А интерес к счету и подсчитыванию проявляется у детей рано, его надо лишь слегка подпитывать и незаметно день ото дня усложнять игры. Если же ваш ребенок почему-то безразличен к пересчитыванию предметов, не говорите себе: «У него нет склонности к математике, я тоже в школе по математике отставала». Постарайтесь пробудить в нем этот интерес. Просто включите в его развивающие игры то, что вы до сих пор упускали: пересчитывание игрушек, пуговичек на рубашке, ступенек при ходьбе и т.п.
Второй вопрос: каким способом лучше обучать ребенка?
Ответ на этот вопрос вы получите, прочитав здесь полное изложение моей методики обучения устному счету.
Как правильно научить ребенка складывать и вычитать
А пока хочу предостеречь вас от применения некоторых способов обучения, не приносящих ребенку пользу.
Не учите ребенка складывать и вычитать по единице:
«Чтобы к прибавить 3, нужно сначала к прибавить 1, получится 3, потом к прибавить еще 1, получится 4, и, наконец, к прибавить еще 1, в результате будет 5»; «- Чтобы от отнять 3, нужно сначала отнять 1, останется 4, потом от отнять еще 1, останется 3, и, наконец, от отнять еще 1, в результате останется 2».
Этот, к сожалению, распространенный способ вырабатывает и закрепляет привычку к медленному подсчитыванию и не стимулирует умственное развитие ребенка. Ведь считать — значит складывать и отнимать сразу целыми числовыми группами, а не добавлять и убавлять по единичке, да еще и с помощью пересчитывания пальчиков или палочек. Почему же этот не полезный для ребенка способ так распространен? Думаю, потому что так проще учителю. Надеюсь, что некоторые учителя, ознакомившись с моей методикой, откажутся от него.
Не начинайте учить ребенка считать с помощью палочек или пальцев и следите, чтобы он не начал пользоваться ими позже по совету старшей сестрички или братика. Научить считать на пальцах легко, а отучить трудно. Пока ребенок считает по пальцам, механизм памяти не задействован, в памяти не откладываются результаты сложения и вычитания целыми числовыми группами.
И, наконец, ни в коем случае не используйте появившийся в последние годы способ счета «по линеечке»:
«Чтобы к прибавить 3, нужно взять линеечку, найти на ней цифру 2, отсчитать от нее вправо 3 раза по сантиметру и прочитать на линеечке результат 5»;
«Чтобы от отнять 3, нужно взять линеечку, найти на ней цифру 5, отсчитать от нее влево 3 раза по сантиметру и прочитать на линеечке результат 2».
Этот способ счета с использованием такого примитивного «калькулятора», как линеечка, как будто нарочно придуман для того, чтобы отучить ребенка думать и запоминать. Чем так учить считать, лучше вовсе не учить, а сразу показать, как пользоваться калькулятором. Ведь этот способ, точно так же, как и калькулятор, исключает тренировку памяти и тормозит умственное развитие малыша.
С чего начать обучение счету
На первом этапе обучения устному счету необходимо научить ребенка считать в пределах десяти. Нужно помочь ему прочно запомнить результаты всех вариантов сложения и вычитания чисел в пределах десяти так, как помним их мы, взрослые.
На втором этапе обучения дошкольники осваивают основные методы сложения и вычитания в уме двузначных чисел. Главным теперь уже является не автоматическое извлечение из памяти готовых решений, а понимание и запоминание способов сложения и вычитания в последующих десятках.
Как на первом, так и на втором этапе обучение устному счету происходит с применением элементов игры и состязательности. С помощью обучающих игр, выстроенных в определенной последовательности, достигается не формальное заучивание, а осознанное запоминание с использованием зрительной и тактильной памяти ребенка с последующим закреплением в памяти каждого усвоенного шага.
Почему я учу именно устному счету? Потому что только устный счет развивает память, интеллект ребенка и то, что мы называем смекалкой. А именно это и потребуется ему в последующей взрослой жизни. А писание «примеров» с длительным обдумыванием и вычислением ответа на пальчиках дошкольнику ничего, кроме вреда, не приносит, т.к. отучает думать быстро. Примеры он будет решать позже, в школе, отрабатывая аккуратность оформления. А сообразительность необходимо развить в раннем возрасте, чему способствует именно устный счет.
Еще до того как начать обучение ребенка сложению и вычитанию, родители должны научить его пересчитывать предметы на картинках и в натуре, считать ступеньки на лестнице, шаги на прогулке. К началу обучения устному счету ребенок должен уметь сосчитать хотя бы пять игрушек, рыбок, птичек, или божьих коровок и при этом освоить понятия «больше» и «меньше». Но все эти разнообразные предметы и существа не следует использовать в дальнейшем для обучения сложению и вычитанию. Обучение устному счету нужно начинать со сложения и вычитания одних и тех же однородных предметов, образующих определенную конфигурацию для каждого их числа. Это позволит задействовать зрительную и тактильную память ребенка при запоминании результатов сложения и вычитания целыми числовыми группами (см. видеофайл 056). В качестве пособия для обучения устному счету я применил набор небольших счетных кубиков в коробочке для счета (подробное описание — далее). А к рыбкам, птичкам, куклам, божьим коровкам и прочим предметам и существам дети вернутся позже, при решении арифметических задач. Но к этому времени сложение и вычитание любых чисел в уме уже не будет представлять для них сложности.
Для удобства изложения я разбил первый этап обучения (счет в пределах первого десятка) на 40 уроков, а второй этап обучения (счет в последующих десятках) еще на Пусть вас не пугает большое количество уроков. Разбивка всего курса обучения на уроки приблизительна, с подготовленными детьми я прохожу иногда по урока за одно занятие, и вполне возможно, что вашему малышу так много занятий не потребуется. Кроме того, уроками эти занятия можно назвать лишь условно, т.к. продолжительность каждого составляет лишь Их можно также совмещать с уроками чтения. Заниматься желательно два раза в неделю, а выполнению домашних заданий достаточно уделять по минут в остальные дни. Самый первый урок нужен не каждому ребенку, он разработан лишь для детей, которые еще не знают цифры 1 и, глядя на два предмета, не могут сказать, сколько их, не подсчитав предварительно пальчиком. Их обучение необходимо начинать практически «с чистого листа». Более подготовленные дети могут начинать сразу со второго, а некоторые — с третьего или четвертого урока.
Я провожу занятия одновременно с тремя детьми, не более, чтобы удерживать внимание каждого из них и не давать им скучать. Когда уровень подготовки детей несколько отличается, приходится заниматься с ними поочередно разными задачками, все время переключаясь с одного ребенка на другого. На начальных уроках присутствие родителей желательно для того, чтобы они поняли суть методики и правильно выполняли несложные и коротенькие ежедневные домашние задания со своими детьми. Но разместить родителей надо так, чтобы дети забыли об их присутствии. Родители не должны вмешиваться и одергивать своих детей, даже если те шалят или отвлекаются.
Занятия с детьми устным счетом в небольшой группе можно начинать, приблизительно, с трехлетнего возраста, если они уже умеют подсчитывать пальчиком предметы, хотя бы до пяти. А с собственным ребенком родители вполне могут заниматься начальными уроками по этой методике и с двух лет.
Как научить ребенка счету в пределах пяти
Для проведения начальных уроков потребуются пять карточек с цифрами 1, 2, 3, 4, 5 и пять кубиков с размером ребра примерно установленных в коробочке. В качестве кубиков я использую продающиеся в магазинах развивающих игр «кубики знаний», или «learning bricks», по 36 кубиков в коробке. На весь курс обучения вам потребуются три таких коробки, т.е. 108 кубиков. Для начальных уроков я беру пять кубиков, остальные понадобятся позже. Если вам не удастся подобрать готовые кубики, то их несложно будет изготовить самостоятельно. Для этого нужно лишь распечатать на плотной бумаге, рисунок, а затем вырезать из него заготовки кубиков, склеить их в соответствии с имеющимися указаниями, заполнить любым наполнителем, например, какой-нибудь крупой, и оклеить снаружи скотчем. Необходимо также изготовить коробочку для установки этих пяти кубиков в ряд. Склеить ее так же просто из распечатанного на плотной бумаге и вырезанного рисунка. На дне коробочки начерчены пять клеток по размеру кубиков, кубики должны помещаться в ней свободно.
Вы уже поняли, что обучение счету на начальном этапе будет производиться с помощью пяти кубиков и коробочки с пятью клетками для них. В связи с этим возникает вопрос: а чем же способ обучения с помощью пяти счетных кубиков и коробочки с пятью клетками лучше обучения при помощи пяти пальцев? Главным образом тем, что коробочку учитель время от времени может накрывать ладонью или убирать, благодаря чему расположенные в ней кубики и пустые клетки очень скоро запечатлеваются в памяти ребенка. А пальцы ребенка всегда остаются при нем, он может их увидеть или нащупать, и в запоминании просто не возникает необходимости, стимулирование механизма памяти не происходит.
Не следует также пытаться заменять коробочку с кубиками счетными палочками, другими предметами для счета или кубиками, не составленными в коробочке в ряд. В отличие от кубиков, выстроенных в ряд в коробочке, эти предметы располагаются беспорядочно, не образуют постоянной конфигурации и потому не откладываются в памяти в виде запомнившейся картинки.
Урок № 1: первые игры для обучения счету
До начала урока выясните, какое количество кубиков ребенок способен определять одновременно, не пересчитывая их по штучке пальчиком. Обычно к трем годам дети могут сказать сразу, не подсчитывая, сколько в коробке кубиков, если их количество не превышает двух или трех, и лишь некоторые из них видят сразу четыре. Но есть дети, которые пока могут назвать лишь один предмет. Для того чтобы сказать, что видят два предмета, они должны посчитать их, показывая пальчиком. Для таких детей и предназначен первый урок. Остальные присоединятся к ним позже. Чтобы определить, какое количество кубиков ребенок видит сразу, ставьте попеременно в коробочку разное количество кубиков и спрашивайте: «Сколько кубиков в коробочке? Не считай, скажи сразу. Молодец! А сейчас? А сейчас? Правильно, молодец!» Дети могут сидеть или стоять у стола. Коробочку с кубиками ставьте на стол рядом с ребенком параллельно кромке стола.
Для выполнения заданий первого урока оставьте детей, которые пока могут определить только один кубик. Играйте с ними поочередно.
Потом усложните игру. Скажите: «А теперь сделаем домику крышу». Накройте коробочку ладонью и повторите игру. Каждый раз, когда ребенок скажет, сколько гномиков стало в домике, после того как один пришел, или сколько их в нем осталось, после того как один ушел, убирайте крышу-ладонь и позволяйте ребенку самому добавлять или убирать кубик и убеждаться в правильности своего ответа. Это способствует подключению не только зрительной, но и тактильной памяти ребенка. Убирать всегда нужно последний кубик, т.е. второй слева.
Играйте в игры 1 и 2 поочередно со всеми детьми в группе. Скажите родителям, присутствующим на уроке, что дома они должны играть со своими детьми в эти игры ежедневно один раз в день, если только дети сами не просят больше.
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
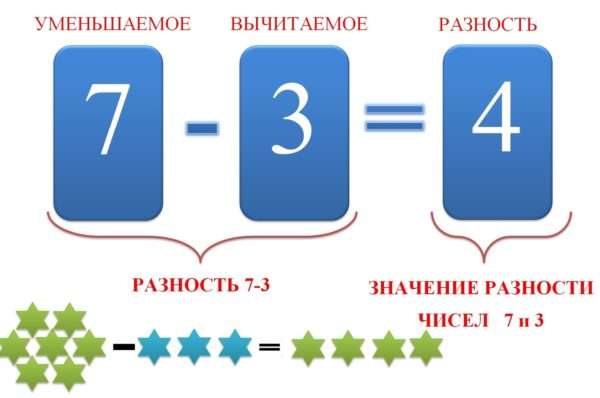
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.