Как определить что точки лежат на одной прямой

Как определить, лежат ли точки на одной прямой

Если вам даны две точки, то вы можете смело заявить, что они лежат на одной прямой, так как через любые две точки можно провести прямую. Но как же выяснить, лежат ли все точки на прямой, если точек три, четыре или больше? Доказать принадлежность точек одной прямой можно несколькими способами.Вам понадобится

Если вам даны точки с координатами (х1, у1, z1), (х2, у2, z2), (х3, у3, z3), найдите уравнение прямой, используя координаты любых двух точек, например, первой и второй. Для этого подставьте соответствующие значения в уравнение прямой: (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Если один из знаменателей равен нулю, просто приравняйте к нулю числитель.

Найти уравнение прямой, зная две точки с координатами (х1, у1), (х2, у2), еще проще. Для этого подставьте значения в формулу (х-х1)/(х2-х1)=(у-у1)/(у2-у1).

Получив уравнение прямой, проходящей через две точки, подставьте значения координат третьей точки в него вместо переменных х и у. Если равенство получилось верное, значит все три точки лежат на одной прямой. Точно так же можете проверять принадлежность этой прямой других точек.

Проверьте принадлежность всех точек прямой, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли верным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.

Чтобы найти решение задачи графическим способом, постройте координатные плоскости и найдите точки по указанным координатам. Затем проведите прямую через две из них и продолжите до третьей точки, посмотрите, пройдет ли она через нее. Учтите, этот способ подходит только для точек, заданных на плоскости с координатами (х, у), если же точка задана в пространстве и имеет координаты (х, у, z), то такой способ неприменим.

Источник

Когда 3 точки лежат на одной прямой

Очень часто при решения домашней работы возникает вопрос: когда 3 точки лежат на одной прямой, ответ очень прост и он лежит в основе геометрии.

Осуществить проверку того, что три точки лежат на одной прямой можно через составления уравнения, рассматриваемой прямой, которая проходит через две наугад выбранные точки из этих трех. И проверки того, что этому уравнению удовлетворяют координаты оставшейся из этих трех точек.

Есть разные виды уравнения прямой. Воспользуемся одним из простейших способов и рассмотрим его для конкретно заданных точек.

Это сделаем лишь для того, чтобы не решать поставленную задачу в общем виде, а чтобы дать ответ на вопрос лежат ли 3 именно эти точки с этими координатами на одной прямой. Сформулируем задачу: Необходимо проверить лежат ли точки A(-2;1), Б(0;3), В (5;-7) на одной прямой.

Решим поставленную задачу

Как известно, через любые две точки можно провести прямую, причем единственную. Вот и проведем мысленно эту прямую. Допустим, прямую АБ. Значит, решение нашей задачи свелось к тому, что нужно проверить: принадлежит ли точка В прямой АБ. Если окажется, что точка В принадлежит прямой АБ, то все точки из условия будут лежать на одной прямой. Если мы выясним, что точка В не принадлежит прямой АБ, то можно будет утверждать, что точки А, Б и В на одной прямой не лежат. Составим уравнение прямой АБ как уравнение прямой проходящей через две точки:

После преобразования получим:

Как видим, не получили верное числовое равенство. Значит в этом случае точки А, Б, В не лежат на одной прямой.

Пример, когда 3 точки лежат на одной прямой можно легко подобрать для этой задачи. Всего лишь точка В должна иметь координаты (0;3) или (-7;-4)

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Как определить что точки лежат на одной прямой

Если три точки A, B и C лежат на одной прямой, то треугольник ABC обратится в отрезок прямой, а потому его площадь должна быть равна нулю. Полагая в формуле

S = 0, получим условие, при котором три точки лежат на одной прямой

В более удобной форме условие, при котором три точки лежат на одной прямой, можно записать так:

(1)

Подставляя сюда координаты данных точек, получим, что левая часть (1) будет равна

Требование (1) выполнено:

и, значит, три данные точки лежат на одной прямой.

Источник

Как определить, лежат ли точки на одной прямой

Вам понадобится

Инструкция

Совет 2: Как проверить, что точки не лежат на одной прямой

Вам понадобится

Инструкция

5. Разглядите 2-й вариант определения принадлежности точки примой: на данный раз надобно проверить принадлежит ли точка С(x,y) отрезку с концевыми точками В(x1,y1) и А(x2,y2), тот, что является частью прямой z.

6. Точки рассматриваемого отрезка опишите уравнением pOB+(1-p)OА=z, при условии, что 0?p?1. ОВ и ОА являются векторами. Если есть такое число p, которое огромнее либо равно 0, но поменьше либо равно 1, то pOB+(1-p)OА=С, а значит, точка С будет лежать на отрезке АВ. В отвратном случае, данная точка не будет принадлежать этому отрезку.

7. Распишите равенство pOB+(1-p)OА=С покоординатно: px1+(1-p)x2=x и py1+(1-p)y2=y.

8. Обнаружьте из первого уравнения число р и подставьте его значение во второе равенство. Если равенство будет соответствовать условиям 0?p?1, то точка С принадлежит отрезку АВ.

Обратите внимание!
Удостоверитесь в правильности расчетов!

Полезный совет
Дабы обнаружить k – угловой показатель прямой, надобно (y2 – y1)/(x2 – x1).

Совет 3: Как провести прямую через две точки

Построение прямых — основа технического черчения. Теперь это все почаще делается с поддержкой графических редакторов, которые предоставляют проектировщику крупные вероятности. Впрочем некоторые тезисы построения остаются теми же, что и в классическом черчении – с подмогой карандаша и линейки.

Вам понадобится

Инструкция

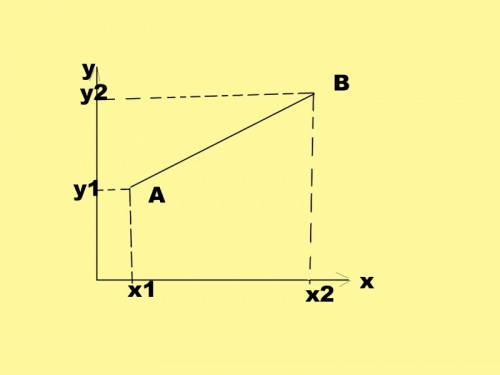
1. Начните с классического построения. Определите плоскость, в которой вы будете строить прямую. Пускай это будет плоскость листа бумаги. В зависимости от условий задачи расположите точки. Они могут быть произвольными, но не исключено, что задана какая-то система координат. Произвольные точки поставьте там, где вам огромнее понравится. Обозначьте их как А и В. С поддержкой линейки объедините их. Согласно аксиоме, через две точки неизменно дозволено провести прямую, притом только одну.

2. Начертите систему координат. Пускай вам даны координаты точки А (х1; у1). Дабы их обнаружить, нужно отложить по оси х надобное число и провести через подмеченную точку прямую, параллельную оси у. После этого отложите величину, равную у1, по соответствующей оси. Из подмеченной точки проведите перпендикуляр до его пересечения с первым. Место их пересечения и будет точкой А. Таким же образом обнаружьте точку В, координаты которой дозволено обозначить как (х2; у2). Объедините обе точки прямой.

3. В программе AutoCAD прямую дозволено возвести несколькими методами. Функция «по двум точкам» обыкновенно установлена по умолчании. Обнаружьте в верхнем меню вкладку «Основная». Вы увидите перед собой панель «Рисование». Обнаружьте кнопку с изображением прямой линии и нажмите на нее.

4. Прямую по двум точкам в этой программе дозволено возвести двумя методами. Поставьте курсор в надобную точку на экране и щелкните левой кнопкой мыши. После этого определите вторую точку, протяните туда линию и тоже щелкните мышкой.

5. AutoCAD разрешает также задать координаты обеих точек. Наберите в находящейся внизу командной строке (_xline). Нажмите Enter. Введите координаты первой точки и тоже нажмите на ввод. Верно также определите и вторую точку. Ее дозволено указать и щелчком мыши, поставив курсор в необходимую точку экрана.

6. В AutoCAD дозволено возвести прямую не только по двум точкам, но и по углу наклона. В контекстном меню «Рисование» выберите прямую, а после этого опцию «Угол». Начальную точку дозволено поставить щелчком мыши либо по координатам, как и в предыдущем методе. После этого задайте размер угла и нажмите на ввод. По умолчании прямая расположится под необходимым углом к горизонтали.

Видео по теме

Совет 4: Как подтвердить, что точка не лежит в плоскости треугольника

Подтвердить, что точка не лежит в плоскости треугольника, дозволено легкой проверкой всех допустимых обстановок, тем больше что их не много. Не следует только забывать, что дозволено придти и к событию противоположному, то есть случаю, когда точка является внутренней для заданного треугольника.

Инструкция

1. Раньше чем искать решение поставленной задачи, читателю следует самому принять решение о принадлежности сторон треугольника. Считать их точки внешними для треугольника либо нет. На данной стадии считаем, что это область замкнутая, а следственно она включает свои границы. Для простоты разглядите «плоский случай», но не забывайте и о пространственном обобщении. Следственно типовые уравнения для прямых плоскости вида y=kx+b, применять не следует, по весьма мере в начале решения.

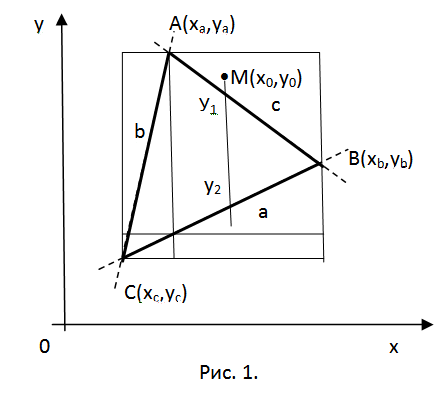
2. Выберите метод задания для сторон треугольника. Судя по постановке задачи, это не имеет твердого значения. Следственно считайте, что даны координаты его вершин A(xa, ya), B(xb, yb), C(xc, yc) (см. рис. 1.). Обнаружьте направляющие векторы сторон треугольника AB=, BC=, AC= и запишите канонические уравнения прямых, содержащих эти стороны. Для AB – (x-xa)/(xb-xa)=(y-ya)/(yb-ya). Для BС – (x-xb)/(xc-xb)=(y-yb)/(yc-ya). Для AС – (x-xa)/(xc-xa)=(y-ya)/(yc-ya). В соответствии с рисунком проведите горизонтальные и вертикальные линии, которые дозволено записать как x=xc, x= xa, x=xb, y=yc, y=ya, y=yb. Это дозволит до минимума сократить число вычислений. Дальше следуйте предложенному алгорифму. На рисунке заданная точка М(xo,yo) помещена в самом «неблагополучном» месте.

3. Следуя по оси 0х, проверьте выполнение неравенства xc?xo?хb. Если оно не исполнено, то точка теснее лежит вне пределов треугольника, потому что «не внутри» – это и есть «снаружи». Если же неравенство исполнено, то дальше проверьте честность xc

4. Проверьте выполнение неравенства уc?уo?уа. Если оно не объективно, то точка не лежит внутри треугольника. В отвратном случае обнаружьте ординату прямой, содержащей АB. у1=y(xo)=[(yb-ya)(xo-xa)]/(xb-xa)+ya. Также поступите с ординатой прямой для BC. у2=у(хо)=[(yс-yb)(xo-xb)]/(xc-xb)+yc. Составьте неравенство y2?yo?y1. Его выполнение разрешает сделать завершение о том, что заданная точка находится внутри треугольника. Если же это неравенство ложно, то она лежит вне его пределов, в частности в соответствии с рисунком.

Источник