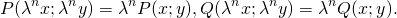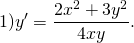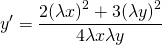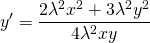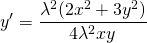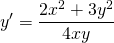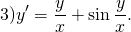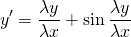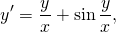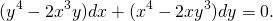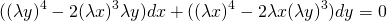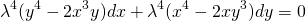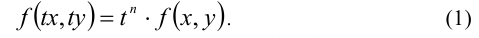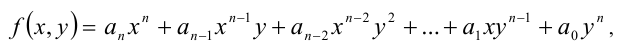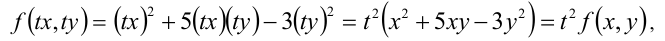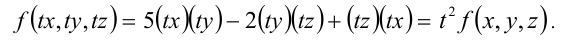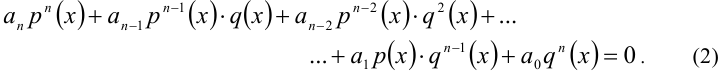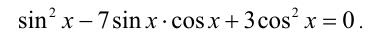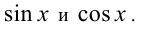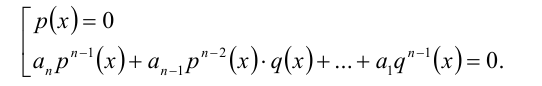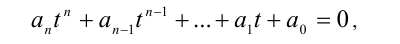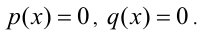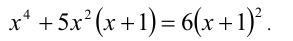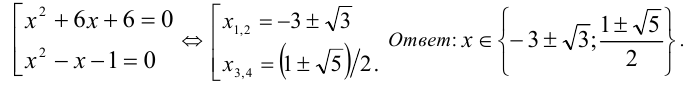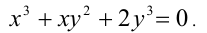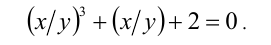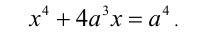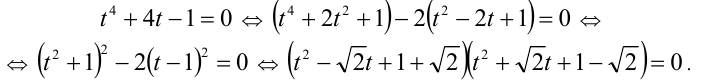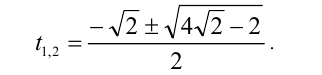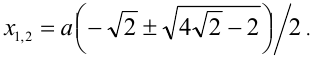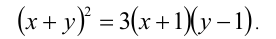Как определить что уравнение однородное
Как определить однородное уравнение
Дифференциальное уравнение 1-го порядка P(x;y)dx+Q(x;y)dy=0 называется однородным, если P(x;y) и Q(x;y) — однородные функции одинакового измерения, то есть
Как определить, что дифференциальное уравнение — однородное? На практике проверку уравнения на однородность проводят следующим образом: вместо каждого x подставляют λx, вместо каждого y — λy. При этом y’, dx и dy не трогают. После этого упрощают уравнение. Если после упрощения удается сократить на λ (или n- ю степень λ) и получить исходное уравнение, то это и означает, что данное уравнение является однородным уравнением 1-го порядка.
Другая форма записи: y’=f(x;y). Это уравнение является однородным, если функция f(x;y) является однородной функцией нулевого порядка. Это означает, что f(λx;λy)=f(x;y).
Подставляем вместо каждого x λx, вместо каждого y — λy:
Выносим лямбда в квадрате за скобки и сокращаем на него:
Пришли к исходному уравнению, а это значит, что данное уравнение — однородное.
2) (x-y)ydx-x²dy=0.
Подставляем вместо каждого x λx, вместо каждого y — λy: (λx-λy)λydx-(λx)²dy=0. Теперь выносим общий множитель λ² за скобки: λ²((x-y)ydx-x²dy)=0. Делим обе части уравнения на λ²:
(x-y)ydx-x²dy=0. Пришли к исходному уравнению, значит, это уравнение — однородное. (Здесь P(x;y) и Q(x;y) — однородные функции 2й степени).
Наличие дроби y/x уже косвенно указывает на то, что уравнение может быть однородным. Проверим, так ли это:
После сокращения на λ получаем исходное уравнение:
а это значит, что данное уравнение является однородным.
Подставляем вместо каждого x λx, вместо каждого y — λy:
Делим обе части уравнения на лямбда в 4й степени:
Получили исходное уравнение, а значит, оно является однородным. (Здесь P(x;y) и Q(x;y) — однородные функции 4й степени).
Дифференциальное однородное уравнение: особенности и решение
Однородные уравнения
| F = | g 3 +r 3 | A = | d 2 + w 2 |
| 3g 3 + 5r 2 g | 2dw |
Чтобы убедиться в их однородности, достаточно аргументы функции F или A умножить на какой-либо коэффициент и посмотреть, не сократится ли он.
Замена e(t) = f(1, t)
Выше говорилось о том, что дифференциальные уравнения с однородными функциями сводятся к разделяющимся за счет замены. Для объяснения этого рассмотрим лемму.
Доказывается данная лемма тривиальным образом: для этого просто нужно положить k = 1/x для всех ненулевых x.
Применение замены в решение y’ = f(x, y)
Интегрируя, получим решение E = ln|x| + C.
Заметка
Рассмотрим, почему вышеописанная замена работает при решении однородных дифференциальных уравнений. Для этого возьмем общее решение E = ln|x| + C и заменим x на kx и y на ky: E = ln|kx| + C = ln(k) + ln|x| + C. В свою очередь выражение ln(k) + C может быть представлено как W, и тогда решение будет выглядеть как E = ln|x| + W.
Получается, что замена x на kx и y на ky приводит лишь к замещению одного решения другим, но из того же класса. Иными словами, другое решение также удовлетворяет исходному уравнению. Описанное свойство на координатной плоскости называется гомотетией, т. е. интегральные кривые однородных дифференциальных уравнений переходят друг в друга.
Пример 1
Дано уравнение l 2 + ml + m 2 l’ + m 2 = 0. Найдем его решение. Неопытный глаз может по ошибке торопливо заключить, что данное уравнение не однородно, так как подстановка km вместо m и kn вместо n не дает исходное уравнение. Ошибка в данном случае заключается в том, что уравнение предварительно не было разрешено относительно производной n’. Сделаем.
В данном виде легко определить, что уравнение однородно.
| f(km, kl) = | (-1)[(km) 2 + (kl) 2 + k 2 ml] | = | (-1)(l 2 +ml+m 2 )k 2 | = | f(m, l) |
| (km) 2 | m 2 k 2 |
Приступим к решению, совершив замену l/m = v. Получим l = vm и l’ = mv’ + v. Подставим эти значения в уравнение:
Из получившегося уравнения в дифференциальной форме легко находится общий интеграл:
Проведем обратную замену:
Линейные дифференциальные уравнения
Часто однородные дифференциальные уравнения путают с линейными. Для полноты вопроса рассмотрим немного и этот класс. Итак, линейным называется дифференциальное уравнение, в котором функция и ее производная располагаются в линейной зависимости, т. е. получаем уравнение, которому присущ следующий вид:
Для разрешения этого уравнения относительно y’ необходимо рассмотреть все корни o(x). Положим, что для некоторого числа o(x0) = 0, тогда одним из решений описанного уравнение будет x0, т.к. получаем o(x0)dy = 0 и dx = 0. Это становится очевидным, если записать дифференциальную форму уравнения, умножив на dx обе части: o(x)dy + w(x)ydx = e(x)dx.
Исключив нулевые значения o(x), для оставшихся значений x записываем уравнение в разрешенном виде, поделив его на o(x).
Решение линейных дифференциальных уравнений
В общем случае линейное уравнение (неоднородное) решается в несколько этапов:
Еще одна путаница однородных уравнений возникает при рассмотрении однородных систем уравнений. Однако это другой вопрос, рассмотрение которого выходит за пределы данной статьи.
Примеры
Дана задача. Нужно найти решение.
| y’ + | ty | = | t |
| t 2 +1 | √(t 2 +1) |
Очевидно, данное уравнение неоднородно, поэтому решим сначала следующее уравнение:
Следует отметить, что одним из решений уравнения является y = 0. Нахождение общего решения происходит через дифференциальную форму, которая позволяет воспользоваться разделением переменных:
| dy | = | (-1)tdt |
| y | t 2 +1 |
Решение неоднородного уравнения выполним другим, аналогичным способом, который называется методом вариации постоянной, или метод Лагранжа. Опишем его теоретически.
Применяя метод Лагранжа для нашей задачи, положим:
| y | = | x 2 | + | D |
| 2√(t 2 +1) | √(t 2 +1) |
Мы рассмотрели способы решения линейных однородных уравнений.
Линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения 2-го порядка
Линейные однородные дифференциальные уравнения (ЛОДУ) 

Частным случаем дифференциальных уравнений (ДУ) такого типа называют линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.
Общее решение линейного однородного дифференциального уравнения 

Самое сложное заключается в определении линейно независимых частных решений ДУ такого типа. Зачастую, частные решения выбирают из таких систем линейно независимых функций:
Но достаточно редко частные решения представляются именно так.
Примером линейного однородного дифференциального уравнения можно назвать 
Общее решение линейного неоднородного дифференциального уравнения 

где y0 является общим решением соответствующего линейного однородного дифференциального уравнения,
а 

Как пример линейного неоднородного дифференциального уравнения приводим 
Познакомиться ближе с теорией и просмотреть примеры решений можете здесь: Линейные дифференциальные уравнения второго порядка.
Однородные уравнения
Однородные уравнения
Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде
где 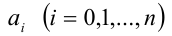
т.е. условие (1) из определения выполняется (n = 2).
Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.
Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве, 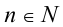
В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида
Оно является однородным тригонометрическим уравнением 2-й степени относительно функций
Перейдём к процедуре решения уравнения (2).
Если хотя бы один из коэффициентов 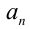
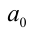
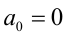
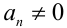
Если же 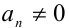
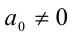
решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.
2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений
Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.
Пример №185.
Решить уравнение
Решение:
Пример №186.
Решить в целых числах уравнение
Решение:
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть 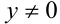
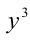
Ответ: 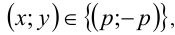
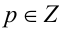
Пример №187.
Для каждого действительного значения параметра а решить уравнение
Решение:
Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.
2) Если 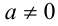
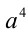
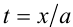
Первый сомножитель в нуль не обращается, а второй имеет два корня
Ответ: при а = 0 единственное решение x = 0 ;
при 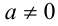
Пример №188.
Найти действительные корни уравнения
Решение:
Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду
Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.
1) Если 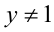
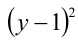
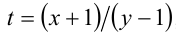
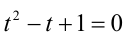
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Однородное уравнение
Смотреть что такое «Однородное уравнение» в других словарях:
однородное уравнение — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN homogeneous equation … Справочник технического переводчика
Однородное уравнение — Однородным уравнением n й степени, называется уравнение вида: Такое уравнение после исключения отдельно рассматриваемого случая и деления уравнения на сводится с помощью замены к алгебраическому уравнению … Википедия
Уравнение Коши — Эйлера — В математике ( дифференциальных уравнениях), уравнение Коши Эйлера (Эйлера Коши) является частным случаем линейного дифференциального уравнения (см. линейное дифференциальное уравнение), приводимым к линейному дифференциальному уравнению с… … Википедия
Уравнение теплопроводности — Пример численного решения уравнения теплопроводности. Цветом и высотой поверхности передана температура данной точки. Уравнение теплопроводности важное уравнение в частных производных, которое описывает распространение тепла в заданной… … Википедия
Уравнение Коши — В математике (дифференциальных уравнениях), уравнение Коши Эйлера (Эйлера Коши) является частным случаем линейного дифференциального уравнения (см. линейное дифференциальное уравнение), приводимым к линейному дифференциальному… … Википедия
Уравнение диффузии — Механика сплошных сред … Википедия
Линейное дифференциальное уравнение с постоянными коэффициентами — Линейное дифференциальное уравнение с постоянными коэффициентами обыкновенное дифференциальное уравнение вида: где искомая функция, её тая производная, фиксированные числа … Википедия