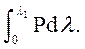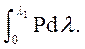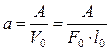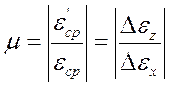Как определяется и что характеризует удельная работа

Работа деформации

Кроме уже названных характеристик механических свойств материа-ла диаграмма растяжения позволяет определить еще и энергетические его характеристики.

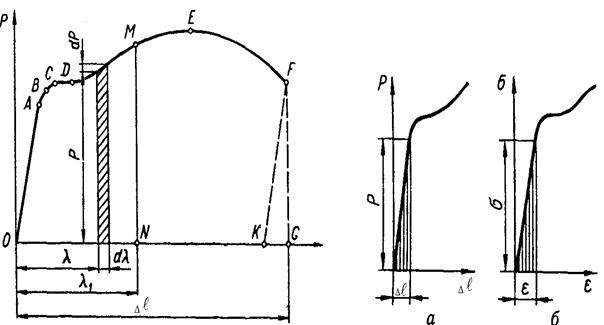
Площадь диаграммы растяжения в координатах Р-D 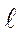характери-зует работу, израсходованную на разрыв образца. Пусть некоторой растягивающей силе Р отвечает деформация λ образца (рис. 2.5). При бесконечно маленьком приросте dА прирост деформации будет dλ. Работа внешних сил на этом перемещении

Рисунок 2.5 Рисунок 2.6

Работа, которая израсходована при растяжении образца на удлине-ние λ₁, будет равна:

А =

Из рисунка 2.5 видно, что работа, израсходованная на разрыв образ-ца, будет равняться всей площади OABCDEFGO диаграммы растяжения. В пределах упругости полная работа деформации определяется площадью треугольника (рис.2.6, а):

А_пр = 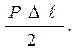(2.17)

где V = F_{0 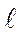0},

тогда а _пр = 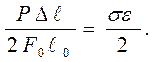(2.18)

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Работа деформации

Кроме уже названных характеристик механических свойств материа-ла диаграмма растяжения позволяет определить еще и энергетические его характеристики.

Площадь диаграммы растяжения в координатах Р-D характери-зует работу, израсходованную на разрыв образца. Пусть некоторой растягивающей силе Р отвечает деформация λ образца (рис. 2.5). При бесконечно маленьком приросте dА прирост деформации будет dλ. Работа внешних сил на этом перемещении

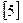
Рисунок 2.5 Рисунок 2.6

Работа, которая израсходована при растяжении образца на удлине-ние λ₁, будет равна:

А =

Из рисунка 2.5 видно, что работа, израсходованная на разрыв образ-ца, будет равняться всей площади OABCDEFGO диаграммы растяжения. В пределах упругости полная работа деформации определяется площадью треугольника (рис.2.6, а):

А_пр = 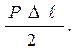(2.17)

где V = F_{0 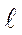0},

тогда а _пр = 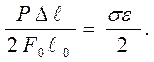(2.18)

Дата добавления: 2015-01-10 ; просмотров: 1518 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Большая Энциклопедия Нефти и Газа

Удельная работа деформации характеризует способность материала сопротивляться ударному действию нагрузки: чем больше удельная работа деформации до разрыва, тем лучше материал сопротивляется ударным нагрузкам. [1]

Удельная работа деформации является мерой энергетической емкости ( работоспособности) материала и может служить общей характеристикой его механических качеств. [2]

Удельная работа деформации характеризует способность материала сопротивляться ударному действию нагрузки: чем больше удельная работа деформации до разрыва, тем лучше материал сопротивляется ударным нагрузкам. [3]

Удельная работа деформации А есть положительно-определенная квадратичная форма ее аргументов; это значит, что она может принимать только положительные значения при каких бы то ни было вещественных значениях аргументов. Если должен превратиться в нуль интеграл ( 15), то и интегрируемая величина должна стать тождественно равной нулю, а это, как только-что отмечено, возможно только в том случае, когда все составляющие тензора деформации превращаются в нуль. Перемещения и, v, w представляют в таком случае движение тела, не сопровождающееся деформацией; при таком движении линейные элементы сохраняют свою длину; это есть не что иное как вращение твердого тела, связанное с поступательным перемещением. [4]

Удельная работа деформации а равна площади схематизированной диаграммы растяжения OS0Sk ( фиг. [5]

Удельная работа деформации характеризует способность материала сопротивляться ударному действию нагрузки: чем больше удельная работа деформации до разрыва, тем лучше материал сопротивляется ударным нагрузкам. [6]

Удельная работа деформации хрупких материалов мала. Этим объясняется слабое сопротивление таких материалов ударам и вообще динамическим нагрузкам. [7]

Следовательно, удельная работа деформации выражается величиной работы, потребной для доведения образца до разрыва, отнесенной к единице его объема. [8]

Это и есть удельная работа деформации формы элемента ( упругого тела), находящегося в пластическом состоянии. [9]

Во втором случае определяется удельная работа деформации А ( кГм / см3), равная работе, затраченной на разрушение от растяжения однократным ударом ненадрезанного образца, отнесенной ко всему деформированному объему образца. Эта величина характеризует способность материала выдерживать динамические нагрузки. [10]

Действительный предел прочности характеризует удельную работу деформации в граничном слое стружки, которая определяет температуру в зоне контакта обрабатываемого металла и инструмента, а также интенсивность износа инструмента. [11]

Формула (3.3) показывает, что удельная работа деформации измеряется величиной площади истинной диаграммы растяжения. [12]

Характеристическую энергию можно вычислить, зная удельную работу деформации Wv Последняя может быть вычислена или определена на опыте. [14]

Полученные нами выражения (3.112) и (3.113) для удельной работы деформации представляют замечательную аналогию с тем выражением удельной работы деформации, которое мы имеем в теории сопротивления материалов. [15]

Источник

УДЕЛЬНАЯ РАБОТА И МОЩНОСТЬ РЕЗАНИЯ.

Чтобы получить общую силу воздействия резца на древесину S, необходимо векторно сложить силы воздействия отдельных его участков: S=S_л+S_п+S₃. Силу S можно представить как векторную сумму (рисунки) общей касательной силы Р и общей нормальной силы Q: S=Р+Q. Силы Р и Q, действующие на древесину со стороны резца в целом, получаются сложением их составляющих, найденных для отдельных участков рабочей зоны резца : Р=Р_л+Р_п+Р₃;

Q=Q_л-Q_п+Q₃.

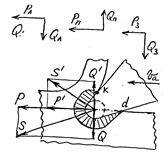
Выбор направлений для составляющих общей силы воздействия резца и его участков на древесину не случаен: сила, касательная к траектории определяет мощность, расходуемую на резание; нормальная сила передается на элементы станка (связи), удерживающие заготовку при обработке. Кроме того, по выбранным направлениям удобно измерять силы в экспериментах по резанию.

Касательную силу Р называют силой резания. Она всегда направлена по абсолютной траектории резания в сторону движения резца. Нормальная сила может проявляться как сила отжима Q (резец отжимает заготовку от заданной поверхности резания в сторону массива древесины) при Q_л+Q₃>Q_п или как сила затягиванияQ | (резец затягивает заготовку в сторону срезаемой стружки) при Q_л+Q₃ | ) пользуются для удобства.

В процессе резания резец взаимодействует с древесиной. При этом одновременно действуют рассмотренные силы воздействия резца на древесину и противоположно направленные, равные им по величине силы воздействия древесины на резец.

При силовых и мощностных расчетах режимов резания пользуются следующими основными понятиями и соотношениями.

Обычно вычисляют единичную силу резания Р₁(Н/мм) – силу резания, приходящуюся на единицу ширины срезаемого слоя. Считают, что полная сила резания Р всегда пропорциональна ширине срезаемого слоя В(мм): Р=Р₁В.

Удельной силой резания К, понятие которой ввел И.А.Тиме, называется сила резания, приходящаяся на единицу площади поперечного сечения стружки:

При расчете мощности, затрачиваемой на резание, используют понятие удельной работы резания К (Дж/см 3 ), под которой понимают работу А(Дж) силы резания Р(Н) на пути L(м), отнесенную к величине номинального объема V_H(см 3 ) срезаемого слоя: К=А/V_H=РL/(ВhL). Отсюда следует, что удельная работа К при выбранных размерностях численно равна удельной силе К (в последней формуле L сокращается), поэтому их обозначают одной буквой и в справочниках для них приводят общие таблицы. С физической точки зрения это разные величины с разной размерностью.

Из последней формулы следует, что А=КV_H. Мощность резания N_рез (Вт) – это работа в единицу времени (1с): N_рез=А/t=КV_H/t=КV_H1, где V_H1=V/t – номинальный объем стружки, срезанной за 1с (см 3 /с).

Когда известна сила резания Р(Н), мощность резания вычисляют по известной формуле механики N_рез=РV(пренебрегая различием в величине и направлении V_а и V).

В общем случае удельная сила и удельная работа резания К не являются величинами постоянными: они зависят от многих факторов процесса резания, но главным образом, от толщины срезаемого слоя и направления вектора скорости относительно волокон.

Теоретически определить К сложно, поэтому на практике используют средние значения этой величины, полученные экспериментально.

Стружкообразование

Форма стружки связана с усилением резания и качеством обработанной поверхности. Теория стружкообразования, изучающая закономерности образования стружки, даст возможность управлять процессом резания. Общая схема стружкообразования близка к случаю резания поперек волокон при условии, что в этом направлении древесина подобна пзотропному материалу со свойствами, средними между ранней и поздней древесиной. Резец идеально острый (Q=0), поэтому S_л= S_з = 0 и S=S_п.

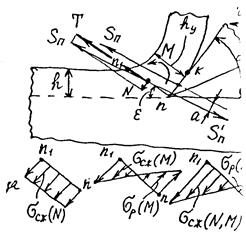
При внедрении в древесину резец деформирует подрезанную лезвием стружку. Стружка соприкасается с передней гранью на участке nh, а выше отходит от нее, закручивается из-за неодинаковой деформации наружных и внутренних слоев. Граница между срезанной и несрезанной частями стружки проходит через лезвие n и точку n₁, где изгибается верхняя поверхность стружки. Считают, что стружка образуется по плоскости nn₁, положение которой определяется углом наклона E к поверхности резания. Перенесем S_п в середину nn₁ (новое начало координат). В этой точке приложим две равные по величине S_п силы, одна из которых сонаправлена S_п, а другая S`<sub>п</sub> ей противонаправлена. Со стороны подрезанной стружки на неподрезанную в плоскости nn1 действуют сила S<sub>п</sub> и момент М=S<sub>п</sub> а, где а – плечо пары сил S<sub>п</sub> и S`_п. Разложим S_п на составляющие Т (по плоскости nn₁) и N (по нормали к nn₁). Т вызывает сдвиг подрезанной стружки вдоль nn₁, создавая касательные напряжения tпо этому сечению. N прижимает стружки к nn₁, вызывая нормальные напряжения сжатия d_сж(N) по nn₁. Изгибающий момент М создает нормальные напряжения сжатия d_сж(М) в верхней зоне стружки и растяжения d_р (М) в нижней. Касательные напряжения Н распределены по плоскости nn₁ почти равномерно. d(N,M) в n (у лезвия) растягивающие, т.к. обычно d_р(М)>> d_сж(N). В точке n₁ t (N,M) всегда напряжение сжатия.

Напряжения t,d_сж, d_р в плоскости стружкообразования nn₁ зависят главным образом от свойств древесины, толщины h стружки, угла резания d, радиуса затупления Q и коэффициента трения f_п.

Чем глубже внедряется резец в древесину, тем больше напряжение в стружке (при углублении резца). Нарастают они неравномерно и в зависимости от условий резания, одно из них раньше других достигает предела упругости или предела прочности. Это напряжение будет определять вид разрушения стружки, ее форму, качество обработанной поверхности. По основным структурным направлениям древесина по разному сопротивляется различным видам напряжений, что объясняет выше сказанное многообразие форм стружки.

Стружкообразование при резании поперек волокон.В направлении поперек волокон древесина хуже всего сопротивляется растяжению, лучше – сдвигу (скалыванию) и еще лучше – сжатию. Вид стружкообразования определяет касательное напряжение сдвига tв плоскости nn₁ или d_р в точке n.

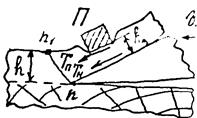
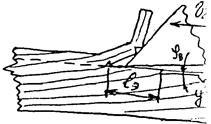
При определяющей роли t стружка может быть сливной (лента или спираль без внутренних трещин) или элементной (из элементов)

В первом случае t

Источник

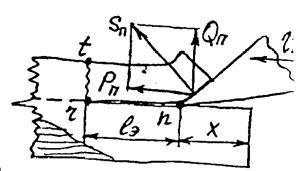
Удельная работа, затраченная на разрыв – а.

Предел пропорциональностиσ_пц — наибольшее напряжение, до которого справедлив закон Гука, (МПа):

Предел упругости σ_у — напряжение, после которого появляется остаточное удлинение.В тех случаях, когда не требуется высокой точности, предел упругости принимается равным пределу про­порциональности.

За­тем криволинейная часть диаграммы переходит в почти горизон­тальный участок — площадку текучести. Здесь деформации рас­тут практически без увеличения нагрузки (участок ВС).

Эти линии представляет собой следы смещения отдельных частиц материала, обусловленного большими деформациями образца. Они называются линиями Чернова

Предел текучестиσ_т — наименьшее напряжение, при котором образец деформируется без увеличения нагрузки (МПа):

Временное сопротивление σ_вявляется основным показателем прочности материала и представляет собой наибольшее напряже­ние, которое выдерживает материал перед разрушением (МПа):

Относительное удлинение ε — отношение абсолютного удлине­ния к первоначальной длине, выраженное в процентах:

(6)

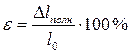
Относительное сужениеψ— отношение уменьшения площади поперечного сечения образца после разрушения к первоначальной площади поперечного сечения, выраженное в процентах:

17. Основные механические характеристики материалов. Пластичные и хрупкие материалы. Явление наклепа.

Понятия предел прочности и временное сопротивление разрыву не являются тождественными. Предел прочности относится к случаю, когда образец разрушается без образования шейки, что характерно для хрупких материалов. Временное сопротивление разрыву относится к пластичным материалам.

Наклеп – изменение структуры и свойств металлического материала, вызванное пластической деформацией. Наклеп снижает пластичность и ударную вязкость, но увеличивает предел пропорциональность, предел текучести и твердость. Наклеп снижает сопротивление материала деформации противоположного знака. При поверхностном наклепе изменяется остаточное напряженное состояние в материале и повышается его усталостная прочность. Наклеп возникает при обработке металлов давлением (прокатка, волочение, ковка, штамповка), резанием, при обкатке роликами, при специальной обработке дробью.

Повышение долговечности деталей машин методом поверхностного пластического деформирования (ППД) или поверхностного наклепа широко используется в промышленности для повышения

сопротивляемости малоцикловой и многоцикловой усталости деталей машин. На рисунке 3 приведены схемы различных ППД.

18. Анализ диаграммы растяжения. Определение полной работы.

Прямолинейный участок диаграммы продолжается до некоторой точки А, за которой прекращается действие закона Гука. Нагруз­ка F_пц, соответствующая точке А, служит для вычисления предела пропорциональности. Точка А (рис. 3) соответствует напряжению предела пропорци­ональности σ_пц.

Предел пропорциональностиσ_пц — наибольшее напряжение, до которого справедлив закон Гука, (МПа):

(1)

Площадь поперечного сечения образца на участке ОА практичес­ки не изменяется. Отсюда зона ОА именуется зоной упругости материала.

Предел упругости σ_у — напряжение, после которого появляется остаточное удлинение.В тех случаях, когда не требуется высокой точности, предел упругости принимается равным пределу про­порциональности. За­тем криволинейная часть диаграммы переходит в почти горизон­тальный участок — площадку текучести. Здесь деформации рас­тут практически без увеличения нагрузки (участок ВС). Точка С соответствует пределу текучестиσ_т.

Предел текучестиσ_т — наименьшее напряжение, при котором образец деформируется без увеличения нагрузки (МПа):

(2)

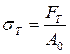
Зона ВС называется зоной общей текучести. На участке текучести ВС происходит существенная пластичес­кая деформация

Временное сопротивление σ_вявляется основным показателем прочности материала и представляет собой наибольшее напряже­ние, которое выдерживает материал перед разрушением (МПа):

(3)

Зона CD называется зоной распределения. точка D на диаграмме соответствует напряжению предела прочности — временного сопротивленияσ_в).

По диаграмме растяжения можно подсчитать работу, затрачен­ную на разрыв образца. Она выражается площадью диаграммы, за­ключенной между кривой деформирования ОАВСDК (рис. 3) и осью абсцисс. Чем больше работа, затраченная на разрыв образ­ца, тем больше энергии может поглотить образец без разрушения и тем лучше он будет сопротивляться ударным нагрузкам. Для по­лучения величины, характеризующей не образец, а его материал, подсчитывается удельная работа разрыва а , т.е. количество работы, приходящееся на единицу объема образца:

19. Определение коэффи­циента Пуассона и модуля продольной упругости. Метод электротензометрирования. Диаграмма напряжений.

Определение коэффициента Пуас­сонаμ. Коэффициентом поперечной деформации или коэффициентом Пуассона называется отношение относительной поперечной деформации образца при растяжении (сжатии) ε‘ к отно­сительной продольной деформации ε,найденных в пределах пропорциональности:

(3)

Это отношение для каждого материала, в пределах упругости явля­ется величиной постоянной – упругой константой.

Для определения коэффициента поперечной деформации необхо­димо подвергнуть образец растяжению (или сжатию) в пределах пропорциональности, с измерениями продольных и поперечных его деформаций.

Испытание производится на образце прямоугольного поперечно­го сечения, который описан и использован при опытном определе­нии модуля упругости Е. Там же указывалась методика нахождения продольных деформаций такого образца. Для измере­ния поперечных деформаций при нагружении образца в соответствую­щем его направлении наклеиваются тензорезисторы. Их необходимо также располагать попарно на противоположных плоскостях образ­ца (рис. 4) с целью устранения влияния возможного малого его искривления и возможной внецентренности приложения нагруз­ки. При такой установке тензорезисторов можно, найдя попереч­ные деформации образца на противоположных плоскостях, привести их к деформации его по средней плоскости, взяв среднее арифме­тическое соответствующих деформаций, т.е.

где ε’₂, ε’₃ – относительные поперечные деформации на противопо­ложных плоскостях образца, полученные по показа­ниям тензорезисторов Т2 и ТЗ (рис. 4);

ε’ – относительная поперечная деформация в средней плос­кости испытываемого образца.

По усредненному значению продольных ε_сри поперечных ε’_срдеформаций, соответствующих интервалу нагружения образца, подсчитывается коэффициент Пуассона (3):

20. Геометрические характеристики плоских сечений. Статический момент. Определение центра тяжести плоской фигуры.

При расчетах элементов конструкций используются различные геометрические характеристики, а именно:

1) Площадь поперечного сечения (см2, мм2).

2) Статические моменты сечения (см3, мм3).

3) Осевые моменты инерции сечения (см4, мм4).

4) Полярные моменты инерции сечения (см4, мм4).

5) Центробежные моменты инерции (см4, мм4).

6) Осевые и полярные моменты сопротивления сечения (см3, мм3).

Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):

Источник