Как показать что отрезки пересекаются

Отрезок. Ломаная линия

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Рис. 2 Несколько отрезков на прямой

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

Рис. 4 Отрезок без прямой

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

Рис. 7 Построение произвольного отрезка

Измерить отрезок можно:

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

На рисунке 12 видно, что:

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Урок 32. Пересекаются ли два отрезка?

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель. Напишем еще три новые функции.

Функция LinesCross() будет определять, пересекаются ли два отрезка. В ней взаимное расположение отрезков определяется с помощью векторных произведений. Для вычисления векторных произведений напишем функцию — VektorMulti().

Функция RealLess() будет использоваться для реализации операции сравнения «

Задача1. Два отрезка заданы своими координатами. Составить программу, которая определяет, пересекаются ли эти отрезки, не находя точку пересечения.

Решение
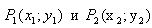
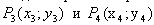
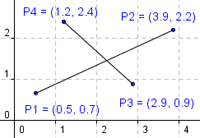
Пусть даны два отрезка. Первый задан точками . Второй задан точками .

Взаимное расположение отрезков можно проверить с помощью векторных произведений:

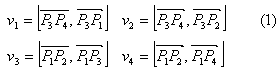
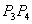
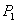
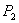
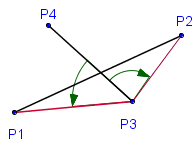
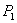
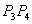
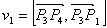
Рассмотрим отрезок и точки и .

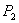
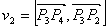
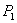
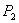
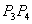
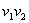
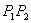
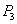
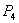
Точка лежит слева от прямой , для нее векторное произведение > 0, так как векторы положительно ориентированы.

Точка расположена справа от прямой, для нее векторное произведение и , лежали по разные стороны от прямой , достаточно, чтобы выполнялось условие и точек и .

Итак, если 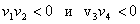, то отрезки пересекаются.

Для проверки этого условия используется функцию LinesCross(), а для вычисления векторных произведений – функция VektorMulti().

Векторное произведение двух векторов вычисляется по формуле:

ax, ay — координаты первого вектора,

bx, by — координаты второго вектора.

Результаты выполнения программы:

Мы написали программу, определяющую, пересекаются ли отрезки, заданные своими координатами.

На следующем уроке мы составим алгоритм, с помощью которого можно будет определить, лежит ли точка внутри треугольника.

Уважаемый читатель. Вы уже познакомились с несколькими уроками из серии «Геометрические алгоритмы». Все ли доступно написано? Я буду Вам очень признательна, если Вы оставите отзыв об этих уроках. Возможно, что-то нужно еще доработать.

Источник

Нахождение точки пересечения двух прямых (и отрезков)

Введение

Довольно часто при разработке игр возникает необходимость находить точку пересечения прямых, отрезков, лучей и т.д. О том, как реализовать это максимально простым способом, в этой статье.

Популярные способы и их критика

Возможно, многие вспомнят способ из школьной алгебры — составить уравнения двух прямых, приравнять их правые части, найти x, и подставить его в уравнение прямой, чтобы найти y (Подробнее здесь).

Однако данный способ становится достаточно громоздким при написании кода (возможно поэтому вы сейчас читаете эту статью), к тому же, он не является универсальным: если одна из прямых параллельна оси Y, мы получим ошибку деления на ноль при вычислении углового коэффициента, и нам придётся прописать код на этот случай; если две прямые перпендикулярны осям, требуется повозиться с обработкой и этого случая. Такой код становится длинным и некрасивым.

В поисках более элегантного решения данной проблемы я наткнулся на весьма интересные способы, основанные на векторном умножении ( habr.com/ru/post/267037 ) и ray castinging’е ( ru.wikipedia.org/wiki/Ray_casting#Концепция ). Но на мой взгляд, они неоправданно сложные в вычислительном плане. Поэтому представляю вашему вниманию (и критике) мой способ.

Мой способ

Задача

Даны координаты двух отрезков. Нужно узнать, пересекаются ли отрезки, и если да, в какой точке. Для этой цели напишем функцию.

Решение

Условные обозначения для исключения недопониманий: a — вектор a, a(y) — проекция вектора a на ось Y, a — вектор a, заданный координатами x1,y1.

Представим наши отрезки в виде двух векторов: a и b. Обратите, внимание, что вектор b имеет противоположное от ожидаемого направление. Введём вектор c. Заметим, что a*k+b*n=c, где k,n — некоторые коэффициенты. Таким образом, получаем систему уравнений:

a(x)*k+b(x)*n=c(x)
a(y)*k+b(y)*n=c(y)
Наша задача сводится к нахождению этих коэффициентов (правда сказать, достаточно найти лишь один из них).

Внимательный читатель заметит, что при a(y)=0, мы получим ошибку. Пропишем ветвление на этапе нахождения a(y). Этот случай ещё проще, ведь мы сразу получаем уравнение с одной неизвестной.

Рекомендую попробовать вывести n самостоятельно, так будет понятнее, что откуда берётся в коде ниже.

Зная n, можно найти точку пересечения, для этого мы отнимем от координаты точки (x3,y3) вектор b*n

Собираем воедино

Данная функция принимает координаты вершин и возвращает значение 1, если прямые отрезков (именно прямые) пересекаются, иначе 0. Если же вам нужны координаты вершин, вы сможете взять их из массива dot[].

Важно: при введении двух совпадающих прямых, алгоритм выводит отсутствие пересечения. Алгоритм находит точку пересечения прямых, на которых лежат отрезки, поэтому точка может оказаться за пределами отрезка (что вам придётся дополнительно проверить в уже своём коде).

Источник

Пересечение прямых, угол и координаты пересечения

IP76 > Пересечение прямых, угол и координаты пересечения

Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x₁-x₂) никак не разделить и т.д.

Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.

Коэффициенты А, B, C

Все помним со школы формулу:

Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):

Те же фаберже, только сбоку.

В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.

Загвоздка в том, что мы не знаем коэффициенты для обеих линий.

В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:

Путем несложных операций приходим к следующей записи:

Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:

Пока все идет отлично, нигде вероятного деления на ноль не встретилось.

Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.

Система уравнений

Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.

Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.

Сразу же запишем метод под нашу систему.

Имеем следующую систему:

Исходя из метода, решение выглядит так:

Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности). В коде, естественно, этот момент надо учитывать.

Практика 1

Частные случаи

Принадлежность точки отрезку

В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:

Займемся пунктом 2. Данный факт можно установить двумя способами:

Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.

Угол пересечения прямых

Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p₁ и p₂, получим направляющий вектор V(p₁,p₂), и аналогично второй вектор M(p₃,p₄). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.

Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:

Рис.4. Вектор V(p₁,p₂)

α — угол наклона вектора к оси X, который можно найти, как:

Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…

Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.

Рис.5. Пересекающиеся вектор V(p₁,p₂) и вектор M(p₃,p₄)

Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.

Рис.6. Пересекающиеся векторы в положительной Y

По рисунку явно видно, что угол между векторам это γ = (β — α).

В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.

От теории к практике

Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.

Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.

Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:

Источник