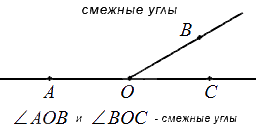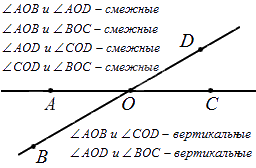Как показать что углы равны
Геометрия. Урок 2. Углы
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Понятие угла
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
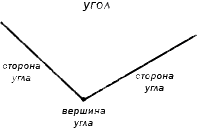
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.
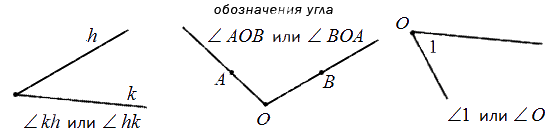
Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Виды углов:
Биссектриса угла
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
∠ A O D = ∠ B O D = ∠ A O B 2
Углы, образованные при пересечении двух прямых
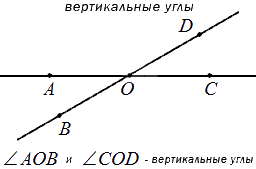
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
По свойству вертикальных углов:
∠ C O D = ∠ A O B
∠ B O D = ∠ A O C
( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )
По свойству смежных углов:
∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °
Углы, образованные при пересечении двух прямых секущей
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )
Сумма углов многоугольника
Сумма углов произвольного n -угольника вычисляется по формуле:
Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °
Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °
Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
α n = 180 ° ⋅ ( n − 2 ) n
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с углами
Как показать что углы равны
Угол — это геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла). Плоскость, содержащая обе стороны угла, делится углом на две области.
Содержание:
На рисунке 2.47 изображена прямая 
, на ней отмечена точка В, которая разделяет прямую 
на три части:
1) первая состоит из точек, лежащих левее точки В;
2) вторая состоит из самой точки В;
3) третья состоит из точек, лежащих правее точки В.
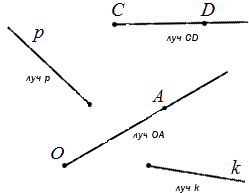
Объединение первого или третьего множеств с точкой В называется лучом или полупрямой. Таким образом, точка В определила на прямой 
два луча.
Точка В называется началом каждого из этих лучей или начальной точкой полупрямой.
Луч обозначается латинскими буквами: одной строчной (например, 
на рис. 2.48) или двумя заглавными, одна из которых обозначает начало луча, а вторая — какую-либо точку на луче (например, луч ВС на рис. 2.49).
Полупрямые прямой , на которые она разбивается точкой В, называются дополнительными.
В повседневной жизни мы часто употребляем понятие направления: направление движения пешехода или автомобиля, направление удара мяча в
футбольном матче, направление полета самолета или ракеты и т. д.
При задании направления используют понятие луча. В геометрии считают, что направление задается лучом, а определить понятие «направление» можно как множество лучей, сонаправлен-ных (одинаково направленных) с данным (рис. 2.50).
1. Если два луча лежат на одной прямой, то будем считать их одинаково направленными, если один из них содержится в другом, и противоположно направленными, если один из них не содержится в другом.
2. Если два луча параллельны, но не лежат на одной прямой, то проведем через их начала плоскость, которая разделит пространство на два полупространства. Если лучи лежат в одном из этих полупространств, то они сонаправлены (рис. 2.51). Если же лучи лежат в разных полупространствах, то они противоположно направлены (рис. 2.52).
Понятие угла
На рисунке 2.53 два луча OA и ОВ имеют общее начало. Эти два луча с общим началом всегда лежат в одной плоскости.
При таком расположении лучи разбивают плоскость, которую они образуют, на две части (рис. 2.54). Эти части плоскости вместе с образовавшими их лучами в геометрии называются углами.
Определение. Углом называется фигура, состоящая из двух различных лучей с общим началом и ограниченной ими части плоскости.
На рисунке 2.54 лучи OA и ОВ имеют общее начало — точку О и разбивают плоскость на две части. Исходя из определения угла, получили два различных угла.
Точка, из которой выходят ограничивающие угол лучи, называется вершиной угла, а сами лучи — сторонами угла (рис. 2.55). Лучи OA и ОС на этом рисунке определяют два угла.
Весь угол изобразить на рисунке нельзя, как нельзя на рисунке изобразить весь луч. Каждый угол в действительности продолжается бесконечно. На рисунке 2.56 выделены только части изображенных углов.
Слово «угол» иногда заменяют знаком 
. Часто при изображении угла чертят только выходящие из вершины начальные участки его сторон, а ту часть, которую хотят указать, обозначают дужкой (рис. 2.57)
Угол обозначается или одной заглавной буквой, поставленной у вершины угла, например: 
(рис. 2.57), или тремя буквами, из которых одна ставится при вершине угла, а две другие — у каких-нибудь точек сторон, например: 
(рис. 2.57). Буква, стоящая при вершине угла, всегда записывается между двумя другими буквами. Иногда угол обозначают цифрой, поставленной внутри угла (рис. 2.58).
Для изучения свойств углов используется понятие луча, проходящего между сторонами угла.
Определение. Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
На рисунке 2.59 луч ОВ проходит между сторонами угла АОС, так как он исходит из вершины угла АОС и пересекает отрезок MP. Концы отрезка MP лежат на сторонах угла АОС.
Возьмем луч АС (рис. 2.60) и будем поворачивать его вокруг точки А против часовой стрелки, например, до положения АВ, тогда его последовательные положения «заметут» угол со сторонами АС и АВ.
Продолжая вращать луч в том же направлении, мы будем получать все новые и новые углы. В определенный момент оба луча составят прямую линию (рис. 2.61). Такой угол называется развернутым углом.
Развернутый угол есть часть плоскости, ограниченная прямой, т. е. полуплоскость (рис. 2.62). Сторонами развернутого угла являются две дополнительные полупрямые.
Определение. Развернутым углом называют угол, стороны которого являются дополнительными полупрямыми одной прямой.
Если продолжить вращение луча дальше, чем показано на рисунке 2.62, то будут получаться новые углы (рис. 2.63), пока луч не вернется в свое первоначальное положение (рис. 2.64).
Самый большой возможный угол, полученный в ходе вращения луча, называется полным углом. Полный угол, в сущности, есть вся плоскость (рис. 2.65), а не ее часть, ограниченная двумя лучами.
Измерение углов
Каждый угол характеризуется его величиной, которая называется градусной мерой угла. Измерение углов осуществляется аналогично измерению отрезков — оно основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус — угол, равный 
части развернутого угла. Градус обозначают знаком 
.
Градусную меру часто называют просто величиной угла. Величина угла, равного 
части градуса, называется минутой и обозначается знаком 
, часть минуты называется секундой и обозначается знаком 
. Например, угол в 60 градусов 32 минуты 17 секунд записывается так: 60°32’17».
Так как градус составляет часть развернутого угла, развернутый угол равен 180°.
Определение. Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называют градусной мерой угла.
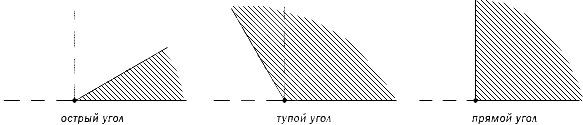
В зависимости от градусной меры углы бывают трех видов: острые, прямые и тупые.
Определение. Угол, равный 90°, называют прямым углом. Прямой угол обозначается буквой d. Угол, меньший 90°, называют острым углом. Угол, больший 90°, называют тупым углом.
Градусные меры угла обозначаются или так же, как сами углы, или буквами греческого алфавита. Например, запись 
читается: величина (или градусная мера) угла АОВ равна 45 градусам. На рисунке 2.66 величина острого угла записана: 
, читаем: величина угла 
меньше 90 градусов. Аналогично записываются и читаются величины прямого и тупого углов (рис. 2.67, 2.68).
Основные свойства измерения углов
Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Например, на рисунке 2.69 луч ОС проходит между сторонами угла АОВ, градусная мера угла АОВ равна сумме градусных мер углов АОС и СОВ, то есть 
Для измерения градусных мер углов (величин углов) на уроках геометрии применяется транспортир (рис. 2.70). На рисунке 2.71 показано, как с помощью транспортира можно измерять угол в 30°, 90°, 120°. На рисунке 2.72 показано, как с помощью транспортира можно отложить от полупрямой OA в верхнюю полуплоскость угол с данной градусной мерой 60°.
Пример:
Между сторонами угла COD, равного 120°, проходит луч OA. Найдите углы СОА и AOD, если их градусные меры относятся как 4:2.
Решение:
Из условия задачи имеем:
1. 
2. Луч OA проходит между сторонами угла COD.
3. 
Найдите градусные меры углов СОА и AOD.
4. 
(2, свойства измерения углов).
5. Так как градусные меры углов СОА и AOD относятся как 4:2, то можно считать, что 
состоит из 6 частей (1, 2, 3, 4).
6. 
Равенство углов. Биссектриса угла
Как и при определении равенства отрезков, рассматриваются два определения равенства углов.
Определение. Углы равны, если равны их градусные меры.
На рисунке 2.73 изображены два угла ABC и DEM, величины которых равны, а значит, по определению, эти углы равны. Равенство углов обозначается так: 
Определение. Углы называются равными, если их можно совместить наложением друг на друга.
Развернутые углы при наложении всегда могут быть совмещены. Отсюда следует, что все развернутые углы равны между собой. Полные углы равны между собой.
Пусть есть два угла: 
(рис. 2.74). Если угол 1 наложить на угол 2 так, чтобы их вершины совпали, одна из сторон угла 1 совместится со стороной угла 2, но при этом угол 1 составит только часть угла 2 (рис. 2.75). В этом случае говорят, что величина угла 1 меньше величины угла 2. Можно сформулировать по-другому: угол 1 меньше угла 2.
Используя понятие равенства углов, можно дать определение одному из важных понятий геометрии — биссектрисе угла.
Определение. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
На рисунке 2.76 луч ОМ — биссектриса угла АОВ, при этом 
Смежные углы
Определение. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 2.77 
являются смежными, так как лучи OA и ОС — дополнительные полупрямые, а луч ОВ — общая сторона этих углов.
Теорема 4.
Сумма смежных углов равна 180°.
Из теоремы 4 вытекают следующие следствия — свойства смежных углов.
Следствие 1. Если два угла равны, то смежные с ними углы равны.
Следствие 2. Угол, смежный с прямым углом, есть прямой угол.
Следствие 3. Угол, смежный с острым, является тупым, а смежный с тупым — острым.
Вертикальные углы
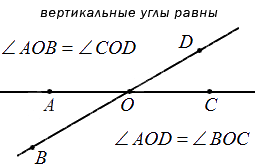
На рисунке 2.78 изображены две пересекающиеся в точке О прямые АВ и CD. При пересечении этих прямых образовалось четыре угла: 
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
На рисунке 2.78 углы 1 и 3, 2 и 4 вертикальные.
Теорема 5.
Вертикальные углы равны.
Очевидно, что две пересекающиеся прямые образуют смежные и вертикальные углы. Смежные углы дополняют друг друга до 180°. Угловая мера меньшего из них называется углом между прямыми.
Пример:
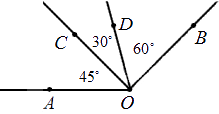
На рисунке 2.79 угол COD равен 30°. Чему равны углы АОК и DOK?
Решение:
Из условия задачи имеем:
1. Прямые СК и AD пересекаются в точке О.
2. 
(рис. 2.79)
3. Найдите углы АОК и DOK.
4. Углы COD и АОК вертикальные (1, определение вертикальных углов).
5. 
(2, свойство вертикальных углов).
6. Угол DOK смежный с углом COD (1, определение смежных углов).
7. 
(6, свойство смежных углов).
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
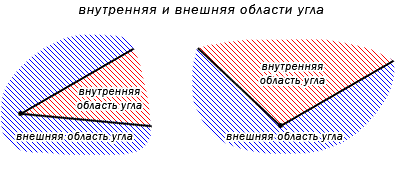
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
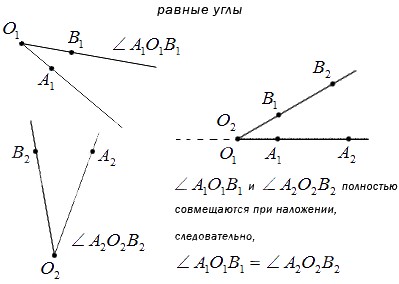
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
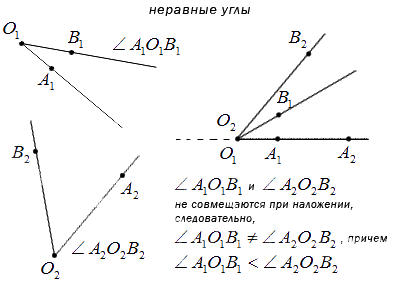
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « » ». Имеет место обозначение:
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
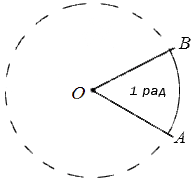
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
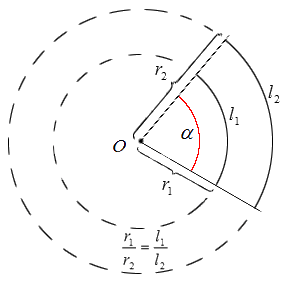
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
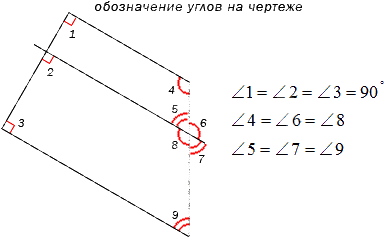
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
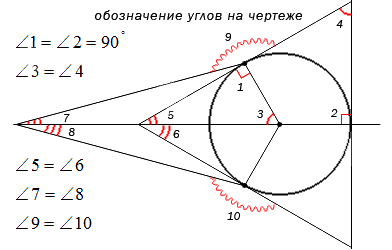
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.