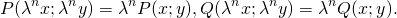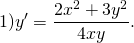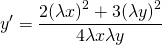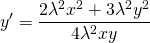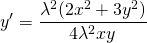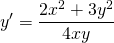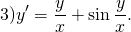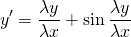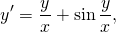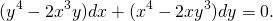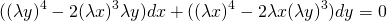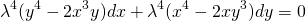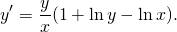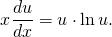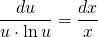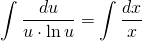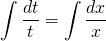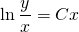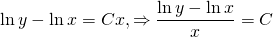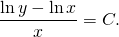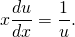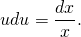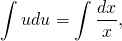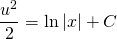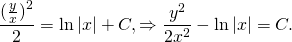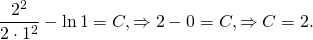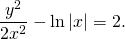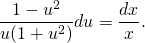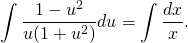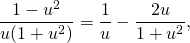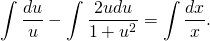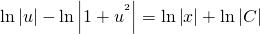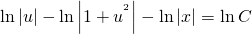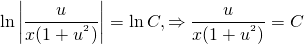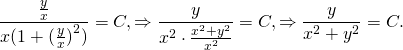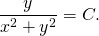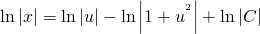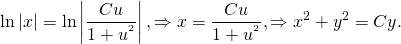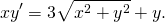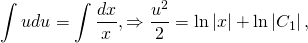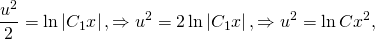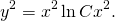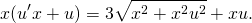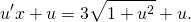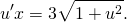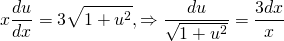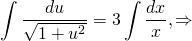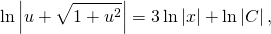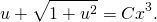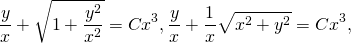Как понять что дифференциальное уравнение однородное
Как понять что дифференциальное уравнение однородное
Однородное дифференциальное уравнение можно решить с помощью подстановки \(y = ux,\) которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
Дифференциальное уравнение вида \[\left( <
Нетрудно заметить, что многочлены \(P\left(
Интегрируем последнее выражение: \[\int
Возвращаясь к старой переменной \(y,\) можно записать: \[y = ux = x\left( <2\ln \left| x \right| + C>\right).\] Таким образом, уравнение имеет два решения: \[y = x\left( <2\ln \left| x \right| + C>\right),\;\;x = 0.\]
Заметим, что корень \(x = 0\) не принадлежит области определения заданного дифференциального уравнения. Перепишем уравнение в следующей форме: \[y’ = \frac
Здесь мы снова встречаемся с однородным уравнением. В самом деле, запишем его в виде: \[
Как определить однородное уравнение
Дифференциальное уравнение 1-го порядка P(x;y)dx+Q(x;y)dy=0 называется однородным, если P(x;y) и Q(x;y) — однородные функции одинакового измерения, то есть
Как определить, что дифференциальное уравнение — однородное? На практике проверку уравнения на однородность проводят следующим образом: вместо каждого x подставляют λx, вместо каждого y — λy. При этом y’, dx и dy не трогают. После этого упрощают уравнение. Если после упрощения удается сократить на λ (или n- ю степень λ) и получить исходное уравнение, то это и означает, что данное уравнение является однородным уравнением 1-го порядка.
Другая форма записи: y’=f(x;y). Это уравнение является однородным, если функция f(x;y) является однородной функцией нулевого порядка. Это означает, что f(λx;λy)=f(x;y).
Подставляем вместо каждого x λx, вместо каждого y — λy:
Выносим лямбда в квадрате за скобки и сокращаем на него:
Пришли к исходному уравнению, а это значит, что данное уравнение — однородное.
2) (x-y)ydx-x²dy=0.
Подставляем вместо каждого x λx, вместо каждого y — λy: (λx-λy)λydx-(λx)²dy=0. Теперь выносим общий множитель λ² за скобки: λ²((x-y)ydx-x²dy)=0. Делим обе части уравнения на λ²:
(x-y)ydx-x²dy=0. Пришли к исходному уравнению, значит, это уравнение — однородное. (Здесь P(x;y) и Q(x;y) — однородные функции 2й степени).
Наличие дроби y/x уже косвенно указывает на то, что уравнение может быть однородным. Проверим, так ли это:
После сокращения на λ получаем исходное уравнение:
а это значит, что данное уравнение является однородным.
Подставляем вместо каждого x λx, вместо каждого y — λy:
Делим обе части уравнения на лямбда в 4й степени:
Получили исходное уравнение, а значит, оно является однородным. (Здесь P(x;y) и Q(x;y) — однородные функции 4й степени).
О дифференциальных уравнениях первого порядка
Что такое дифференциальные уравнения первого порядка
Обыкновенным дифференциальным уравнением называют такое уравнение, которое содержит функцию у(х) только от единственной переменной, к примеру, х.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Таким образом, в первой части можно наблюдать независимую переменную х, неизвестную функцию у(х) и производную данной функции y′(x). Во второй части заметна лишь вторая производная функции y″(x). Можно сделать вывод, что дифференциальным уравнение будет в том случае, когда имеется производная у(х) любого порядка.
Порядок дифференциального уравнения представляет собой порядок наибольшей производной неизвестной функции у(х) в выражении.
В первом варианте имеем наибольшую производную первого порядка. Из этого можно сделать вывод, что дифференциальное выражение также первого порядка. Во втором случае в уравнении имеется вторая производная y″(x), таким образом, данное дифференциальное уравнение второго порядка.
Общим решением дифференциального уравнения является комплекс функций y=f(x,C), подстановка которых в определенное выражение приводит к равенству обеих частей этого уравнения.
В данном выражении С является произвольной константой. Поиск подобных решений представляет собой интегрирование дифференциального уравнения.
Частным решением дифференциального уравнения называют такое решение, которое было получено в результате поиска константы С, согласно дополнительным условиям задачи.
Дифференциальные уравнения первого порядка делят на несколько основных видов, которые наиболее часто можно встретить при решении задач:
Алгоритм поиска решений дифференциальных уравнений:
Как определить однородное дифференциальное уравнение
Дифференциальное уравнение, которое относится к первому порядку, имеет вид:
Данное дифференциальное уравнение можно считать однородным в том случае, когда правая часть выражения соответствует условию:
В этом случае справедливы все значения t.
Таким образом, правая часть представляет собой однородную функцию нулевого порядка, относительно переменных x и y:
Другой вид записи однородного дифференциального уравнения:
Кроме того, уравнение можно представить с помощью дифференциалов:
\(P\left(
где \(P\left(
Функцию \(P\left(
Основным способом решения однородного дифференциального уравнения является подстановка y = ux, что позволяет преобразовать исходное выражение в уравнение, в котором присутствуют разделяющие переменные.
Таким образом, дифференциальное уравнение, записанное в виде:
\(\left( <
будет преобразовано в выражение, в котором имеются разделяющие переменные, путем перемещения начальной части координатной системы в точку пересечения прямых, заданных уравнением. В том случае, когда эти линии параллельны друг другу, дифференциальное уравнение можно свести к виду уравнения с разделяющими переменными с помощью подстановки переменной:
Метод решения однородного дифференциального уравнения
Проверка однородности предложенного уравнения выполняется путем замены x и y на λx и λy. Производная при этом остается неизменной. В том случае, когда все λ после преобразований будут удалены, можно сделать вывод о том, что искомое дифференциальное уравнение является дифференциальным уравнением первого порядка.
Решить дифференциальное уравнение первого порядка можно с помощью выполнения последовательных действий:
Примеры решения
Задача 1
Требуется найти решение дифференциального уравнения:
Решение
Заметим, что многочлены \(P\left(
Допустим, y = ux, где u – представляет собой какую-то новую функцию с зависимостью от х. В таком случае:
\(dy = d\left(
Полученное выражение можно подставить в дифференциальное уравнение:
\(\require
Можно поделить две части выражения на х, получим:
С помощью деления на x, можно было утратить решение x = 0. Благодаря прямой подстановке, удалось понять, что x = 0 действительно представляет собой одно из решений заданного уравнения.
Последнее выражение следует интегрировать:
В этом случае C является постоянной интегрирования.
Если вернуться к первоначальной переменной, то запись будет выглядеть следующим образом:
Получается, что у уравнения существует пара решений:
Задача 2
Необходимо найти решение для дифференциального уравнения:
\(xy’ = y\ln \large\frac
Решение
Можно заметить, что корень x = 0 не относится к области определения данного дифференциального уравнения. Следует представить выражение в таком виде:
Из чего становится понятно, что уравнение однородное.
Далее можно заменить y = ux. Таким образом:
Затем следует выполнить подстановку полученного выражения в первоначальное дифференциальное уравнение:
Если разделить две части уравнения на \(x \ne 0\) :
Таким образом, выражение будет записано в виде уравнения с разделяющимися переменными:
Следует проинтегрировать обе части равенства:
В результате получим:
Постоянная С в данном случае может быть записана, как:
В этом случае уравнение примет вид:
По итогам вычислений получаем пару решений:
В итоге, все решения дифференциального уравнения можно записать с помощью одного равенства:
где C является произвольным действительным числом.
Задача 3
Дано дифференциальное уравнение, решение которого требуется найти:
Решение
В данном примере также записано однородное дифференциальное уравнение. Выражение можно представить следующим образом:
Можно подставить y = ux. В таком случае, y’ = u’x + u. Подставляя y и y’ в исходное уравнение, получим:
Преобразованное уравнение будет записано в таком виде:
Найти общее решение можно путем интеграции:
следует записать последнее уравнение в виде:
Обратная функция \(x\left( y \right)\) будет записана в таком виде:
Исходя из того, что C является произвольным числом, знак «минус» перед этой константой можно заменить на знак «плюс». Путем преобразований получим:
\(x = y\ln \left| y \right| + Cy\)
В итоге представим запись дифференциального решения:
\(x = y\ln \left| y \right| + Cy,\;\;y = 0\)
Задача 4
Требуется решить дифференциальное уравнение, которое записано в виде:
Решение
Проанализировав правую часть уравнения, можно сделать вывод, что x \ne 0 и y \ne 0. Можно выполнить подстановку: y = ux, y’ = u’x + u. В итоге получим уравнение, в котором есть разделяющие переменные:
Далее следует интегрировать полученное выражение:
Заменим 2C на постоянную C. Получаем:
Общее решение дифференциального уравнения будет иметь вид:
Как решить однородное дифференциальное уравнение
Чтобы решить однородное дифференциальное уравнение 1-го порядка, используют подстановку u=y/x, то есть u — новая неизвестная функция, зависящая от икса. Отсюда y=ux. Производную y’ находим с помощью правила дифференцирования произведения: y’=(ux)’=u’x+x’u=u’x+u (так как x’=1). Для другой формы записи: dy=udx+xdu.После подстановки уравнение упрощаем и приходим к уравнению с разделяющимися переменными.
Примеры решения однородных дифференциальных уравнений 1-го порядка.
1) Решить уравнение
Проверяем, что это уравнение является однородным (см. Как определить однородное уравнение). Убедившись, делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем: u’x+u=u(1+ln(ux)-lnx). Так как логарифм произведения равен сумме логарифмов, ln(ux)=lnu+lnx. Отсюда
u’x+u=u(1+lnu+lnx-lnx). После приведения подобных слагаемых: u’x+u=u(1+lnu). Теперь раскрываем скобки
u’x+u=u+u·lnu. В обеих частях стоит u, отсюда u’x=u·lnu. Поскольку u — функция от икса, u’=du/dx. Подставляем,
Получили уравнение с разделяющимися переменными. Разделяем переменные, для чего обе части умножаем на dx и делим на x·u·lnu, при условии, что произведение x·u·lnu≠0
В левой части — табличный интеграл. В правой — делаем замену t=lnu, откуда dt=(lnu)’du=du/u
ln│t│=ln│x│+C. Но мы уже обсуждали, что в таких уравнениях вместо С удобнее взять ln│C│. Тогда
ln│t│=ln│x│+ln│C│. По свойству логарифмов: ln│t│=ln│Сx│. Отсюда t=Cx. ( по условию, x>0). Пора делать обратную замену: lnu=Cx. И еще одна обратная замена:
По свойству логарифмов:
Это — общий интеграл уравнения.
Вспоминаем условие произведение x·u·lnu≠0 (а значит, x≠0,u≠0, lnu≠0, откуда u≠1). Но x≠0 из условия, остается u≠1, откуда x≠y. Очевидно, что y=x ( x>0) входят в общее решение.
2) Найти частный интеграл уравнения y’=x/y+y/x, удовлетворяющий начальным условиям y(1)=2.
Сначала проверяем, что это уравнение является однородным (хотя наличие слагаемых y/x и x/y уже косвенно указывает на это). Затем делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем полученные выражения в уравнение:
u’x=1/u. Так как u — функция от икса, u’=du/dx:
Получили уравнение с разделяющимися переменными. Чтобы разделить переменные, умножаем обе части на dx и u и делим на x (x≠0 по условию, отсюда u≠0 тоже, значит, потери решений при этом не происходит).
и поскольку в обеих частях стоят табличные интегралы, сразу же получаем
Выполняем обратную замену:
Это — общий интеграл уравнения. Используем начальное условие y(1)=2, то есть подставляем в полученное решение y=2, x=1:
3) Найти общий интеграл однородного уравнения:
(x²-y²)dy-2xydx=0.
Замена u=y/x, откуда y=ux, dy=xdu+udx. Подставляем:
(x²-(ux)²)(xdu+udx)-2ux²dx=0. Выносим x² за скобки и делим на него обе части (при условии x≠0):
(1-u²)(xdu+udx)-2udx=0. Раскрываем скобки и упрощаем:
xdu-u²xdu-u³dx-udx=0. Группируем слагаемые с du и dx:
(x-u²x)du-(u³+u)dx=0. Выносим общие множители за скобки:
x(1-u²)du-u(u²+1)dx=0. Разделяем переменные:
x(1-u²)du=u(u²+1)dx. Для этого обе части уравнения делим на xu(u²+1)≠0 (соответственно, добавляем требования x≠0 (уже отметили), u≠0):
В правой части уравнения — табличный интеграл, рациональную дробь в левой части раскладываем на простые множители:
(или во втором интеграле можно было вместо подведения под знак дифференциала сделать замену t=1+u², dt=2udu — кому какой способ больше нравится). Получаем:
По свойствам логарифмов:
Вспоминаем условие u≠0. Отсюда y≠0. При С=0 y=0, значит, потери решений не происходит, и y=0 входит в общий интеграл.
Можно получить запись решения в другом виде, если слева оставить слагаемое с x:
Геометрический смысл интегральной кривой в этом случае — семейство окружностей с центрами на оси Oy и проходящих через начало координат.
Задания для самопроверки:
Так как u=y/x, u²=y²/x², то есть y²=u²x²,
2) Проверив, что данное уравнение является однородным, делаем замену y=ux, отсюда y’=u’x+u. Подставляем в условие:
Делим обе части уравнения на x:
Интегрируем обе части:
и, умножив на x обе части уравнения, получаем:\
Линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения 2-го порядка
Линейные однородные дифференциальные уравнения (ЛОДУ) 

Частным случаем дифференциальных уравнений (ДУ) такого типа называют линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.
Общее решение линейного однородного дифференциального уравнения 

Самое сложное заключается в определении линейно независимых частных решений ДУ такого типа. Зачастую, частные решения выбирают из таких систем линейно независимых функций:
Но достаточно редко частные решения представляются именно так.
Примером линейного однородного дифференциального уравнения можно назвать 
Общее решение линейного неоднородного дифференциального уравнения 

где y0 является общим решением соответствующего линейного однородного дифференциального уравнения,
а 

Как пример линейного неоднородного дифференциального уравнения приводим 
Познакомиться ближе с теорией и просмотреть примеры решений можете здесь: Линейные дифференциальные уравнения второго порядка.