Как понять что предел не существует

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

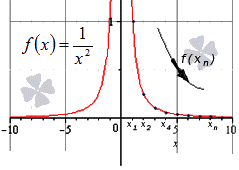
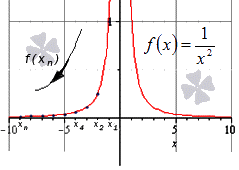
При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

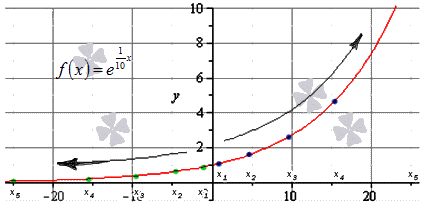
Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Пределы

Пределы — одни из самых трудных сущностей в математике для понимания. Сложно объяснить просто, что такое предел, поэтому чаще всего этого никто и не делает.

И тем более, мало к то из преподавателей может привести пример из жизни, когда пределы все-таки могут пригодиться. Но мы попытаемся объяснить так, чтобы было и понятно и несложно и по сути. Как обычно «на пальцах».

Что такое пределы простыми словами

Наверное самое наглядное, что можно вспомнить из истории, это знаменитый парадокс Зенона «Ахиллес и черепаха». Зенон был философом, а не математиком, поэтому мог вполне свободно упражняться в остроумии не заботясь о доказательствах.

Ахиллес и черепаха бегут на перегонки. Черепаха начинает первой, человек догоняет. Ахиллес бежит быстрее, но когда он пробегает 100 шагов, черепаха все рано проползает один. Еще 100 шагов и еще один. Таким образом Ахиллес приближается к черепахе но и она чуть-чуть отдаляется от него. Зенон делает вывод, что Ахиллес будет бесконечно к ней приближаться, но никогда не догонит черепаху!

В этой истории важно не то, что на самом деле она не реальна, а ее «математический смысл». Человек приближается к черепахе но никогда ее не настигает. То есть некий предел (черепаха) к которому стремится Ахиллес.

Говоря простым языком, предел это такое значение, которое нельзя достичь, но можно бесконечно близко к нему приблизится.

То есть, в пределе определенного промежутка времени Ахиллес действительно не догонит черепаху (времени не хватит), но приблизится к ней на бесконечно малое расстояние.

Что такое пределы в математике

Стоит сразу сказать, что определение пределов больше чем одно, потому, что они бывают разные. Есть придел последовательности, а есть предел функции.

Давайте разделим число 10 пополам:

10/2=5, и еще раз, 5/2=2,5 и еще…

Это последовательность n/2: 10…2,5…1,25…

Если делать это 20 раз получится вот такое значение: 0,000019

А если сделать 100 раз, то вот такое: 0,000000000000000000000000000016

Если делить пополам бесконечно, результат будет уменьшатся, в реальной жизни, это будет уже фактически ноль, но в математике, все еще не ноль… Предел этой последовательности будет стремиться к нолю.

Если взять другу последовательность, например n+1. 2…3…4…5… и снова устремимся в бесконечность. Предел этого множества тоже будет стремится к бесконечности.

Еще один пример

Бросаем монетку. Может выпасть «орел», а может и «решка». Теория вероятности утверждает, что шансы всегда 50/50, то есть вероятность «орла» — 1/2=0,5.

Каждый раз, значение реальной вероятности, приближается к расчетным 0,5. Чтобы получить вероятность ровно 0,5 нужно подбросить монетку бесконечное количество раз.

То есть, при условии, что количество бросков стремится к бесконечности предел предел будет равен 0,5.

Это именно та бесконечность из матанализа о которой было сказано в статьях об интегралах и делении на ноль. Это не какое-то определенное число — это понятие.

Предел последовательности

Предел последовательности — это пространство которое содержит все все элементы последовательности начиная с какого-то значения.

А простыми словами, предел последовательности, простыми словами, это такая «область» куда попадают все значения после определенного порога (в нашем случае – А). На изображении ниже она условно показана синей полоской.

ε — это произвольное положительное число.

Можно заметить, что при продолжении вверх последовательности ее значения все равно будут оставаться в пределах «синей полосы».

Можно сказать и так:

Предел числовой последовательности, это число (s на графике) в окрестности которого попадает бесконечно много значений. При этом вне предела, количество значений явно конечно.

Чтобы было еще понятнее: предел последовательности это значение (точка А) выше которого все будет попадать в область не больше s+ε и s-ε. Бесконечное количество таких значений будет «лежать» внутри синей полоски.

Математическим языком можно записать так: s-ε Предел функции простыми словами объяснить также просто. Предел в какой-то произвольной точке — это величина к которой значение функции приближается. Например, f(x)=2x, а х→0 (икс стремится к нулю).

В этом случае предел функции будет равен lim 2x=0. Или в случае если х→2 то предел равен lim 2x=4. Пока все просто. Вот только зачем вычислять пределы, если можно просто выбросить «lim» и расчеты останутся те ми же?….

Зачем нужны пределы

Пределы как раз и нужны тогда, когда мы имеем дело с бесконечностью. Например, бесконечно большими или бесконечно малыми значениями.

Непонятно, что такое «бесконечно большое» или «бесконечно долго», это не какое-то определенное число. С бесконечно малыми значениями та же ситуация, это не «ноль» но как-то очень близко к нему. Тут и выручают пределы.

В точке х=2 — пусто. Потому, что получается 0/0, то есть неопределенность. Но стоит вместо 2 подставить 1,9999999999(9) или 2,000000001(1). Значения бесконечно близкие к 2, но не «два», как график превратится в прямую.

В этом случае речь идет о пределе функции при «икс» стремящемуся к двум, функция стремится к 4.

Такой своеобразный «трюк» в расчетах с заменой знака равенства на стрелочку.

Нет, не совсем. Когда речь идет о пределах, имеется в виду процесс, не важно функция это или множество, но предел описывает процесс в динамике. Тогда как знак «равно» означает статическое состояние.

x=1 и x→1, это совсем не одно и то же.

Примеры из жизни

Зачем все это нужно где применяется пределы в реальных расчетах?

Простое объяснение пределов невозможно, если не привести наглядный пример. Но только где его взять? Существует ли какой-то физический смысл пределов? Не точный аналог но что-то похожее есть.

Можно провести простой эксперимент, взять, например, спичку. Или что-угодно, чего не жалко. Начинаем пытаться сломать спичку, сначала одно усилие, потом чуть больше и еще больше. В один из моментов спичка треснет пополам.

Поздравляем, вы достигли предела прочности. Можно повторить эксперимент с другими спичками и установить, значение при котором спичка ломается.

Что тут общего с пределами из математики, кроме названия.

Есть множество значений силы до предела прочности и оно ограничено, и множество значений после предела прочности, их неограниченное множество. Ведь спичка уже сломана, любое усилие выше предела прочности будет ломать новую и новую спичку. Точно так же как и с пределом функции или множества.

Все, что лежит за пределом, уже не имеет практического значения — спичка не устоит.

Еще один пример, это «практический потолок» летательного аппарата. Это максимальная высота на которую может «взобраться» самолет, чтобы подняться выше будет уже не хватать подъемной силы. Хотя на есть еще и понятие «динамический потолок» — это высота на которую можно подняться хорошенько разогнавшись.

Но, выскочив на эту высоту, через некоторое время самолет все равно опустится на свой «потолок».

Посмотрите на картинку ниже, это наглядный пример такого явления как резонанс.

Колебание моста из-за резонанса

Мост так раскачивается из-за того, что собственная частота колебания совпадает с той частотой с которой его раскачивает ветер, амплитуда колебаний постоянно возрастает и мост разрушается. В этом случае амплитуда стремится к бесконечности, так как в знаменателе формулы находится выражение w₀-w (собственная частота колебаний минус вынужденная частота), а так как обе w равны, получается то самое деление на ноль, а значит амплитуда → ∞.

Самое понятное объяснений пределов в реальности, с которым может столкнуться каждый — это сложные банковские проценты по кредиту. И если вы не умеете рассчитывать сложны проценты, не берите кредит. Для тех, кто силен в матанализе совет будет не лишним.

Также может понадобится рассчитать предельную стоимость товара, зная зависимость (функцию) цены от объема продаж или предельный объем производства или много еще чего.

Самый наглядный пример, возможно, это предел в маркетинге. Вот зависимость стоимости клика от количества кликов в контекстной рекламе.

И все же, в повседневной жизни обыватель редко встречается с таким понятием как предел функции или последовательности. Поэтому и так сложно понять и принять абстрактные математические формулировки.

Но, если постараться, математика может открыть новые грани реальности, по крайней мере, все это уже не будет казаться таким скучным и непонятным.

Источник

Как доказать что предела не существует

Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.

Постоянное число а называется пределом последовательности _n>, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x_n, у которых n>N, удовлетворяют неравенству

Последовательность, имеющая предел, называется сходящейся, в противном случае — расходящейся.

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x_n = f(n) целочисленного аргумента n.

Пусть дана функция f(x) и пусть a — предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности _n> значений аргумента, стремящейся к а, соответствующие им последовательности _n)> имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.

Определение 2. Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству
0 » 2.7 — основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а. Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x₀, если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x_o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x_o)= f(0) не определено, поэтому в точке x_o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x_o, если предел

и непрерывной слева в точке x_o, если предел

Непрерывность функции в точке x_o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x_o, например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x_o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x_o), то говорят, что функция f(x) в точке x_o имеет разрыв первого рода, или скачок.

Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода — в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3.1. Пользуясь определением предела числовой последовательности, доказать, что последовательность x_n =(n-1)/n имеет предел, равный 1.

Пример 3.2. Найти предел последовательности, заданной общим членом .

Пример 3.3. . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4. Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:

Пример 3.6. Доказать, что предел не существует.

Решение. Пусть x₁, x₂. x_n. — последовательность, для которой
. Как ведет себя последовательность _n)> = при различных x_n→ ∞

Если x_n= p n, то sin x_n= sin ( p n) = 0 при всех n и предел Если же
x_n=2 p n+ p /2, то sin x_n= sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Пример 3.7 Найти предел

Пример 3.8. Вычислить предел .

Решение. Обозначим y=π-x. Тогда при x→π, y→0. Имеем:

sin 3x = sin 3(π-y) = sin(3π-3y) = sin 3y.

sin 4x = sin 4(π-y) = sin (π4-4y)= — sin 4y.

_Предел

Пример 3.9. Найти предел .

Решение. Обозначим arcsin x=t. Тогда x=sin t и при x→0, t→0. .

Пример 3.10. Найти 1) ;

2) ;

3) .

1) Применяя теорему 1 предел разности и предел произведения, находим предел знаменателя: .

Предел знаменателя не равен нулю, поэтому, по теореме 1 предел частного, получаем:

.

2) Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ≠ 2 равенство:

Так как предел , то, по теореме предел частного, найдем

3. Числитель и знаменатель при x &rarr ∞ являются бесконечно большими функциями. Поэтому теорема предел частного непосредственно не применима. Разделим числитель и знаменатель на x 2 и к полученной функции применим теорему предел частного:

.

Пример 3.11. Найти предел .

Решение. Здесь числитель и знаменатель стремятся к нулю:, x-9→0, т.е. имеем неопределенность вида .

Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения , получим

.

Пример 3.12. Найти предел .

Решение.

Пример 3.6. Доказать, что предел lim sin(x) при x-> ∞ не существует.

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

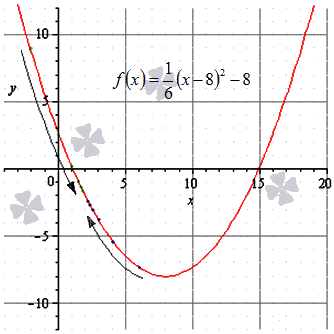
Докажите, что существует конечный предел функции f ( x ) = 1 6 ( x — 8 ) 2 — 8 в точке x 0 = 2 и вычислите его значение.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник