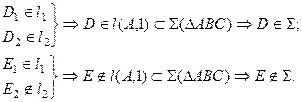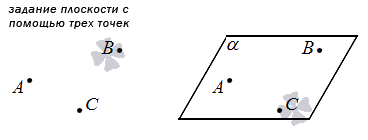Как понять что точки лежат в одной плоскости

Лежат ли точки в одной плоскости? Как это проверить?

Проверить, лежат ли в одной плоскости точки A,B,C,D
Проверить, лежат ли в одной плоскости точки A,B,C,D, и найти линейную зависимость векторов AB от AC.

Две точки на плоскости заданы своими координатами. Проверить, лежат ли они в одной координатной четверти
две точки на плоскости А(х1;у1) и В(х2;у2) задано своими координатами. Проверить, лежат ли эти.

Как пользуясь рангом матрицы определить лежат ли четыре точки трёхмерного пространства в одной плоскости
Как пользуясь рангом матрицы определить лежат ли четыре точки трёхмерного пространства в одной.

Лежат ли точки на одной плоскости
У тривимірному просторі задається n точок(3 9

Добавлено через 11 минут
Получится система уравнений:

Она вроде бы не совместна, направляющие вектора не параллельны, значит прямые не лежат в одной плоскости.

woldemas, вы пишете, что определитель из координат трех точек — это то же самое, что вычислить смешанное произведение векторов. Каких именно векторов? Ведь векторы в сообщении 2 строятся по четырем точкам. А три точки всегда лежат на одной плоскости.

Jessy James, чтобы определить, лежат ли четыре точки в трехмерном пространстве на одной плоскости, можно вычислить определитель 4×4, составленный из координат точек, к которым добавлена четвертая координата 1. Например, для точки A(1; 0; 2) используется строчка 1 0 2 1. Точки лежат на одной плоскости тогда и только тогда, когда определитель равено нулю.

Там одна из точек имеет нулевые координаты, если принять ее за начало для трех векторов проведенных к остальным точкам, можно просчитать определитель, в котором стоят координаты точек (но на самом деле это координаты радиус-векторов). Я думал это очевидно, поэтому и не стал особо расписывать.

Добавлено через 20 минут
А что касается условия принадлежности прямых одной плоскости, то определитель матрицы 3 на 3 составленной из направляющих векторов прямых и вектора соединяющего две любые точки на прямых должен равняться 0.

Лежат ли точки в одной плоскости?
На плоскости XOY даны три точки A(x1, y1), B(x2, y2), C(x3, y3). Выяснить, лежат ли они в одной и.

Лежат ли 4 точки в одной плоскости.
Помогите пожалуйста решить, лежат ли точки А(5,3,1), В(-3,2,3), С(3,8,6) и D(-3,1,2) в одной.

Определить, лежат ли три точки плоскости на одной прямой
Задача: Написать программу, определяющую, лежат ли три точки плоскости на одной прямой! Точки и.

Определить, лежат ли три точки плоскости на одной прямой
Помогите, пожалуйста с задачей! Написать программу, определяющую, лежат ли три точки плоскости на.

Источник

Как доказать что точка принадлежит плоскости

Для определения принадлежности точки и прямой плоскости, расположенной в пространстве, следует руководствоваться следующими ‘ положениями:

· точка принадлежит плоскости, если через нее можно провести линию, лежащую в плоскости;

· прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки;

· прямая принадлежит плоскости, если она проходит через точку данной плоскости параллельно прямой, принадлежащей этой плоскости.

Через одну точку на плоскости можно провести бесконечное множество линий. Это могут быть произвольные линии и линии, занимающие особое положение по отношению к плоскостям проекций П₁ П₂, П₃.Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно горизонтальной плоскости проекций, называется горизонталью плоскости.

Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно фронтальной плоскости проекций, называется фронталью плоскости.

Горизонталь и фронталь являются линиями уровня.

Горизонталь плоскости следует начинать строить с фронтальной проекции, т.к. она параллельна оси x, горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

А так как все горизонтали плоскости параллельны между собой, можно считать горизонтальный след плоскости нулевой горизонталью (рис. 5.8).

К линии уровня относится и профильная прямая, лежащая в заданной плоскости и параллельная П₃.

К главным линиям особого положения в плоскости, кроме линии уровня, относятся линии наибольшего наклонаплоскости к плоскости проекций.

Определение угла наклона плоскости

К плоскостям проекций

Плоскость общего положения, расположенная в пространстве
произвольно, наклонена к плоскостям проекций. Для определения величины двухгранного угла наклона заданной плоскости к какой-либо
плоскости проекции используются линии наибольшего наклона плоскости к плоскости проекций: к П₁ – линия ската, к П₂ – линия наибольшего наклона плоскости к плоскости П₂.

Линии наибольшего наклона плоскости – это прямые, образующие с плоскостью проекций наибольший угол, проводятся в плоскости перпендикулярно к соответствующей линии уровня. Линии наибольшего наклона и ее соответствующая проекция образуют линейный угол, которым измеряется величина двухгранного угла, составленное данной плоскостью и плоскостью проекций (рис. 5.10).

Последнее изменение этой страницы: 2016-12-10; Нарушение авторского права страницы

Рис. 3.2 Взаимное расположение прямых

Прямые в пространстве могут занимать относительно друг друга одно из трех положений:

1) быть параллельными;

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).

.

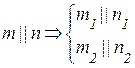
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

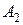
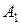
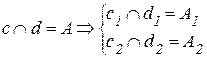
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная () и горизонтальная ()проекции этой точки должны находиться на одной линии связи.

.

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.

Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).

Признак принадлежности точки и прямой плоскости:

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

На рис. 3.5 изображена плоскость и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.

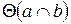
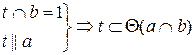
На рис. 3.6 показана плоскость и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.

.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 – | 7538 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

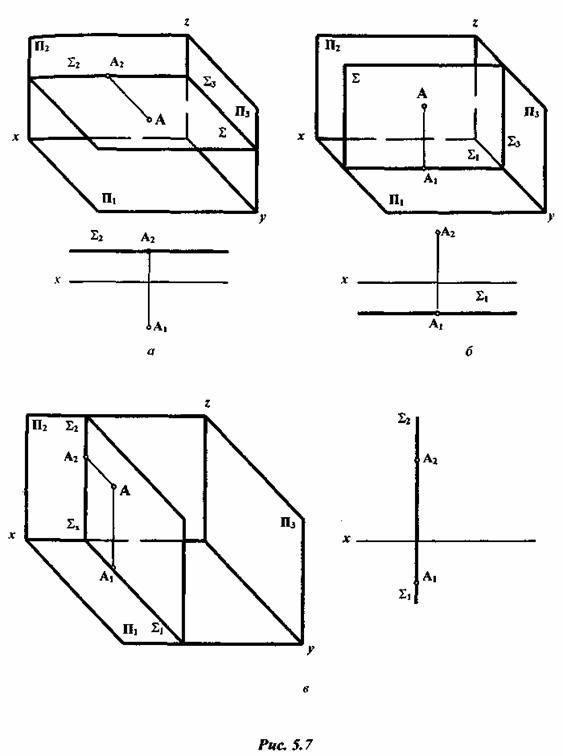
Принадлежность точки плоскости на комплексном чертеже определяется согласно аксиоме инцидентности или отношения принадлежности между элементами евклидова пространства, которая гласит: – если точка E принадлежит прямой k, а прямая k принадлежит плоскости α, то точка E принадлежит плоскости α: E ∈ k ∧ k ∈ α ⇒ E ∈ α.

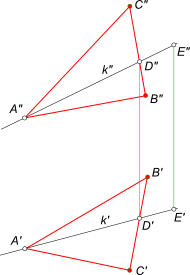
Задача на принадлежность точки плоскости может быть выражена следующим образом: – заключить точку E(E`, E») в; – провести через точку E(E`, E») плоскость α общего положения

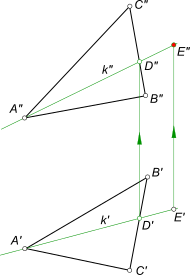
Положение плоскости α в пространстве определяется тремя точками – вершинами ΔABC. Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки A и D принадлежат этой плоскости. Проведя прямую в плоскости через точку E

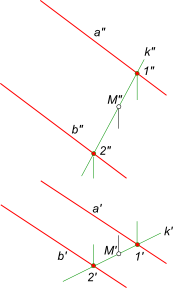
доказываем тем самым ее принадлежность заданной плоскости. Заключить точку M в плоскость α заданную параллельными прямыми a и b

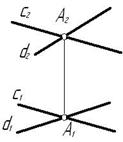
Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки 1 и 2 принадлежат этой плоскости. Построение искомой плоскости α: – проводим прямую через точку M; – через точки 1 и 2 взятые на прямой k проводим взаимно параллельные прямые a и b соответственно.

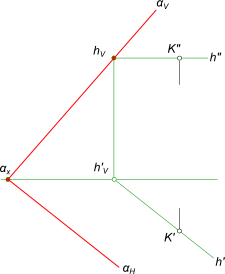
Через точку M провести плоскость α заданную следами

Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой h, которая, в то же время, принадлежит плоскости α и является ее горизонталью. Построение искомой плоскости α: – проводим прямую h (горизонталь искомой плоскости) через точку K; – проводим горизонтальный след α_H // h` ⇒ α_x; – через точки α_x и h_V проводим фронтальный след α_V.

Источник

Плоскость в пространстве – необходимые сведения

Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.

Понятие плоскости и ее обозначения

Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.

В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.

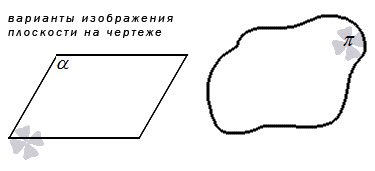
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.

Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.

Как могут располагаться плоскость и точка друг относительно друга

Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:

В любой плоскости есть точки.

Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.

Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.

Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:

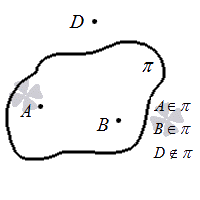
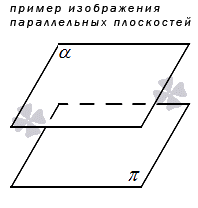
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.

Графически последнюю аксиому можно представить так:

Варианты взаимного расположения прямой и плоскости

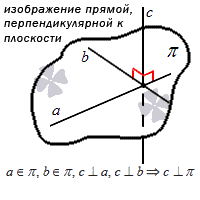
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:

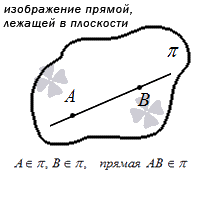
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.

Графически этот вариант расположения выглядит так:

Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.

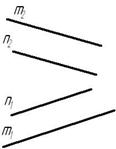
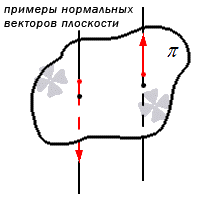
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.

Примеры нормальных векторов плоскости показаны на рисунке:

Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.

Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.

Варианты расположения двух плоскостей друг относительно друга

1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.

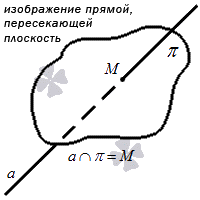
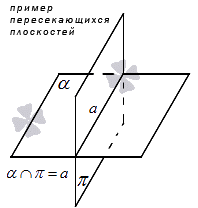
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:

Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.

На графике это будет выглядеть так:

В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.

3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.

Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.

Как задать плоскость в пространстве

В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.

1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.

Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:

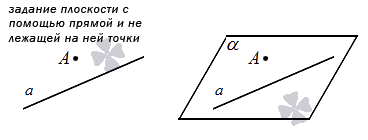
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:

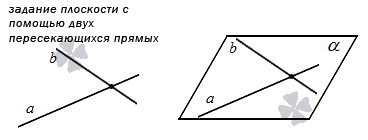
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:

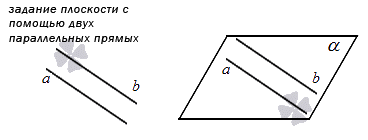
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.

На рисунке этот способ будет выглядеть так:

Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:

Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.

Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).

Вспомним одну теорему, изученную в рамках курса по геометрии:

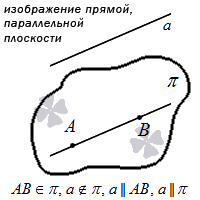
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.

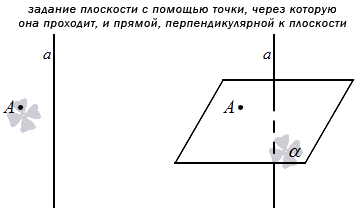
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.

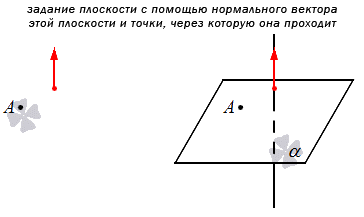
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.

Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.

Источник

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Источник