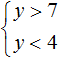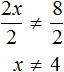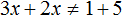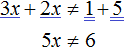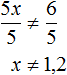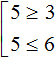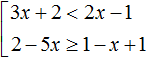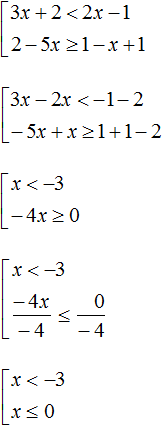Как записать что элемент принадлежит не принадлежит множеству
Элементы, не принадлежащие множеству. Пересечение множеств
Урок 12. Информатика 3 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Элементы, не принадлежащие множеству. Пересечение множеств»
Мы уже знаем, объекты можно объединять в группы и такое объединение в информатике и математике называется множеством. Любое множество можно изобразить в виде замкнутой фигуры. И элементы, которые принадлежат этому множеству, будут находиться внутри этой замкнутой фигуры.
Третьеклассники, брат и сестра Яна и Миша никогда вместе домашнее задание не делали. Вот и на этот раз выполняли домашнее задание по информатике порознь.
Давайте посмотрим, что это за задание, и как Яна и Миша его выполнили.
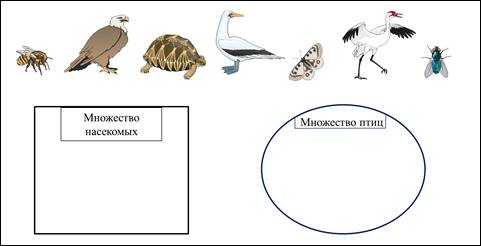
Необходимо распределить элементы по множествам.
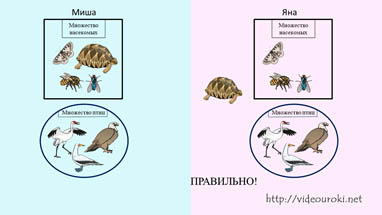
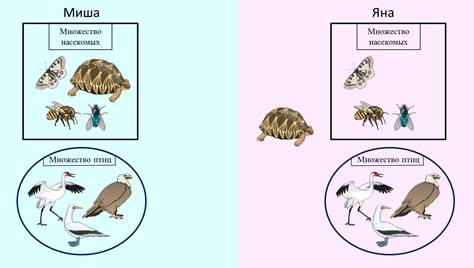
Вот так выполнил Миша, а вот так выполнила Яна.
Миша, говорит, что он сделал правильно, а Яна нет. Яна наоборот уверена, что она выполнила правильно, а её брат нет. Кто же правильно выполнил это задание, а кто нет, разберётся их учитель по информатике Ирина Ивановна. Она как раз сейчас другому третьему классу объясняет тему множества.
Проверив работы, Яне поставили «отлично», а Мише «удовлетворительно». Почему?
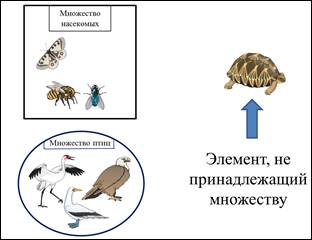
Посмотрим, какую ошибку допустил Миша? Миша включил черепаху во множество насекомых, а ведь черепаха это не насекомое и не птица, это рептилия. Так у нас же нет такого множества? А как это так? Может черепаха случайно попала в список элементов?
Нет. Оказывается, могут быть такие элементы, которые не принадлежат множеству. И такие элементы размещают вне замкнутой фигуры. В задании, которое выполняли Яна и Миша, таким элементом является черепаха, которая не принадлежит множеству птиц и не принадлежит множеству насекомых. Значит, черепаха будет размещаться вне этих множеств.
Ну, надеемся, Миша свою ошибку понял. А давайте, чтобы это проверить, попросим его выполнить ещё одно задание.
В одну таблицу записать элементы, которые принадлежат множеству, а в другую – которые не принадлежат этому множеству, а ещё придумать имя для множества.
Ну, посмотрим, как Миша выполнил задание.
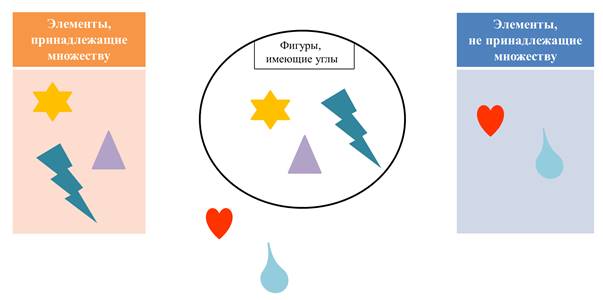
Правильно! Элементы, принадлежащие множеству, это: звезда, треугольник и молния.
Элементы, не принадлежащие множеству, это: сердце и капля.
А множество можно назвать: фигуры, имеющие углы.
А как вы думаете, существуют ли “хитренькие” элементы, которые умудряются жить сразу в двух множествах или даже трёх?
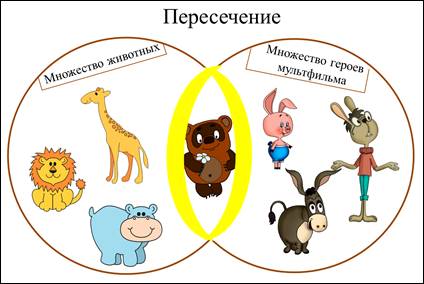
Как вы думаете, в каких множествах живёт Винни-Пух?
Во множестве животных и множестве героев мультфильма.
А в каких множествах живёт тигр? Во множестве хищников и во множестве полосатых животных.
Если один или несколько элементов входят в несколько множеств одновременно, то такие два множества пересекаются. Эти элементы отвечают основным признакам всех множеств, в которые он включён. На схеме границы таких множеств образуют общую область, которая называется пересечением.
Значит, пересечение множеств – это множество, состоящее из элементов, которые принадлежат одновременно всем данным множествам.
Давайте посмотрим задания, которые предлагает Ирина Ивановна, учитель Яны и Миши.
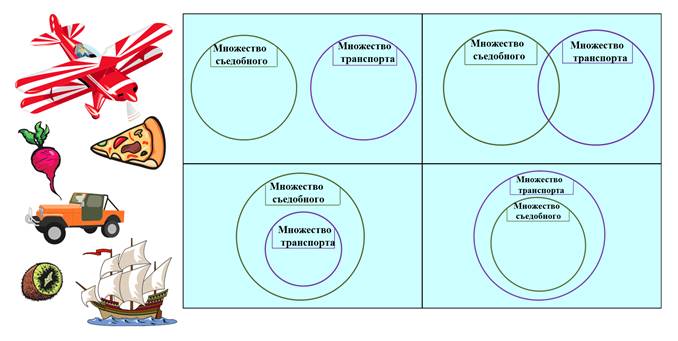
Распределить элементы по соответствующим множествам, обращая внимание на то, что некоторые элементы будут находиться на пересечении множеств.
Ну что, попробуем выполнить это задание.
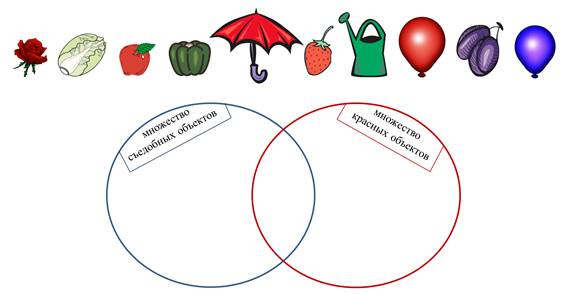
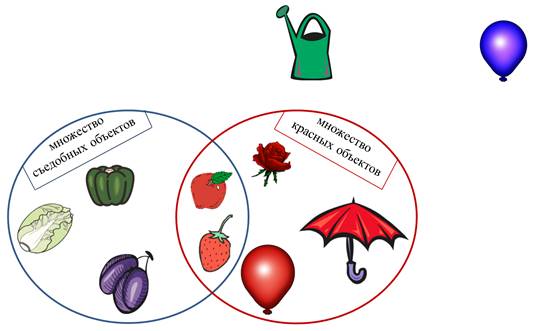
Итак, есть два множества: множество съедобных объектов и множество красных объектов.
Роза не съедобная, но красная. Помещаем во множество красных объектов.
Капуста: съедобная, но не красная. Помещаем во множество съедобных объектов.
Яблоко. Оно съедобное, значит, его можно отнести во множество съедобных объектов. Но, оно ведь ещё и красное, и мы можем отнести его во множество красный объектов. Значит, если яблоко и съедобное, и красное, оно будет находиться на пересечении двух множеств.
Перец: съедобный, но этот перец не красный. Значит, помещаем его во множество съедобных объектов.
Зонт: конечно, он не съедобный, наш зонт красный.
Клубника: съедобная и красная. Значит, она, как и яблоко, будет находиться на пересечении двух множеств.
Лейка. М-м-м, лейка не съедобная и не красная. Ага, мы уже знаем, что бывают элементы, не принадлежащие множеству. Это и есть такой элемент.
Воздушный шарик: он не съедобный, но красный. И его место во множестве красных объектов.
Слива: конечно съедобная, но не красная. Её место во множестве съедобных объектов.
Опять воздушный шарик: он не съедобный и не красный. Это ещё один элемент, не принадлежащий множеству.
Итак! Сколько элементов оказалось на пересечении двух множеств, т.е. одновременно в двух множествах? Два: яблоко и клубника.
Почему они оказались «хитренькими» элементами, которые умудрились расположиться сразу в двух множествах? А всё потому, что они одновременно и съедобными, и красными.
Кроме «хитреньких» бывают «скромные» и «порядочные» элементы, которым очень удобно жить в своём одном множестве, и в другие они попасть совсем не стремятся.
И есть «свободные» элементы, которые не принадлежат никакому множеству. Это лейка и синий воздушный шарик.
А давайте ещё посмотрим примеры с «порядочными» и «скромными» элементами.
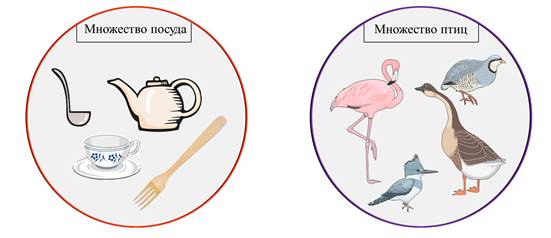
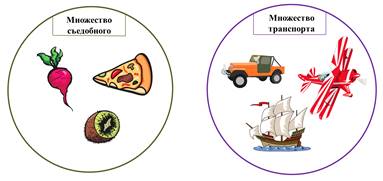
Черпак, заварник, чашка, вилка. Можно объединить во множество посуда.
Фламинго, куропатка, гусь, удод. Можно объединить во множество птиц.
Если ни один элемент множества не входит в другое множество, то такие множества не пересекаются и на схеме общих областей не образуют.
̶ Ой, ̶ говорит Миша. Так много новой информации. А давайте, ещё выполним несколько заданий, чтобы на следующем уроке я смог получить отметку, как у моей сестры Яны.
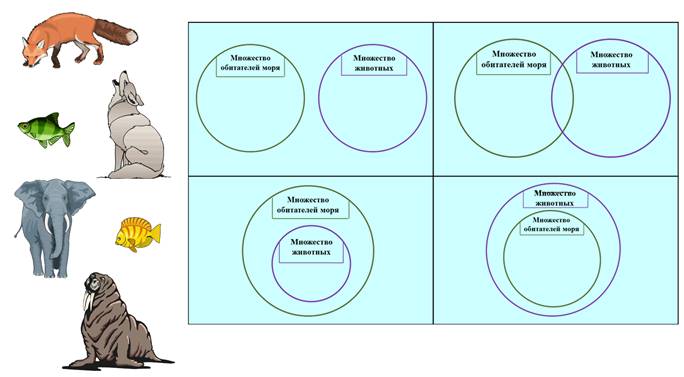
Посмотри на все элементы, найди правильное отношение между множествами и распредели элементы по множествам.
Итак. Подумаем, как мы распределим элементы и найдём правильное отношение между множествами.
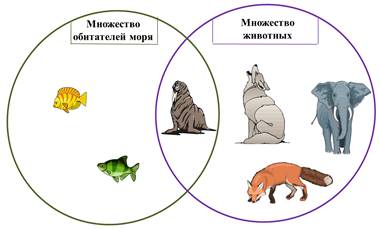
Конечно, здесь будет пересечение. Ведь морж, является и животным и обитателем моря.
Ещё несколько объектов надо разместить по своим множествам.
Внимательно посмотрим на объекты, на отношения между множествами и найдём правильное. Конечно, эти множества пересекаться не будут, все элементы будут располагаться только в своих множествах.
«А давайте ещё выполним задание, которое я придумал сам», ̶ говорит Миша.
Ну, что ребята выполним это задание?
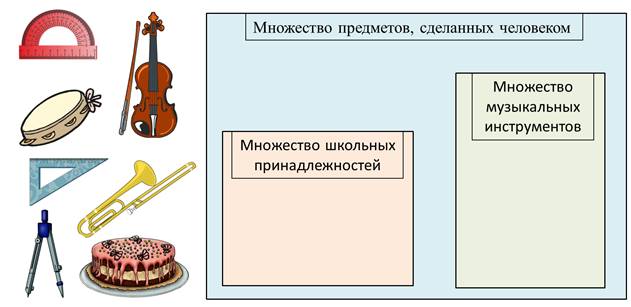
Разместить элементы в свои множества. Ага, Миша думал, мы не знаем про существование подмножеств и не выполним это задание.
Знаем мы, Миша, что множество школьных принадлежностей и множество музыкальных инструментов являются подмножеством множества предметов, сделанных человеком. Ну, давайте размещать объекты в свои множества.
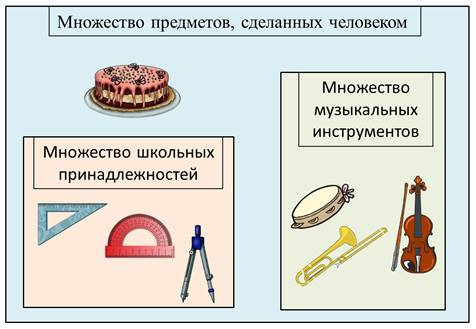
Транспортир, линейка, циркуль – это школьные принадлежности.
Скрипка, бубен и труба – это музыкальные инструменты.
И остался торт, конечно, он сделан руками человека, но это не музыкальный инструмент и не школьные принадлежности. Значит, размещаем его во множество предметов, сделанных человеком.
Задания мы все выполнили, теперь давайте вспомним, какие знания мы получили на уроке?
Сегодня мы встретились с ситуацией, когда два множества пересекаются: на пересечении находятся элементы, которые мы назвали «хитренькими».
Познакомились со «скромными» и элементами, которые живут только в своих множествах и поэтому множества не пересекаются. А ещё узнали, что есть «свободные» элементы, которые не принадлежат никакому множеству.
̶А я хочу пожелать, ̶ говорит Миша, ̶ чтобы в вашем множестве отметок такой элемент как двойка никогда не встречался!
Операции над множествами
Пересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда :
| Общие друзья Джона и Майкла | = |
В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Пример 4. Найти пересечение следующих множеств:
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6) :
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8] :
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7] :
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Пример 7. Дано множество из одного элемента < 2 >. Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента < 2 >, на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества < 2 >и числового промежутка (−3; 4) будет множество, состоящее из одного элемента < 2 >, поскольку элемент 2 принадлежит как множеству < 2 >, так и числовому промежутку (−3; 4)
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств. Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств 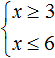
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
Пример 2. Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
Запишем ответ к системе 
Пример 3. Решить неравенство
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
Итак, у нас имеются следующие исходные множества:
Зададим новое множество С и добавим в него все элементы множества A
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.
| Все друзья Джона и Майкла | = |
В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
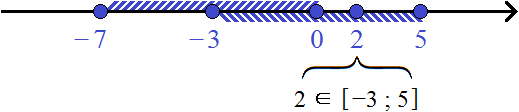
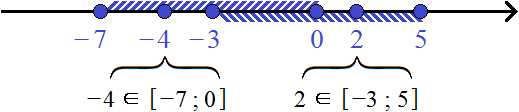
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2 ; −1] и [4 ; 7].
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Решение неравенств, содержащих знак ≠
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности 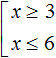
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
Пример 2. Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств 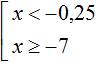
Иначе говоря, решением совокупности 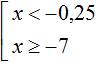
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
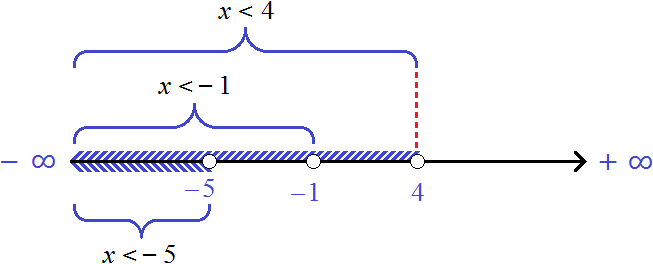
Пример 3. Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Решением совокупности неравенств 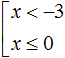
Иначе говоря, решением совокупности 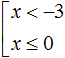
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее: