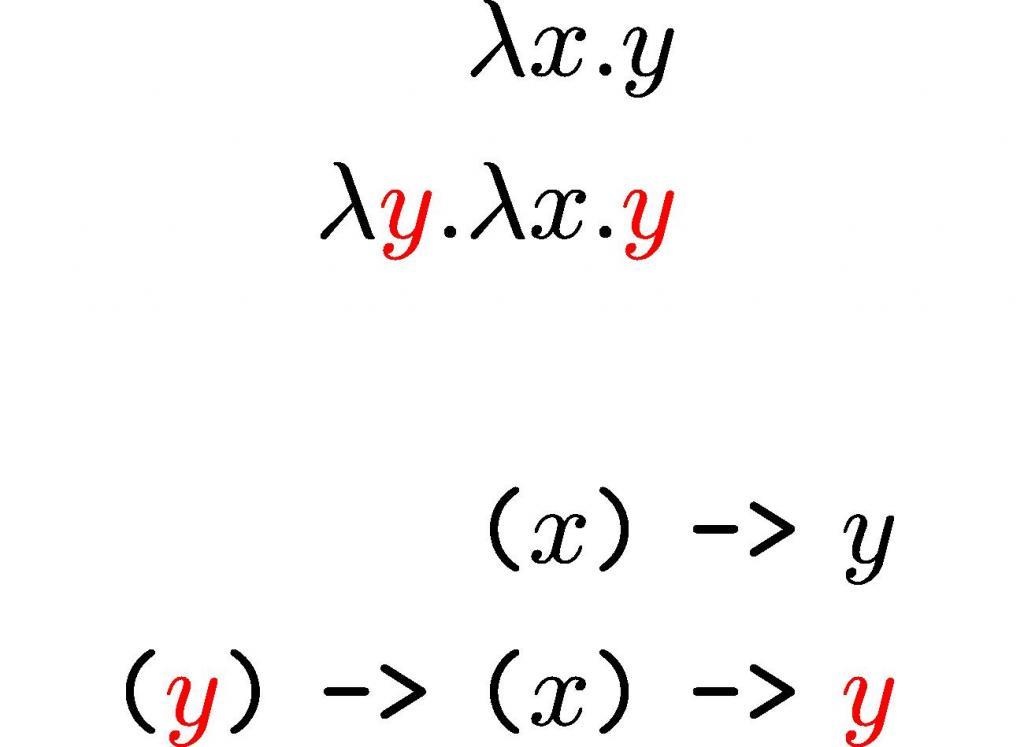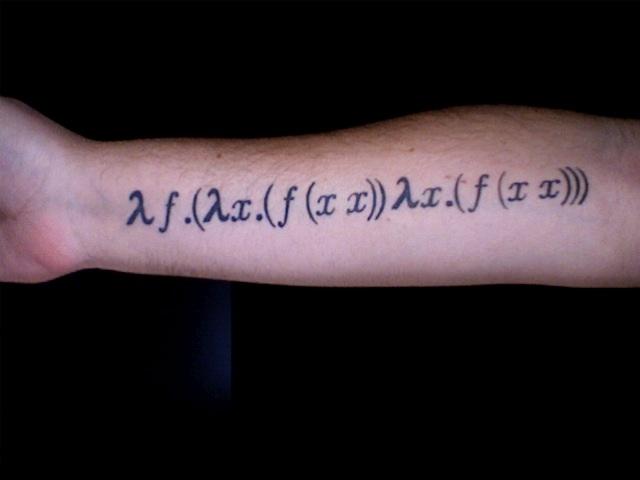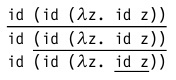Лямбда что это в математике
Лямбда-исчисление: описание теоремы, особенности, примеры
Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.
Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.
Пояснения и приложения

Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.
Лямбда-исчисление может быть нетипизировано или напечатано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.
Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.

Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.
Для чайников
Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.
В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.

До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.
Происхождение символа
Лямбда не обозначает слово или аббревиатуру, она возникла, благодаря ссылки в «Принципиальной математике» Рассела, за которой следуют два типографских изменения. Пример обозначения: для функции f с f (y) = 2y + 1 равно 2ŷ + 1. И здесь используется символ каретки («шляпа») над y для пометки входной переменной.
Церковь изначально намеревалась использовать аналогичные символы, но наборщики не смогли разместить символ «шляпа» над буквами. Поэтому вместо этого они напечатали его изначально как «/y.2y+1». В следующем эпизоде редактирования наборщики заменили «/ » на визуально похожий символ.
Введение в лямбда исчисление
Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.
Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.
Лямбда-термины
Синтаксис исчисления определяет некоторые выражения как допустимые, а другие — как недействительные. Также, как различные строки символов являются допустимыми программами на Си, а какие-то — нет. Действительное выражение лямбда-исчисления называется «лямбда-термином».
Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:
Переменная x сама по себе является действительным лямбда-термином:
Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.
Определение

Лямбда-выражения состоят из:
Множество Λ, может быть определено индуктивно:
Обозначение
Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:
Свободные и связанные переменные
Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.
Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:
Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.
Сокращение
Значение лямбда-выражений определяется тем, как они могут быть сокращены.
Существует три вида урезания:
Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.
Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:
(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].
Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.
α-преобразование
Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.
Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.
Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.
В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.
В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.
Замена
y [x: = N] ≡ y, если x ≠ y
(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])
(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).
Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.
β-редукция
Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ‘) является Е [V: = Е’].
Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.
Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.
η-преобразование
Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.

Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.
Нормальные формы и слияние
Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.
Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).
Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.
Дополнительные методы программирования
Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.
Именованные константы
В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,
Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.
Объединяя в цепочку такие определения, можно написать «программу» лямбда-исчисления как ноль или более дефиниций функций, за которыми следует один лямбда-член, используя те определения, которые составляют основную часть программы.
Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.
Печатные аналоги
Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.
Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.
Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.
λ-исчисление. Часть вторая: практика
Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.
Первая часть дала нам теоретическое представление о том, что есть лямбда-исчисление. В этой статье мы последуем неофициальной його-заповеди «Practice-practice-practice» и увидим его в действии.
Булевы константы Чёрча
Как уже говорилось ранее, в чистом бестиповом лямбда-исчислении отсутствует всё, кроме функций. Так что даже такие элементарные вещи, как числа или булевы значения необходимо реализовывать самим. Точнее, надо создать некие активные сущности, которые будут вести себя подобно необходимым нам объектам. И, естественно, процесс кодирования будет заключаться в написании соответствующих функций.
Посмотрим, как это будет работать:
if fls t e
Поскольку условие if ложно ( fls ), то должно возвращаться выражение из ветки else ( e в нашем случае).
| (λb. λx. λy. b x y) fls t e | по определению if |
| (λx. λy. fls x y) t e | редукция подчёркнутого выражения из предыдущей строки |
| (λy. fls t y) e | редукция подчёркнутого выражения из предыдущей строки |
| fls t e | редукция подчёркнутого выражения из предыдущей строки |
| (λt.λf. f) t e | по определению fls |
| (λf. f) e | редукция подчёркнутого выражения из предыдущей строки |
| e | редукция подчёркнутого выражения из предыдущей строки |
В определении основных булевых операторов тоже нет ничего сложного. Например, конъюнкция (логическое «и») будет выглядеть так:
and = λx. λy. x y fls
Определите логические «или» и «не».
Числа Чёрча
Мы с вами будем кодировать только натуральные числа, для чего вспомним аксиомы Пеано, определяющие их множество. В основе реализации по-прежнему будут лежать функции, ведущие себя в заданном контексте подобно единице, двойке и т.д. Собственно, это одна из особенностей лямбда-исчисления: сущности, записанные в его терминах, не обладают самодостаточностью, поскольку воплощают поведение того или иного объекта.
Итак, нам нужна функция, принимающая два аргумента: фиксированное начальное значение и функцию для определения следующего элемента (функцию следования). Число будет закодировано в количестве применений функции следования к начальному значению:
| 0 ≡ λs.λz. z | функция s применяется к начальному значению z нуль раз |
| 1 ≡ λs.λz. s z | функция s применяется к начальному значению z один раз |
| 2 ≡ λs.λz. s (s z) | функция s применяется к начальному значению z два раза |
| . | и так далее |
Легко заметить, что нуль кодируется так же, как и логическое False. Тем не менее, не стоит делать из этого какие-либо далеко идущие выводы: это всего лишь совпадение.
Арифметические операции
Сложение
plus = λx. λy. λs. λz. x s (y s z)
| plus one two s’ z’ | s’ и z’ — чтобы не путать подставляемые значения с именами переменных |
| (λx. λy. λs. λz. x s (y s z)) one two s’ z’ | по определению plus |
| one s’ (two s’ z’) | после проведения редукции |
| (λs.λz. s z) s’ (two s’ z’) | по определению one |
| s’ (two s’ z’) | после проведения редукции |
| s’ (( λs.λz. s (s z) s’ z’) | по определению two |
| s’ (s’ (s’ z’)) | после проведения редукции |
| three s’ z’ | по определению three |
Умножение
times = λx. λy. x (plus y) z
times’ = λx.λy.λs.λz. x (y s) z
| times’ two three s’ z’ | s’ и z’ — чтобы не путать подставляемые значения с именами переменных |
| (λx.λy.λs.λz. x (y s) z) two three s’ z’ | по определению times’ |
| two (three s’) z’ | после проведения редукции |
| (λs.λz. s (s z)) (three s’) z’ | по определению two |
| three s’ ((three s’) z’) | после проведения редукции |
| (λs.λz. s (s (s z))) s’ ((three s’) z’) | по определению three |
| s’ (s’ (s’ ((three s’) z’))) | после проведения редукции |
| s’ (s’ (s’ (((λs.λz. s (s (s z))) s’) z’))) | по определению three |
| s’ (s’ (s’ (( (λz. s’ (s’ (s’ z))) z’ ))) | после проведения редукции |
| s’ (s’ (s’ (s’ (s’ (s’ z’))))) | редукция подчёркнутого выражения |
| six s’ z’ | по определению six |
Определите терм для возведения числа в степень
Последней нерассмотренной операцией является вычитание — не самая тривиальная вещь на числах Чёрча. Желающие могут изучить её самостоятельно, например, по книге Бенжамина Пирса «Types and Programming Languages».
Цитата для привлечения внимания из вики-конспекта по лямбда-исчислению: «Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот».
Заключение
Как видим, технически ничего сложного в лямбда-исчислении нет: всё сводится к элементарным подстановкам и редукциям. Но столь малого набора инструментов вполне хватает, чтобы при желании реализовать активные сущности, ведущие себя подобно парам, спискам, рекурсивным функциям и т.п. Они будут достаточно громоздкими, но, как уже говорилось, λ-исчисление предназначено не для написания программ, а для исследования и спецификации языков программирования и систем типов. С чем, собственно, и прекрасно справляется.
λ-исчисление. Часть первая: история и теория
Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.
UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.
Вступление
Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)
Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.
Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.
Процесс вычисления
Рассмотрим следующий терм-применение:
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
который для простоты можно переписать как
(напомним, что id — это функция тождества вида λx.x )
В этом терме содержится три редекса:
Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.
Лямбда-исчисление
Лямбда-исчисление (англ. lambda calculus) — формальная система, придуманная в 1930-х годах Алонзо Чёрчем. Лямбда-функция является, по сути, анонимной функцией. Эта концепция показала себя удобной и сейчас активно используется во многих языках программирования.
Содержание
Лямбда-исчисление [ править ]
| Определение: |
| Лямбда-выражением (англ. [math]\lambda[/math] -term) называется выражение, удовлетворяющее следующей грамматике: |
Пробел во втором правиле является терминалом грамматики. Иногда его обозначают как @, чтобы он не сливался с другими символами в выражении.
В первом случае функция является просто переменной. Во втором происходит аппликация (применение) одной функции к другой. Это аналогично вычислению функции-левого операнда на аргументе-правом операнде. В третьем — абстракция по переменной. В данном случае происходит создание функции одного аргумента с заданными именем аргумента и телом функции.
[math] x\\ (x\ z)\\ (\lambda x.(x\ z))\\ (\lambda z.(\lambda w.((\lambda y.((\lambda x.(x\ z))\ y))\ w)))\\ [/math]
Приоритет операций [ править ]
Свободные и связанные переменные [ править ]
Связанными переменными называются все переменные, по которым выше в дереве разбора были абстракции. Все остальные переменные называются свободными.
Связанные переменные — это аргументы функции. То есть для функции они являются локальными.
α-эквивалетность [ править ]
и замкнуто относительно следующих правил:
[math] P=_\alpha P’ \Rightarrow \forall x \in V: \lambda x.P=_\alpha \lambda x.P’\\ P=_\alpha P’ \Rightarrow \forall Z \in \Lambda : P Z =_\alpha P’Z\\ P=_\alpha P’ \Rightarrow \forall Z \in \Lambda : Z P =_\alpha Z P’\\ P=_\alpha P’ \Rightarrow P’=_\alpha P\\ P=_\alpha P’ \ \& \ P’=_\alpha P» \Rightarrow P=_\alpha P»\\[/math]
β-редукция [ править ]
и замкнуто относительно следующих правил
[math]P\to _\beta P’ \Rightarrow \forall x\in V:\lambda x.P\to _\beta \lambda x.P’\\ P\to _\beta P’ \Rightarrow \forall Z\in \Lambda : P\ Z\to _\beta P’\ Z\\ P\to _\beta P’ \Rightarrow \forall Z\in \Lambda : Z\ P\to _\beta Z\ P'[/math]
Каррирование [ править ]
Нотация Де Брауна [ править ]
Грамматику нотации можно задать как:
Примеры выражений в этой нотации:
Переменная называется свободной, если ей соответствует число, которое больше количества абстракций на пути до неё в дереве разбора.
Определение [ править ]
Введём на основе лямбда-исчисления аналог натуральных чисел, основанный на идее, что натуральное число — это или ноль, или увеличенное на единицу натуральное число.
+1 [ править ]
Сложение [ править ]
Сложение двух чисел похоже на прибавление единицы. Но только надо прибавить не единицу, а второе число.
[math]n[/math] раз применить [math]s[/math] к применённому [math]m[/math] раз [math]s[/math] к [math]z[/math]
[math](\operatorname
[math](\operatorname
Умножение [ править ]
[math](\operatorname
Возведение в степень [ править ]
It’s a kind of magic
[math](\operatorname
Логические значения [ править ]
Стандартные функции булевой логики:
Ещё одной важной функцией является функция проверки, является ли число нулём:
Пара [ править ]
Вычитание [ править ]
В отличие от всех предыдущих функций, вычитание для натуральных чисел определено только в случае, если уменьшаемое больше вычитаемого. Положим в противном случае результат равным нулю. Пусть уже есть функция, которая вычитает из числа единицу. Тогда на её основе легко сделать, собственно, вычитание.
Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот.
Сравнение [ править ]
Комбинатор неподвижной точки [ править ]
Попробуем выразить в лямбда-исчислении какую-нибудь функцию, использующую рекурсию. Например, факториал.
Лямбда исчисление обладаем замечательным свойством: у каждой функции есть неподвижная точка!
Рассмотрим следующую функцию.
[math]\operatorname
[math]Y\ = \ \lambda f.(\lambda x.f(x\ x))\ (\lambda x.f(x\ x))[/math]
Деление [ править ]
Воспользовавшись идеей о том, что можно делать рекурсивные функции, сделаем функцию, которая будет искать частное двух чисел.
[math]\operatorname
И остатка от деления
[math]\operatorname
Проверка на простоту [ править ]
[math]\operatorname
Следующее простое число. [math]\operatorname
[math]\operatorname
[math]\operatorname
Списки [ править ]
Для работы со списками чисел нам понадобятся следующие функции:
[math]\operatorname
[math]\operatorname
Выводы [ править ]
На основе этого всего уже можно реализовать эмулятор машины тьюринга: с помощью пар, списков чисел можно хранить состояния. С помощью рекурсии можно обрабатывать переходы. Входная строка будет даваться, например, закодированной аналогично списку: пара из длины и числа, характеризующего список степенями простых. Я бы продолжил это писать, но уже на операции [math]\operatorname
[1, 2][/math] я не дождался окончания выполнения. Скорость лямбда-исчисления как вычислителя печальна.