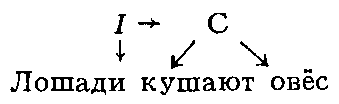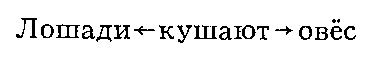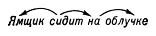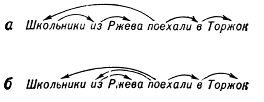Математическая лингвистика что это такое
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
Таким образом, можно выделить три аспекта формального описания языка: описание строения языковых объектов различных уровней, описание нек-рых специальных отношений и классификаций на множествах этих объектов и описание преобразований одних объектов в другие, а также строения множеств «правильных» объектов. Этим аспектам отвечают три основных раздела М. л.: 1) разработка и изучение способов описания строения отрезков речи; 2) изучение лингвистически значимых отношений и классификаций на множествах языковых объектов (построенные для этой цели формальные системы обычно называют аналитическими моделями языка);3) теория формальных грамматик.
Для описания строения отрезков речи используются синтаксич. структуры, представляющие собой графы или биграфы специального вида, обычно с помеченными вершинами и/или дугами. Лучше всего разработана теория описания «поверхностных» уровней (т. е. наиболее далеких от «смыслового»); на этих уровнях структуры обычно являются деревьями. Интенсивно разрабатываются способы описания более «глубинных» уровней. Для этого, в частности, предложен аппарат т. н. лексических функций, играющих при описании смысловой сочетаемости слов роль, сходную с той, к-рую традиционные категории рода, падежа, числа и т. п. играют при описании синтаксич. сочетаемости. Средств строгого описания «смыслового» уровня пока нет, но многим исследователям представляется вероятным, что на таком пути «последовательного приближения» можно надеяться выработать подход к формальному описанию смысла. Это не исключает и иных подходов; в частности, много исследований посвящено способам выражения в естественных языках предикатов, пропозициональных связок, кванторов, «переводу» с формально-логич. языков на естественные и обратно. Сюда же примыкают работы по конструированию так наз. семантических языков, в к-рых смыслы сопоставляются текстам простыми и строго формальными способами.
Аналитич. модели языка важны, в частности, ввиду того, что они позволяют уточнить логич. природу многих понятий и категорий традиционного языковедения. Эти модели не всегда носят характер эффективных процедур, поскольку в них могут входить такие понятия, как (бесконечное) множество грамматически правильных предложений нек-рого языка, считающееся заданным. Однако в ряде моделей все исходные данные представляют собой конечные множества и финитные отношения; в этих случаях входящие в модель процедуры эффективны. К теории аналитич. моделей языка примыкает теория лингвистической д е ш и ф р о в к и: ее предметом является построение процедур, применяемых, подобно аналитич. моделям, к «неупорядоченным» эмпирич. данным о языке, но всегда эффективных и позволяющих получать не только абстрактные определения, но и конкретные сведения о строении конкретных языков (напр., алгоритмы, осуществляющие автоматич. разбиение множества фонем языка на классы гласных и согласных без использования каких-либо сведений о языке, кроме нек-рого достаточно длинного текста).
Теория формальных грамматик наряду с «традиционными» для нее лингвистич. приложениями нашла применение в теории программирования для описания языков программирования и трансляторов. Особенно широко применяются для этих целей бесконтекстные грамматики, но используются и грамматики более общего вида.
Лит.:[1] Xомский Н., в кн.: Новое в лингвистике, в. 2, М., 1962, с. 412-527; [2] Гладкий А. В., Мельчук И. А., Элементы математической лингвистики, М., 1969.
Математическая лингвистика
Полезное
Смотреть что такое «Математическая лингвистика» в других словарях:
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков … Большой Энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА. Смежная для методики обучения языкам наука; раздел лингвистики, использующий математические методы исследования языка и речи. Данные М. л. применяются для проведения экспериментов в методике … Новый словарь методических терминов и понятий (теория и практика обучения языкам)
Математическая лингвистика — (также вычислительная лингвистика или компьютерная лингвистика) направление искусственного интеллекта, которое ставит своей целью использование математических моделей для описания естественных языков. Компьютерная лингвистика частично… … Википедия
математическая лингвистика — математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. * * * МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА, математическая дисциплина,… … Энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — математическая дисциплина, предметом к рой является разработка и изучение понятий, образующих основу формального аппарата для описания строения естественных языков (т. е. метаязыка лингвистики). Возникновение М. л. можно отнести приблизительно к… … Математическая энциклопедия
математическая лингвистика — 1. Изучает особенности семиотического и математического моделирования естественного языка (и речи) с целью перевода информации, содержащейся в неформализованном виде в тексте, на формализованный искусственный язык (например, на некоторый… … Толковый переводоведческий словарь
Математическая лингвистика — Математическая лингвистика математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Возникла в 50‑х гг. 20 в.; одним из главных стимулов появления… … Лингвистический энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — матем. дисциплина, предметом к рой является разработка формального аппарата для описания строения естественных и нек рых искусств, языков … Естествознание. Энциклопедический словарь
математическая лингвистика — Отрасль языкознания, занимающаяся изучением возможностей применения математических методов к изучений и описанию языка … Словарь лингвистических терминов
математическая лингвистика — Направление, возникшее в XX в. на стыке языкознания, математики и математической логики и занимающееся разработкой формального аппарата описания языка, применяемого в частности, в диалоге человек – ЭВМ … Словарь лингвистических терминов Т.В. Жеребило
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА, математическая дисциплина, разрабатывающая формальный аппарат для описания строения естественных и нек-рых искусственных языков. Возникла в 50-х гг. 20 в. в связи с назревшей в языкознании потребностью уточнения его осн. понятий. В М. л. используются по преимуществу идеи и методы алгебры, .алгоритмов теории и автоматов теории. Не являясь частью лингвистики, М. л. развивается в тесном взаимодействии с ней. М. л. называют иногда лингвистич. исследования, в к-рых применяется к.-л. математич. аппарат.
. Математические объекты, возникающие при таком описании структуры предложения, наз. деревом составляющих (1-й способ) и деревом синтаксического подчинения (2-й способ).
Формальные грамматики используются для описания не только естественных, но и искусственных языков, в особенности языков программирования.
М. л. изучает также аналитические модели языка, в к-рых на основе тех или иных данных о речи, считающихся известными (напр., множества правильных предложений), производятся формальные построения, дающие нек-рые сведения о структуре языка. Приложение методов М. л. к конкретным языкам относится к области лингвистики (см. Языкознание).
Лит.: Хомский Н., Синтаксические структуры, в сб.: Новое в лингвистике, в. 2, М., 1962; Гладкий А. В.. Мельчук И. А., Элементы математической лингвистики, М., 1969; Маркус С., Теоретико-множественные модели языков, пер. с англ., М., 1970; Гладкий А, В., Формальные грамматики и языки, М., 1973. А. В. Гладкий.
Смотреть что такое МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА в других словарях:
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
математическая дисциплина, разрабатывающая формальный аппарат для описания строения естественных и некоторых искусственных языков. Возникла в 5. смотреть
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
математическая дисциплина, предметом к-рой является разработка и изучение понятий, образующих основу формального аппарата для описания строения ес. смотреть
Математическая лингвистика
математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Возникла в 50‑х гг. 20 в.; одним из главных стимулов появления М. л. послужила назревшая в языкознании потребность уточнения его основных понятий. Методы М. л. имеют много общего с методами математической логики — математической дисциплины, занимающейся изучением строения математических рассуждений, — и в особенности таких её разделов, как теория алгоритмов и теория автоматов. Широко используются в М. л. также алгебраические методы. М. л. развивается в тесном взаимодействии с языкознанием. Иногда термин «М. л.» используется также для обозначения любых лингвистических исследований, в которых применяется какой-либо математический аппарат.
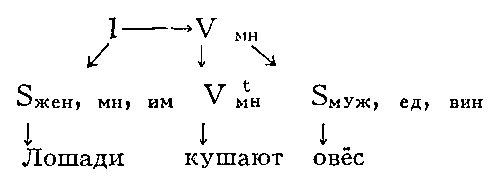
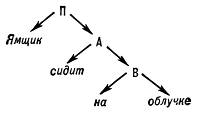
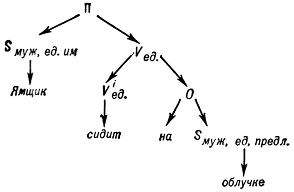
Математическое описание языка основано на восходящем к Ф. де Соссюру представлении о языке как механизме, функционирование которого проявляется в речевой деятельности его носителей; её результатом являются «правильные тексты» — последовательности речевых единиц, подчиняющиеся определённым закономерностям, многие из которых допускают математическое описание. Разработка и изучение способов математического описания правильных текстов (в первую очередь предложений) составляет содержание одного из разделов М. л. — теории способов описания синтаксической структуры. Для описания строения предложения — точнее, его синтаксической структуры — можно либо выделить в нём составляющие — группы слов, функционирующие как цельные синтаксические единицы, либо указать для каждого слова те слова, которые ему непосредственно подчинены (если такие есть). Так, в предложении «Ямщик сидит на облучке» (А. С. Пушкин) при описании по 1‑му способу составляющими будут все предложение П, каждое его отдельное слово и группы слов A = сидит на облучке и B = на облучке (см. рис. 1; стрелки означают «непосредственное вложение»); описание по 2‑му способу даёт схему, показанную на рис. 2. Возникающие при этом математические объекты называются системой составляющих (1‑й способ) и деревом синтаксического подчинения (2‑й способ).
Точнее, система составляющих — это множество отрезков предложения, содержащее в качестве элементов всё предложение и все вхождения слов в это предложение («однословные отрезки») и обладающее тем свойством, что каждые два входящих в него отрезка либо не пересекаются, либо один из них содержится в другом; дерево синтаксического подчинения, или просто дерево подчинения, есть дерево, множеством узлов которого служит множество вхождений слов в предложение. Деревом в математике называется множество, между элементами которого — их называют узлами — установлено бинарное отношение — его называют отношением подчинения и графически изображают стрелками, идущими от подчиняющих узлов к подчиненным, — такое, что: 1) среди узлов имеется точно один — его называют корнем, — не подчинённый никакому узлу; 2) каждый из остальных узлов подчинен точно одному узлу; 3) невозможно, отправившись из какого-либо узла вдоль стрелок, вернуться в тот же узел. Узлы дерева подчинения — это вхождения слов в предложения. При графическом изображении система составляющих (как на рис. 1) также приобретает вид дерева (дерева составляющих). Построенное для предложения дерево подчинения или систему составляющих часто называют его синтаксической структурой в виде дерева подчинения (системы составляющих). Системы составляющих используются преимущественно в описаниях языков с жёстким порядком слов, деревья подчинения — в описаниях языков со свободным порядком слов (в частности, русского), формально для каждого (не слишком короткого) предложения можно построить много разных синтаксических структур любого из двух видов, но среди них только одна или несколько являются правильными. Корнем правильного дерева подчинения служит обычно сказуемое. Предложение, имеющее более одной правильной синтаксической структуры (одного вида), называется синтаксически омонимичным; как правило, разные синтаксические структуры отвечают разным смыслам предложения. Например, предложение «Школьники из Ржева поехали в Торжок» допускает два правильных дерева подчинения (рис. 3, а, б); первое из них отвечает смыслу «Ржевские школьники поехали (не обязательно из Ржева) в Торжок», второе — «Школьники (не обязательно ржевские) поехали из Ржева в Торжок».
В русском и ряде других языков деревья подчинения предложений «делового стиля» подчиняются, как правило, закону проективности, состоящему в том, что все стрелки можно провести над прямой, на которой записано предложение, таким образом, что никакие две из них не пересекутся и корень не будет лежать ни под какой стрелкой. В языке художественной литературы, особенно в поэзии, отклонения от закона проективности допустимы и чаще всего служат задаче создания определённого художественного эффекта. Так, в предложении «Друзья кровавой старины народной чаяли войны» (Пушкин) непроективность приводит к эмфатическому выделению слова «народной» и одновременно как бы замедляет речь, создавая этим впечатление известной приподнятости, торжественности. Имеются и другие формальные признаки деревьев подчинения, которые могут использоваться для характеризации стиля. Например, максимальное число вложенных друг в друга стрелок служит мерой «синтаксической громоздкости» предложения (см. рис. 4).
Для более адекватного описания строения предложения составляющие обычно помечаются символами грамматических категорий («именная группа», «группа переходного глагола» и т. п.), а стрелки дерева подчинения — символами синтаксических отношений («предикативное», «определительное» и т. п.).
Аппарат деревьев подчинения и систем составляющих используется также для представления глубинно-синтаксической структуры предложения, которая образует промежуточный уровень между семантической и обычной синтаксической структурой (последнюю часто называют поверхностно-синтаксической).
Более совершенное представление синтаксической структуры предложения (требующее, однако, более сложного математического аппарата) дают системы синтаксических групп, в которые входят как словосочетания, так и синтаксические связи, причём не только между словами, но и между словосочетаниями. Системы синтаксических групп позволяют совмещать строгость формального описания строения предложения с гибкостью, присущей традиционным, неформальным описаниям. Деревья подчинения и системы составляющих являются предельными частными случаями систем синтаксических групп.
Другой важный тип формальной грамматики — доминационная грамматика, которая порождает множество цепочек, интерпретируемых обычно как предложения вместе с их синтаксическими структурами в виде деревьев подчинения. Грамматика синтаксических групп порождает множество предложений вместе с их синтаксическими структурами, имеющими вид систем синтаксических групп. Имеются также различные концепции трансформационной грамматики (грамматики деревьев), служащей не для порождения предложений, а для преобразования деревьев, интерпретируемых как деревья подчинения или деревья составляющих. Примером может служить Δ-грамматика — система правил преобразования деревьев, интерпретируемых как «чистые» деревья подчинения предложений, т. е. деревья подчинения без линейного порядка слов.
Особняком стоят грамматики Монтегю, служащие для одновременного описания синтаксических и семантических структур предложения; в них используется сложный математико-логический аппарат (так называемая интенсиональная логика).
Формальные грамматики находят применение для описания не только естественных, но и искусственных языков, в особенности языков программирования.
В М. л. разрабатываются также аналитические модели языка, в которых на основе тех или иных данных о речи, считающихся известными, производятся формальные построения, результатом которых является описание некоторых аспектов строения языка. В этих моделях обычно используется несложный математический аппарат — простые понятия теории множеств и алгебры; поэтому аналитические модели языка иногда называют теоретико-множественными. В аналитических моделях наиболее простого типа исходными данными служат множество правильных предложений и система окрестностей — совокупностей «слов», принадлежащих одной лексеме (например, <дом, до́ма, дому, домом, доме, дома́, домов, домам, домами, домах>). Простейшим производным понятием в таких моделях является замещаемость: слово a замещаемо на слово b, если всякое правильное предложение, содержащее вхождение слова a, остаётся правильным при замене этого вхождения вхождением слова b. Если а замещаемо на b и b на a, говорят, что a и b взаимозамещаемы. (Например, в русском языке слово «синий» замещаемо на слово «голубой»; слова «синего» и «голубого» взаимозамещаемы.) Класс слов, взаимозамещаемых между собой, называется семейством. Исходя из окрестностей и семейств, можно получить ряд других лингвистически значимых классификаций слов, одна из которых приблизительно соответствует традиционной системе частей речи. В другом типе аналитических моделей вместо множества правильных предложений используется отношение потенциального подчинения между словами, означающее способность одного из них подчинять себе другое в правильных предложениях. В таких моделях можно получить, в частности, формальные определения ряда традиционных грамматических категорий — например, формальное определение падежа существительного, представляющее собой процедуру, которая позволяет восстановить падежную систему языка, зная только отношение потенциального подчинения, систему окрестностей и множество слов, являющихся формами существительных.
В аналитических моделях языка используются простые понятия теории множеств и алгебры. К аналитическим моделям языка близки дешифровочные модели — процедуры, позволяющие по достаточно большому корпусу текстов на неизвестном языке без каких-либо предварительных сведений о нём получить ряд данных о его структуре.
По своему назначению М. л. является прежде всего инструментом теоретического языковедения. В то же время ее методы находят широкое применение в прикладных лингвистических исследованиях — автоматической обработке текста, автоматическом переводе и разработках, связанных с так называемым общением между человеком и ЭВМ.
ScienceHub #06: Компьютерная лингвистика
Продолжая поездки по лабораториям ученых, мы попали в компанию ABBYY, и побеседовали с Анатолием Старостиным, руководителем группы семантического анализа и преподавателем кафедры «Компьютерная лингвистика» в МФТИ. Он рассказал о работе своей группы, направлениях компьютерной лингвистики в ABBYY и кто такие онтоинженеры.
Для начала нужно определиться с терминологией. Итак, компьютерная лингвистика – это наука, с одной стороне, о языке, а с другой стороны – о том, как работать с языком (не всегда естественным) с помощью компьютерных методов. Это наука, возникшая на стыке лингвистики и computer science. Компьютерная лингвистика под разными углами рассматривает естественный, формальный язык. В центре этой науки понятие языка, которое можно рассматривать с разных сторон. Его можно рассматривать, например, формально. Есть еще такая область, как математическая лингвистика, она возникла раньше компьютерной и представляет собой раздел математики, в котором есть свои теоремы, доказательства, формальные объекты.
В компьютерной лингвистике важно, что всегда в центре стоит практическая конкретная задача, которую нужно решить. Например, синтаксический автоматический анализ, машинный перевод, распознавание речи.
Что такое синтаксический анализ: когда есть стандартная для школьников задача – определить, где в предложении какие члены, какие слова главные, а какие – подчиненные, но сделать это без участия человека, автоматическим способом. Для этого у компьютера на входе есть цепочка символов, которую нужно правильно проинтерпретировать, разбить на слова, связать их между собой и построить синтаксическое дерево. Так как структура предложения естественного языка – древесная, и это понятный факт из обычной, не компьютерной лингвистики.
Омоним как проблема
Основной трудностью в синтаксическом анализе является проблема омонимии, когда два слова одинаково пишутся, но имеют разное значение, в этом случае машина должна понять, что именно имеется в виду.
Анатолий Старостин: «Омонимия возникает и на следующих уровнях. Например, когда мы пытаемся понять, как слова связаны друг с другом, есть типичный пример предложения, который всегда приводят: «Эти типы стали есть на складе». В этом предложении все виды омонимии представлены. С одной стороны, мы слышим, что какие-то люди начали питаться на складе, а с другой стороны, что на складе есть разные типы металла. Это типы стали? Или типы начали? Эта омонимия слышна. И если рисовать синтаксические деревья, то в одном случае сказуемым является слово «стали» (то есть форма глагола «стать»), а в другом случае сказуемым является слово «есть». Соответственно, если нарисовать два дерева, они будут разными. Это пример синтаксической омонимии».
Проблема в том, как автоматическим способом считывать контекст предложения и решать омонимы. Это одно из направлений в компьютерной лингвистике.
История
Компьютерная лингвистика как направление возникла в середине XX века. И первой задачей стразу стало сильно амбициозное по тем временам желание создать программу по автоматического перевода текста. При этом надо помнить, что компьютеры не отличались мощностью. И со временем люди пришли к осознанию того, насколько сложна эта задача.
Одновременно с этим было популярно направление, которое называется искусственный интеллект. Люди хотели, чтобы компьютер решал интеллектуальные задачи. Хотя искусственный интеллект – это более широкая область, чем компьютерная лингвистика, обработка естественного языка рассматривалась как его часть.
А. С. :«В какой-то момент был бум методов машинного обучения. Он случился, когда люди поняли, что с помощью методов математической статистики и специальных алгоритмов можно делать так, чтобы компьютер достаточно точно воспроизводил какое-то интеллектуальное поведение человека. Могу привести пример задачи, которая по сей день очень актуальна. Это задача нахождения в текстах именованных сущностей, когда нужно найти в тексте все упоминания персон или все упоминания организаций. Оказывается, что эту задачу можно решать аналитически (писать правила, сложные алгоритмы). А можно решать эту задачу другим образом, взяв пачку текстов, разметить в ней руками, где персоны, а где организации. После этого дать ее компьютеру, сказать: «Посмотри, в этих текстах персоны здесь, а организации – здесь». И с помощью методов научного обучения компьютер может впитать в себя это знание. И на других текстах, которые он до этого еще не видел, это повторить с довольно высокой точностью. То есть, он возьмет другой текст, которого он еще раньше не читал, и по аналогии с теми текстами угадает, где там упоминание персон, где – организаций. В этот момент он, естественно, воспользуется некоторыми признаками, которые он сам выучил. Эти признаки: большие буквы, какие-то морфологические формы. Есть разные зацепки и крючки, которые в тексте на самом деле есть. Мы читаем, понимаем, что это персона. А на самом деле персона обычно употребляется в таких-то контекстах. Мы даже этого не знаем. А компьютер с помощью метода машинного обучения может в себя впитать эти контексты и воспроизвести. Когда люди это поняли, возникло очень много приложений на базе машинного обучения. Методы машинного обучения сегодня очень существенная часть компьютерной лингвистики применительно к задачам анализа текстов с разных сторон. С помощью машинного обучения решается очень много разных задач».
Профессия «компьютерный лингвист»
Есть несколько основных профессий, использующихся для компьютерной лингвистики. Одна профессия – это программист. Другое дело, что обычно все программисты приходят работать недоученными, и их нужно доучивать. Но нужны и лингвисты, потому что они носители знаний о естественном языке. Лингвисты, попадая в зону компьютерной лингвистики, тоже должны получить новые знания, стать более структурными и формальными для работы в Computer science.
А. С.: «Компьютерная лингвистика предполагает сотрудничество лингвистов и программистов. И они идут друг другу навстречу. Программисты, которые занимаются компьютерной лингвистикой, поскольку они описывают объект, должны в нем разобраться. Любой программист, например, у нас (в ABBYY), понимает, что такое синтаксическое дерево, понимает, как слова связываются друг с другом, много знает о лингвистике, понимает, что такое род, число, падеж. И у нас в ABBYY в чистом виде делают специальные уровни абстракции. То есть, для лингвистов создают какие-то формальные языки, среды, внутри которых они работают, и которые приближены к их взгляду на мир. Они приближены к языку, естественно. И лингвисты варятся в этих средах. Но при этом все равно они хорошо знают, что здесь они сейчас напишут такое-то правило. И это правило будет подхвачено таким-то алгоритмом и так-то использовано. Такие представления у лингвистов есть. Без этого они не смогли бы работать. Подготовка лингвистов с оглядкой на компьютерную лингвистику существенно влияет и на самих лингвистов. Более или менее современные лингвисты сегодня (если говорить о людях, которые занимаются естественным языком, пишут теоретические работы об этом), давно перешли на представления о компьютерных методах».
Онтоинженеры в ABBYY
Базовый лингвистический компонент, который является фундаментом технологии Compreno, разрабатывают в ABBYY последние много лет. Это программа, которая строит семантико-синтаксические деревья.
Используя базовую прослойку, которая любое предложение на естественном языке превращает в семантико-синтаксическое дерево, можно решать более высокоуровневые задачи. В частности извлечение информации. Это разные аббревиатуры, в основном англоязычные, но они все имеют и русские аналоги. Собственно это комплекс задач вокруг анализа информации. Если на входе есть текст, то нужно его определенным образом проинтерпретировать. Этим Анатолий и занимается в своей группе в ABBYY.
А.С.: «Если говорить чуть детальней, что значит определенным образом проинтерпретировать и что-то извлечь? Задачи изучения информации всегда ставятся следующим образом. Первым делом описывается модель предметной области. То есть, мы всегда знаем, какую задачу мы решаем. И формально это фиксируем. Эта модель предметной области еще называется онтологией. Мы заранее рисуем, что нас интересуют, к примеру, персоны: организации, факты работы персон в организациях. Или нас интересуют локации: факты расположения организаций в локациях. То есть, мы рисуем концептуальную схему предметной области. И под призмой этой концептуальной схемы рассматриваем текст. То есть нам нужно из текста извлечь не всю информацию, которая есть в тексте (что было бы абсолютно неопределенно, потому что в любом тексте очень много разной информации). Нам нужно извлечь только ту информацию, которая укладывается в полочки, которые мы себе заранее нарисовали. Так ставятся задачи изучения информации».
Сами онтологии бывают очень разные, обычно они тематические. Это может быть онтология медицины, бизнеса, это может быть онтология спорта. Всегда сначала описывается онтология. Дальше начинается разработка. Это делают специальные люди, которые называются онтоинженерами.
Онтоинженеры — хороший пример симбиоза лингвиста и программиста, обычно, это выпускники математических вузов, потому что они должны хорошо концептуализировать действительность, разбивать задачи на подзадачи, понимать, где какие сущности, как они связаны. С другой стороны, они должны хорошо представлять себе, что такое семантико-синтаксические деревья, то есть иметь лингвистические знания.
А. С.: «Онтоинженеры садятся и на высокоуровневом языке пишут правила. На входе этот язык получает семантико-синтаксические деревья, а на выходе порождает концептуальный граф соответствующей модели предметной области. Простой пример, у вас в компании есть персоны, организация и факты работы. И у вас есть предложение «Вася работает в ABBYY». Программа должна извлечь персону «Вася» (то есть конкретный экземпляр концепта персоны), извлечь организацию ABBYY (конкретный экземпляр концепта организация) и понять, что эти два экземпляра связаны между собой отношением работы. Это типичный пример извлечения информации. Сложность здесь в том, что в естественном языке один и тот же концепт можно выражать очень разными способами. Это всегда огромное многообразие способов сказать одно и то же. Можно сказать: «Вася сотрудник ABBYY». Можно сказать: «Вася работает в ABBYY». Можно сказать: «Вася был уволен из ABBYY», и это все равно будет значит, что он когда-то был сотрудником. Можно сказать: «Вася работает в ABBYY на полставки». Все эти фразы надо понять и свести к общему знаменателю. Вот задача извлечения информации в модельном виде».
Если подытожить, что можно сказать, что компьютерная лингвистика становится инструментом извлечения информации оттуда, откуда раньше ее не могли извлечь.
А.С. :«Если кто-то положил в структурированную базу данных, мы взять можем, потому что они структурированы. Надо только разобраться в формате, то есть в том, как они их выложили. А если это написано текстом, то, казалось бы, это может понять только человек. Оказывается, что с помощью таких методов можно написать программы, которые поймут вместо человека. Это, грубо говоря, конвертеры неструктурированной информации в структурированную. Вот что мы создаем в рамках моей группы в ABBYY».
Все то же самое, но в видео формате можно узнать здесь.