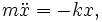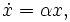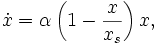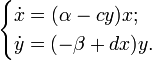Математическая модель что это такое

Математическая модель

Процесс построения и изучения математических моделей называется математическим моделированием.

Все естественные и общественные науки, использующие математический аппарат, по сути, занимаются математическим моделированием: заменяют объект исследования его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект или процесс, построенный на этапе содержательного моделирования. Математическая модель позволяет предсказать поведение реального объекта.

Связанные понятия

Компьютерная модель (англ. computer model), или численная модель (англ. computational model) — компьютерная программа, работающая на отдельном компьютере, суперкомпьютере или множестве взаимодействующих компьютеров (вычислительных узлов), реализующая представление объекта, системы или понятия в форме, отличной от реальной, но приближенной к алгоритмическому описанию, включающей и набор данных, характеризующих свойства системы и динамику их изменения со временем.

Упоминания в литературе

Связанные понятия (продолжение)

В математике решение дифференциального уравнения (или, шире, траектория в фазовом пространстве точки состояния динамической системы) называется устойчивым, если поведение решений, с условиями, близкими к начальным, «не сильно отличается» от поведения исходного решения. Слова «не сильно отличается» при этом можно формализовать по-разному, получая разные формальные определения устойчивости: устойчивость по Ляпунову, асимптотическую устойчивость и т.д. (см. ниже). Обычно рассматривается задача об устойчивости.

К критическим явлениям относятся многочисленные аномалии, наблюдающиеся в фазовых переходах второго рода, например, в точке Кюри в магнетике или в критической точке системы «жидкость-пар». Эти аномалии описываются критическими индексами. В системах появляются очень сильные флуктуации с бесконечным радиусом корреляции. При этом система существенно нелинейна.

Источник

Что такое математическая модель?

Понятие математической модели.

Например, нам нужно посчитать расходы (Р) на покупки в магазине. Надо купить две булки (Б) и три пачки масла (М). Мы знаем цену булки (ЦБ) и цену масла (ЦМ). Легко можно записать:

Составление (построение) математической модели задачи.

Говоря конкретнее, нужно установить математическую связь между всеми данными задачи.

Но можно выделить три основных момента, на которые нужно обратить внимание.

1. В любой задаче есть текст, как ни странно.) В этом тексте, как правило, имеется явная, открытая информация. Числа, значения и т.п.

3. В любой задаче должно быть дана связь данных между собой. Эта связь может быть дана открытым текстом (что-то равно чему-то), а может быть и скрыта за простыми словами. Но простые и понятные факты частенько упускаются из виду. И модель никак не составляется.

Сразу скажу: чтобы применить эти три момента, задачу приходится читать (и внимательно!) несколько раз. Обычное дело.

Начнём с простой задачки:

Все эти слова нужно превратить в какое-то уравнение. Для этого нужно, повторюсь, установить математическую связь между всеми данными задачи.

С чего начинать? Сначала вытащим из задачи все данные. Начнём по порядочку:

Обращаем внимание на первый момент.

Какая здесь явная математическая информация? 8 рыбин и 20%. Не густо, да нам много и не надо.)

Обращаем внимание на второй момент.

Ищем скрытую информацию. Она здесь есть. Это слова: «20% всех рыбин«. Здесь нужно понимать, что такое проценты и как они считаются. Иначе задача не решается. Это как раз та дополнительная информация, которая должна быть в голове.

Здесь ещё имеется математическая информация, которую совершенно не видно. Это вопрос задачи: «Сколько всего рыбин купил. « Это ведь тоже какое-то число. И без него никакая модель не составится. Поэтому обозначим это число буквой «х». Мы пока не знаем, чему равен икс, но такое обозначение очень нам пригодится. Подробнее, что брать за икс и как с ним обращаться, написано в уроке Как решать задачи по математике? Вот так сразу и запишем:

Возвращаемся к раскрытию информации. Кто не знает, что такое процент, никогда не раскроет, да. А кто знает, тот сразу скажет, что проценты здесь от общего числа рыб даны. А нам это число неизвестно. Ничего не выйдет!

Общее количество рыб (в штуках!) мы не зря буквой «х» обозначили. Посчитать южных рыб в штуках не получится, но записать-то мы сможем? Вот так:

Вот теперь мы скачали всю информацию с задачи. И явную, и скрытую.

Обращаем внимание на третий момент.

Ищем математическую связь между данными задачи. Эта связь настолько проста, что многие её не замечают. Такое часто бывает. Здесь полезно просто записать собранные данные в кучку, да и посмотреть, что к чему.

Вот это уравнение и будет математической моделью нашей задачи.

Прошу заметить, что в этой задаче нас не просят ничего складывать! Это мы сами, из головы, сообразили, что сумма южных и северных рыб даст нам общее количество. Вещь настолько очевидная, что проскакивает мимо внимания. Но без этой очевидности математическую модель не составить. Вот так.

Теперь уже можно применить всю мощь математики для решения этого уравнения). Именно для этого и составлялась математическая модель. Решаем это линейное уравнение и получаем ответ.

Составим математичесскую модель ещё одной задачки:

Спросили Петровича: «А много ли у тебя денег?» Заплакал Петрович и отвечает: «Да всего чуть-чуть. Если я потрачу половину всех денег, да половину остатка, то всего-то один мешок денег у меня и останется. » Сколько денег у Петровича?

Опять работаем по пунктам.

2. Ищем скрытую информацию. Это половинки. Чего? Не очень понятно. Ищем дальше. Есть ещё вопрос задачи: «Сколько денег у Петровича?» Обозначим количество денег буквой «х»:

И вновь читаем задачу. Уже зная, что у Петровича х денег. Вот тут уже и половинки сработают! Записываем:

Остаток будет тоже половина, т.е. 0,5·х. А половину от половины можно записать так:

Теперь вся скрытая информация выявлена и записана.

3. Ищем связь между записанными данными. Здесь можно просто читать страдания Петровича и записывать их математически):

Если я потрачу половину всех денег.

да половину остатка.

Отнимем ещё половину остатка:

то всего-то один мешок денег у меня и останется.

А вот и равенство нашлось! После всех вычитаний один мешок денег остаётся:

Вот она, математическая модель! Это опять линейное уравнение, решаем, получаем:

Задачки, конечно, элементарные. Это специально, чтобы уловить суть составления математической модели. В некоторых задачах может быть гораздо больше данных, в которых легко запутаться. Это часто бывает в т.н. компетентностных задачах. Как вытаскивать математическое содержание из кучи слов и чисел показано на примерах здесь.

В задачах на движение требуется держать в голове формулу-ключ: связь расстояния, скорости и времени. По ссылке можно посмотреть примеры составления модели и решения таких задач.

В задачах на работу надо чётко понимать формулу-ключ: связь времени, производительности труда и объёма работы. Там имеются свои фишки, с которыми можно ознакомиться по ссылке.

Для того, чтобы свободнее ориентироваться в построении математических моделей очень полезно порешать обратные задачи. Т.е. по заданной модели придумать условие задачи. Это, кстати, не так просто.) Тема может быть совершенно любой, фантазия ограничена только математикой. Вот примеры таких заданий:

Составить задачу по математической модели:

х + (х+10) + (х-30) + 20 = 120

Попробуйте придумать задачку, а потом можете найти в уроке Как решать задачи по математике исходную задачу для этой модели. И сравните, для интереса.)

Еще пример, посложнее:

Составить задачу по математической модели:

Исходная задача и её решение приведены в уроке Решение задач на движение. Кстати, по ссылке подробно написано, как эту математическую модель составить.

Составить задачу по математической модели:

1 = 5 · (х + 2х + 2х + 3х + 4х)

Эта задача и её решение расписаны в уроке Задачи на работу.

Ещё одно замечание. В классических школьных задачах (трубы заполняют бассейн, куда-то плывут катера и т.п.) все данные, как правило, подобраны очень тщательно. Там выполняются два правила:
— информации в задаче хватает для её решения,
— лишней информации в задаче не бывает.

В компетентностных и прочих жизненных задачах эти правила строго не соблюдаются. Нету подсказки. Но и такие задачи можно решать. Если, конечно, потренироваться на классических.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Математическое моделирование

Математическое моделирование — процесс построения и изучения математических моделей.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его математической моделью и затем изучают последнюю.

Содержание

Определения

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

Определение модели по А. А. Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):

По учебнику Советова и Яковлева [3] : «модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.» (с. 6) «Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием.» (с. 6) «Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.»

Несколько менее общее определение математической модели, основанное на идеализации «вход — выход — состояние», заимствованной из теории автоматов, даёт Wiktionary: «Абстрактное математическое представление процесса, устройства или теоретической идеи; оно использует набор переменных, чтобы представлять входы, выходы и внутренние состояния, а также множества уравнений и неравенств для описания их взаимодействия.» [6]

Наконец, наиболее лаконичное определение математической модели: «Уравнение, выражающее идею.» [7]

Классификация моделей

Формальная классификация моделей

Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий [8] :

и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т. д.

Классификация по способу представления объекта

Наряду с формальной классификацией, модели различаются по способу представления объекта:

Структурные модели представляют объект как систему со своим устройством и механизмом функционирования. Функциональные модели не используют таких представлений и отражают только внешне воспринимаемое поведение (функционирование) объекта. В их предельном выражении они называются также моделями «чёрного ящика» [12] Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».

Содержательные и формальные модели

Содержательная классификация моделей

В работе Р. Пайерлса (англ. R. Реiеrls ) [17] дана классификация математических моделей, используемых в физике и, шире, в естественных науках. В книге А. Н. Горбаня и Р. Г. Хлебопроса [18] эта классификация проанализирована и расширена. Эта классификация сфокусирована, в первую очередь, на этапе построения содержательной модели.

Тип 1: Гипотеза (такое могло бы быть)

Эти модели «представляют собой пробное описание явления, причем автор либо верит в его возможность, либо считает даже его истинным». По Р. Пайерлсу это, например, модель Солнечной системы по Птолемею и модель Коперника (усовершенствованная Кеплером), модель атома Резерфорда и модель Большого Взрыва.

Никакая гипотеза в науке не бывает доказана раз и навсегда. Очень чётко это сформулировал Ричард Фейнман:

«У нас всегда есть возможность опровергнуть теорию, но, обратите внимание, мы никогда не можем доказать, что она правильна. Предположим, что вы выдвинули удачную гипотезу, рассчитали, к чему это ведет, и выяснили, что все ее следствия подтверждаются экспериментально. Значит ли это, что ваша теория правильна? Нет, просто-напросто это значит, что вам не удалось ее опровергнуть.» [19]

Если модель первого типа построена, то это означает что она временно признаётся за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.

Тип 2: Феноменологическая модель (ведем себя так, как если бы…)

Феноменологическая модель содержит механизм для описания явления. Однако этот механизм недостаточно убедителен, не может быть достаточно подтверждён имеющимися данными или плохо согласуется с имеющимися теориями и накопленным знанием об объекте. Поэтому феноменологические модели имеют статус вре́менных решений. Считается, что ответ всё ещё неизвестен и необходимо продолжить поиск «истинных механизмов». Ко второму типу Пайерлс относит, например, модели теплорода и кварковую модель элементарных частиц.

Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично, новое знание может постепенно прийти в противоречие с моделями-гипотезами первого типа и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешёл в первый тип. А вот модели эфира, проделали путь от типа 1 к типу 2, а сейчас находятся вне науки.

Идея упрощения очень популярна при построении моделей. Но упрощение бывает разным. Пайерлс выделяет три типа упрощений в моделировании.

Тип 3: Приближение (что-то считаем очень большим или очень малым)

Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений (моделей типа 3). Среди них модели линейного отклика. Уравнения заменяются линейными. Стандартный пример — закон Ома.

Если мы используем модель идеального газа для описания достаточно разреженных газов, то это — модель типа 3 (приближение). При более высоких плотностях газа тоже полезно представлять себе более простую ситуацию с идеальным газом для качественного понимания и оценок, но тогда это уже тип 4.

Тип 4: Упрощение (опустим для ясности некоторые детали)

В модели типа 4 отбрасываются детали, которые могут заметно и не всегда контролируемо повлиять на результат. Одни и те же уравнения могут служить моделью типа 3 (приближение) или 4 (опустим для ясности некоторые детали) — это зависит от явления, для изучения которого используется модель. Так, если модели линейного отклика применяются при отсутствии более сложных моделей (то есть не производится линеаризация нелинейных уравнений, а просто ищутся линейные уравнения, описываюшие объект), то это уже феноменологические линейные модели, и относятся они к следующему типу 4 (все нелинейные детали «для ясности» опускаем).

Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван-дер-Ваальса, большинство моделей физики твердого тела, жидкостей и ядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. Это приводит к моделям 4-го типа.

Тип 5: Эвристическая модель (количественного подтверждения нет, но модель способствует более глубокому проникновению в суть дела)

Эвристическая модель сохраняет лишь качественное подобие реальности и даёт предсказания только «по порядку величины». Типичный пример — приближение средней длины свободного пробега в кинетической теории. Оно даёт простые формулы для коэффициентов вязкости, диффузии, теплопроводности, согласующиеся с реальностью по порядку величины.

Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта — модель пятого типа. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой-нибудь черте.

Тип 6: Аналогия (учтём только некоторые особенности)

Тип 7: Мысленный эксперимент (главное состоит в опровержении возможности)

А. Эйнштейн был одним из великих мастеров мысленного эксперимента. Вот один из его экспериментов. Он был придуман в юности и, в конце концов, привел к построению специальной теории относительности. Предположим, что в классической физике мы движемся за световой волной со скоростью света. Мы будем наблюдать периодически меняющееся в пространстве и постоянное во времени электромагнитное поле. Согласно уравнениям Максвелла, этого быть не может. Отсюда юный Эйнштейн заключил: либо законы природы меняются при смене системы отсчета, либо скорость света не зависит от системы отсчета. Он выбрал второй — более красивый вариант. Другой знаменитый мысленный эксперимент Эйнштейна — Парадокс Эйнштейна — Подольского — Розена.

А вот и тип 8, широко распространенный в математических моделях биологических систем.

Тип 8: Демонстрация возможности (главное — показать внутреннюю непротиворечивость возможности)

Это тоже мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципам и внутренне непротиворечиво. В этом основное отличие от моделей типа 7, которые вскрывают скрытые противоречия.

Один из самых знаменитых таких экспериментов — геометрия Лобачевского (Лобачевский называл её «воображаемой геометрией»). Другой пример — массовое производство формально — кинетических моделей химических и биологических колебаний, автоволн и др. Парадокс Эйнштейна — Подольского — Розена был задуман как модель 7 типа, для демонстрации противоречивости квантовой механики. Совершенно незапланированным образом он со временем превратился в модель 8 типа — демонстрацию возможности квантовой телепортации информации.

В основе содержательной классификации — этапы, предшествующие математическому анализу и вычислениям. Восемь типов моделей по Р. Пайерлсу суть восемь типов исследовательских позиций при моделировании.

Пример

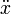
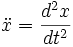
где означает вторую производную от x по времени: .

Полученное уравнение описывает математическую модель рассмотренной физической системы. Эта модель называется «гармоническим осциллятором».

По формальной классификация эта модель линейная, детерминисткая, динамическая, сосредоточенная, непрерывная. В процессе её построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т.

д.), которые в реальности могут не выполняться.

По отношению к реальности это, чаще всего, модель типа 4 упрощение («опустим для ясности некоторые детали»), поскольку опущены некоторые существенные универсальные особенности (например, диссипация). В некотором приближении (скажем, пока отклонение груза от равновесия невелико, при малом трении, в течение не слишком большого времени и при соблюдении некоторых других условий), такая модель достаточно хорошо описывает реальную механическую систему, поскольку отброшенные факторы оказывают пренебрежимо малое влияние на её поведение. Однако модель можно уточнить, приняв во внимание какие-то из этих факторов. Это приведет к новой модели, с более широкой (хотя и снова ограниченной) областью применимости.

Впрочем, при уточнении модели сложность её математического исследования может существенно возрасти и сделать модель фактически бесполезной. Зачастую более простая модель позволяет лучше и глубже исследовать реальную систему, чем более сложная (и, формально, «более правильная»).

Если применять модель гармонического осциллятора к объектам, далёким от физики, её содержательный статус может быть другим. Например, при приложении этой модели к биологическим популяциям, её следует отнести, скорее всего, к типу 6 аналогия («учтём только некоторые особенности»).

Жёсткие и мягкие модели

Гармонический осциллятор — пример так называемой «жёсткой» модели. Она получена в результате сильной идеализации реальной физической системы. Для решения вопроса о её применимости необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Иными словами, нужно исследовать «мягкую» модель, получающуюся малым возмущением «жёсткой». Она может задаваться, например, следующим уравнением:

Здесь — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения, — некоторый малый параметр. Явный вид функции f нас в данный момент не интересует. Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований. Например, решением уравнения гармонического осциллятора являются функции вида , то есть колебания с постоянной амплитудой. Следует ли из этого, что реальный осциллятор будет бесконечно долго колебаться с постоянной амплитудой? Нет, поскольку рассматривая систему со сколь угодно малым трением (всегда присутствующим в реальной системе), мы получим затухающие колебания. Поведение системы качественно изменилось.

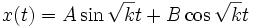
Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы. [20] Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.

Универсальность моделей

Прямая и обратная задачи математического моделирования

Существует множество задач, связанных с математическим моделированием. Во-первых, надо придумать основную схему моделируемого объекта, воспроизвести его в рамках идеализаций данной науки. Так, вагон поезда превращается в систему пластин и более сложных тел из разных материалов, каждый материал задается как его стандартная механическая идеализация (плотность, модули упругости, стандартные прочностные характеристики), после чего составляются уравнения, по дороге какие-то детали отбрасываются, как несущественные, производятся расчёты, сравниваются с измерениями, модель уточняется, и так далее. Однако для разработки технологий математического моделирования полезно разобрать этот процесс на основные составные элементы.

Традиционно выделяют два основных класса задач, связанных с математическими моделями: прямые и обратные.

В простейшем случае (одно уравнение осциллятора, например) прямая задача очень проста и сводится к явному решению этого уравнения.

Обратная задача: известно множество возможных моделей, надо выбрать конкретную модель на основании дополнительных данных об объекте. Чаще всего, структура модели известна, и необходимо определить некоторые неизвестные параметры. Дополнительная информация может состоять в дополнительных эмпирических данных, или в требованиях к объекту (задача проектирования). Дополнительные данные могут поступать независимо от процесса решения обратной задачи (пассивное наблюдение) или быть результатом специально планируемого в ходе решения экперимента (активное наблюдение).

Одним из первых примеров виртуозного решения обратной задачи с максимально полным использованием доступных данных был построенный И. Ньютоном метод восстановления сил трения по наблюдаемым затухающим колебаниям.

Дополнительные примеры

Модель Мальтуса

Скорость роста пропорциональна текущему размеру популяции. Она описывается дифференциальным уравнением

Система хищник-жертва

Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерра — Лотки ответа не дает: здесь требуются дополнительные исследования.

Источник