Математические пирамида что это
Числовые пирамиды
Летим на экскурсию в пустыню, чтобы разгадать математические загадки пирамид! Два числа сложили и записали сумму над ними. Заполни пропуски в пирамиде. Числовые пирамиды
А теперь давайте подробно разберем данное задание.
Рассмотрим следующую ячейку в пирамиде.
Нам известно, что 11 — это сумма 7 и еще одного неизвестного числа. Очевидно, что второе число это 4, таким образом можем заполнить ячейку справа в первом ряду.
Далее найдем число, которое нужно записать во второй ряд пирамиды. Это должно быть число, сложив которое с 11, получилось бы 23. Это число 23 — 11 = 12. Запишем его в пирамиду.
В пирамиде осталось одна пустая ячейка. В ней должно быть число, прибавив к которому 7 должно получиться 12. Т.о. в пустой ячейке слева в первом ряду должно быть число 5.
Далее перейдем ко второй пирамиде.
Рассмотрим ячейки во втором ряду. Там должны два числа в сумма которых должна быть равна 24. При этом, заметим, что чтобы получить искомые два числа во втором столбце, нужно к какому-то неизвестному числу, которое располагается в средней ячейке первого ряда прибавить 3 и 5, то есть разность этих двух чисел должна равняться 2. Под эти условия подходит числа 11 и 13, ведь 11 + 13 = 24, а с другой стороны 13 — 11 = 2. Таким образом, можем заполнить ячейки 2 ряда.
И осталось найди последнее число в первом ряду. Это число можно получить, если его прибавить к 3 и получим тогда 11. Таким образом. это число 8.
Рассмотрим еще несколько числовых пирамид.
Числовые пирамиды — 2 класс
Два числа сложили и записали суммы над ними. Заполни пропуски в пирамидах.
Числовые пирамиды — 2 класс
Заполним пропуске в каждой пирамиде и получим следующие.
Числовые пирамиды — 2 класс — ответ
Числовые пирамиды — 3 класс
Два числа сложили и записали суммы над ними. Заполни пропуски в пирамидах.
Числовые пирамиды — 3 класс
Заполним пропуске в каждой пирамиде и получим следующие.
Числовые пирамиды — 3 класс — ответ
Числовые пирамиды — 4 класс
Два числа сложили и записали суммы над ними. Заполни пропуски в пирамидах.
Числовые пирамиды — 4 класс
Заполним пропуске в каждой пирамиде и получим следующие.
Числовые пирамиды — 4 класс — ответ
Что такое пирамида: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение пирамиды
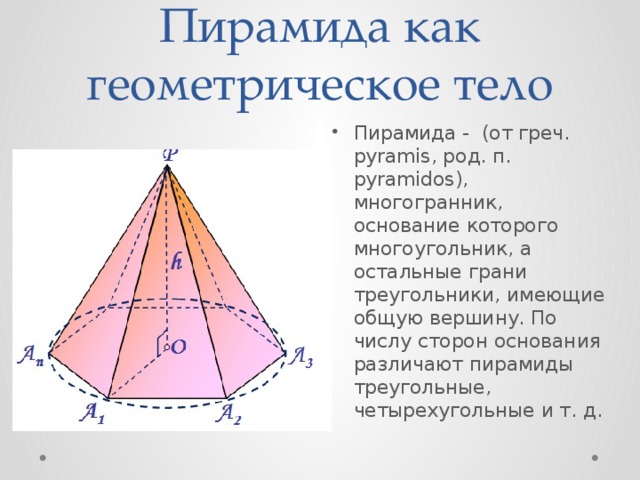
Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.
Примечание: пирамида – это частный случай конуса.
Элементы пирамиды
Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.
Примечание: свойства пирамиды представлены в отдельной публикации.
Виды сечения пирамиды
1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.
Примечание: Существуют и другие виды сечения, но они не так распространены.
Пирамида
Пирамида
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей :
В зависимости от многоугольника, лежащего в основании, пирамиды могут быть треугольными, четырехугольными и т.д.
У треугольной пирамиды есть еще одно название – тетраэдр (четырехгранник).
Формулы вычисления объема и площади поверхности произвольной пирамиды.
Чтобы были понятны формулы, введем обозначения:
В произвольной пирамиде боковые грани могут быть разными треугольниками, поэтому площадь боковой поверхности равна сумме площадей всех боковых граней, найденных по отдельности.
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник
В основании лежит четырехугольник
Прямоугольник
Трапеция
Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее высота приходит в центр основания (в центр описанной окружности). Все боковые ребра правильной пирамиды равны, следовательно, все боковые грани являются равнобедренными треугольниками.
Формулы вычисления объема и площади поверхности правильной пирамиды.
$h_a$- высота боковой грани (апофема)
В основании лежат правильные многоугольники, рассмотрим их площади:
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Объем пирамиды равен трети произведения площади основания на высоту:
Так как пирамида правильная, то в основании у нее лежит равносторонний треугольник, найдем его площадь по формуле:
Подставим все данные в формулу объема и вычислим его:
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
Проектная работа «Математические загадки пирамид»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
[приложение 1] В природе существует много такого, что не может быть ни достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело и надежно использовано на практике без помощи вмешательства математики.
Несмотря на то, что о Великих пирамидах уже многое сказано, нас заинтересовал тот факт, что пирамида – это источник информации о знаниях человека и с ними связано много загадок в разных областях наук. Мы решили провести исследование в попытке разгадать загадку Великих пирамид.
Путешествие во времени приведет нас к корням цивилизации. Теперь мы понимаем, что это очень щекотливая тема, и что сами того не ведая, упрямо держимся за то, что считаем истиной. Но стоит на время забыть привычные представления, чтобы увидеть, как собираются кусочки мозаики, открывая перед нами Великую картину прошлого.
[приложение 2] Цель моего исследования: выявить особенности пирамид с точки зрения математической науки; рассмотреть пирамиды как источник информации.
[приложение 3] Глава 1. Историческая информация о пирамидах
[приложение 4] Пирамиды — величайшие архитектурные памятники, среди которых одно из «семи чудес света» — египетская пирамида Хеопса и почётный кандидат «новых семи чудес света» — Пирамиды Гизы.
[приложение 5] Пирамиды представляют каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта.
Первоначальная высота пирамиды фараона Хеопса в Гизе – 147 м. Это самая большая из древнеегипетских пирамид, и вплоть до 19 в. – самое высокое из рукотворных сооружений.
[приложение 6] Известный нам Джон Рескин говорил: «Искусство – это то, что бесполезно. Как только вещь становится полезной, она более не может быть красивой».
Англичанина Рескина поддерживал француз Теофил Готье: «По-настоящему прекрасным является только то, что ничему не служит». По-видимому, те же взгляды на соотношение пользы и красоты имели и фараоны Древнего царства, жившие за 4500 лет до Рескина и Готье.
Прочность пирамиды недосягаема. Желая прославить своего фараона в веках, древнегреческие зодчие из всех геометрических тел выбрали именно пирамиду. Выбор этот не случаен, ибо в условиях земного тяготения пирамида является наиболее устойчивой конструкцией, способной существовать в веках, без риска обвалиться или рассыпаться.
Главное правило устойчивости конструкции – уменьшение её массы по мере увеличения высоты над землёй – выражено в пирамиде с предельной ясностью и симметрией. Рациональная «полезность» геометрической формы пирамиды заставляют забыть о её утилитарной бесполезности. Именно эта геометрически оправданная форма пирамиды, подчёркнутая её циклопическими размерами и точной системой пропорций, придаёт пирамиде ни с чем не сравнимую выразительность, особую красоту и величие, вызывает ощущение вечности, бессмертия, мудрости и покоя.
Пирамиды продолжают бесстрастно взирать на проходящих у их подножия людей, прославляя в веках мудрость, мастерство и вдохновение древнеегипетских зодчих.
Исчезнут в веках города,
Разрушатся стены и своды,
Пройдут племена и народы;
Но будет звучать наш завет
Сквозь сонмы мятущихся лет!
Что в нас, то навек неизменно.
Песнь лиры, созданье резца.
Но будем стоять до конца.
Как истина под покрывалом Изиды,
[приложение 9] Глава 2. Математические загадки пирамид
2.1. Архитектурные теории
Конструкция древнеегипетской пирамиды является самой простой, прочной и устойчивой. Вес каждого верхнего блока пирамиды по всей поверхности передаётся нижним блокам. Форма пирамиды представляет полное единство с её конструкцией. Однако такая конструкция не создаёт внутреннего объёма и, по существу, не является архитектурной конструкцией.
Интересно, как же строились эти огромные памятники?
Перечислим 8 основных этапов строительства великих пирамид, которые легли в основу нашего исследования.
Перед возведением пирамиды строители сравняли с землёй небольшое возвышение и установили в середине гигантскую ось. Вокруг этой оси было вырезано 6000 гектаров горной породы под блоки странной формы, каждый из которых по массе приближается к легковому автомобилю.
строители транспортировали 130 гранитных блоков более чем на 800 километров.
Каждый блок весит от 12 до 70 тонн. Затем эти блоки необходимо было поднять на 65 метров, что не просто сделать и сейчас.
в Пирамиде Хеопса всего 3 внутренних помещения, ничтожно малых по сравнению с величиной монумента.
Это нижняя, средняя и верхняя камеры.
Каменщики построили проход длиной около 90 метров, шириной менее метра.
[приложение 13] Этот проход, ведущий в нижнюю камеру, пробит прямо в скале.
[приложение 14] Архитектор Пьер Луиджи Копат удивлен этой конструкцией:
«В таком узком проеме условия для работы должны были быть просто ужасающими. Также для того, чтобы угол наклона прохода оставался точным и постоянным, требовалось использование специальных инструментов. Эти инструменты должны были позволять сохранять этот угол во время всего процесса работы».
Пирамида составлена из более чем 2 миллионов блоков, разной формы и величины, хотя проще работать с блоками одинаковой величины. Каждый блок примерно весит как легковой автомобиль. А точность общей конструкции соответствует современным стандартам.
Верхняя камера идеально выровнена в горизонтальных и вертикальных плоскостях. Точность превышает стандарты современного строительства. Несмотря на то, что погрешность в 8 миллиметров осталась бы незамеченной, она едва отклоняется на пол миллиметра.
Пирамида Хеопса пережила как минимум 3 масштабных землетрясения, последнее из которых сравнял с землей Каир в тринадцатом веке.
Географическая ориентация пирамиды практически безукоризненна. Она указывает на север с отклонением в 5 сотых градуса. Подобной точности попытались снова достичь лишь в 17 веке. Но тогда удалось добиться в пять раз менее точной ориентации.
Время построения пирамиды Хеопса должно было составить 20 лет. Быстрый подсчёт даёт нам примерную оценку скорости процесса строительства.
При рабочей смене в 12 часов, учитывая, что в году 365 дней, а каменных блоков более 2 миллионов, то один блок должен был добываться, вырезаться, подниматься и устанавливаться за 2,5 минуты.
Строители пирамиды жили до изобретения железа и стали. Возведение единственного из Чудес Света, дошедшего до наших дней, происходило с помощью медных стамесок, каменных молотков, веревки и большой смекалки.
[приложение 20] Подведем итог:
Около 47 веков назад, когда б о льшая часть человечества бродила по планете в звериных шкурах, каменщики строили Великую пирамиду Хеопса в Гизе.
Одна известковая возвышенность сравнена с землёй.
Шесть тысяч гектаров породы использованы для мощения, что эквивалентно шести футбольных полям.
Установлено более 2 млн блоков, общая масса которых превышает 6 млн тонн – высота 42-этажного здания.
Узкий, точно спланированный 90-метровый проход, пробитый прямо в камне и идущий сквозь всю пирамиду.
130 гранитных блоков, поднятых на 65 метров с погрешностью в полмиллиметра.
8 сторон вместо четырёх.
Точность постройки на современном уровне.
Географическая ориентация на современном уровне.
И всё это – за 20 лет работы с применением этих инструментов.
Обратимся к двум современным проектам, которые помогут увидеть размах строительства пирамиды.
[приложение 22] В 60-х года прошлого века 22 страны с помощью передовых технологий подняли храм Абу-Симбел, чтобы предотвратить его затопление водой из Асуанской дамбы. Несмотря на наличие кранов и грузовиков, у строителей ушло 5 лет на перестройку этого храма, состоящего из 2200 каменных блоков, самый тяжёлый из которых весил 30 тонн.
[приложение 24] Задача стала бы проще, если бы период постройки был бы и дольше. Строительство пирамиды Солнца в Мексике, высота которой в 2 раза меньше пирамиды Хеопса, длилась 150 лет.
Почему египтологи продолжают придерживаться странной версии о 20 годах строительства? Потому что если они примут срок, превышающий период правления Хеопса, вся теория о роли пирамиды в качестве гробницы рухнет, а это недопустимо.
[приложение 25] Мы изучили другие строения, такие же древние как пирамида, а также еще более древние постройки. Здесь мы нашли бесценные подсказки. Везде мы увидели блоки странной формы.
[приложение 26] Но потом мы узнали это: структура закладки камня передается в зеркальном отображении на другую сторону прохода.
[приложение 27] Жозеф Давидович, геохимик и египтолог говорил: «Если вы хотите чтобы ваш монумент стоял долго, его структура должна быть разнородной. Это предотвратит обрушение стен в случае нагрузок, например, при землетрясении».
[приложение 28] Вспомним, что у пирамиды 8 граней, хотя четырехгранную пирамиду построить гораздо легче. А лишние грани кажутся бесполезными, но это не так: для этого мы отправимся в довоенный Каир.
[приложение 30] 2.2. Геометрические факты
Египетские пирамиды являют собой удивительный пример геометрической и математической мистики. Великая пирамида имеет квадратное основание (в настоящее время длины сторон равняются: северная — 230,25 м, южная — 230,4, восточная — 230,38, западная — 230,35 м.)
Периметр постройки — примерно 1 км.
Площадь основания пирамиды —54 тысячи м2.
Объем всего сооружения — более 2 500 000 м3.
Для сравнения: в нем свободно может разместиться любой из европейских храмов, а из камня, использованного в пирамиде можно построить все известные храмы Европы. Во всех деталях Великой пирамиды сохранены совершенные (золотые) пропорции.
[приложение 31] Основание пирамиды – квадрат.
[приложение 32] А меняя высоту этой точки, мы можем построить любую пирамиду с квадратной базой.
[приложение 33] Для построения Великой пирамиды нужен был круг, длина которого была бы равна периметру квадрата.
[приложение 34] И если мы поднимем половину круга, мы получим точную высоту Великой пирамиды.
Только пользуясь такой сложной математической схемой, можно было найти число Пи и «золотое число».
Больше всего удивляет то, что высочайшую точность в проекте и его реализации смогли заметить только с применением современного оборудования.
[приложение 35] 2.3. Астрономические факты
Известно, что если провести горизонтальную линию через центр Земли до пересечения с ее окружностью, потом начертить линии из точек пересечения вверх к центру Луны, а из центра Луны обратно на Землю, то это будут точные пропорции Великой пирамиды.
Египтологи из значений высоты и длины основания Великой пирамиды выводят множество космологических закономерностей и параметров, основными из которых являются:
3,4 — длина витка спирали ДНК для всех живых существ;
3:40 — отношение площадей поверхностей Земли;
1:49 — соотношение объемов Луны и Земли;
1:81,3 — соотношение масс Луны и Земли;
499 (секунд) — время, за которое солнечный свет проходит расстояние до Земли.
Длина стороны основания, выраженная не в метрах, а в египетских локтях, точно соответствует продолжительности земного года — 365 дней.
[приложение 36] Заключение
О чудесах пирамид сейчас не рассуждают только ленивые: в них практически нет бактерий, говорят, туда поступает космическая энергия и складывается уникальный микроклимат, что связано с формой сооружения. Из научных фактов: в пирамиде существуют места, где биологические продукты сохраняются неограниченное время. Есть в Пирамидах также области, где у человека возникают состояния, стимулирующие его творческую активность, раскрывающие интуицию.
Взглянув на это с точки зрения геометрии, мы можем подойти к пониманию вопроса, описав его очень простым приемом. Согласно теории гармонического резонанса, пирамида является резонатором и генератором, и структура пирамиды может оказывать на человека корректирующее действие. То, что пирамиды правильного сечения благотворно воздействуют на клетки, омолаживая организм и избавляя его от болезней, научный факт, хотя и не имеет объяснения.
По-видимому, по замыслу проектировщиков, Пирамида создавалась как инструмент для воздействия на психофизическую структуру человека. Причем множества людей. Пирамида интересна тем, что в ее конфигурации имеют место не вертикальные плоскости, как в обычной архитектуре, а именно наклонные.
Египетские пирамиды не только древние памятники архитектуры, но и хранилища тайн, закономерностей, научных загадок. Многое в них необъяснимо, но все это интересно современным археологам и историкам.
По результатам нашей работы можно утверждать, что свойства пирамид уникальны.
В ходе выполнения работы я приобрела навыки работы с большим объемом информации, раскрыла тонкости свойств пирамиды, думаю, что полученные знания пригодятся в жизни.
Мне интересны загадки, непонятные истории, связи многих наук в одном объекте, исторические тайны. Именно поэтому я выбрала эту тему для своего исследования.
1. А.В. Волошинов. Математика и искусство, М: «Искусство», 1985 г.
2. Г.И. Глейзер. История математики в школе, М: «Просвещение», 1982 г.
3. И. Исупова. Всё обо всём Т.8, М: «Слово», 1997 г.
4. И.Ф. Шарыгин. Геометрия 10-11 класс, М: «Просвещение», 2000 г.
5. Б. Риен. Ст. «Магический кристалл», «Аномалии» №2 1998 г.
6. К. Гридин. Ст. «Искать ответы никогда не поздно», «Загадки Земли» №2 1999 г.
7. А. Богдановский. Ст. «Прогнозы Сергея Проскурякова подсказаны строителями пирамид», «Комок» №6 1998 г.
8. Питер Томпкинс «Тайны великой пирамиды Хеопса», М: «Центрополиграф»,2005 г.
«Секреты математических пирамид»
Актуальность выбранной темы
•Пирамида как геометрическая форма — пожалуй, одно из самых совершенных в природе. Изучением пирамид занимались многие археологи, ученые, математики и каждый из них открывал новые свойства этих сооружений. По сей день существует еще много загадок, связанных с пирамидами. Интерес к этому геометрическому телу никогда не пропадет.
Просмотр содержимого документа
«»Секреты математических пирамид» »
МКОУ «Михайлоанненская средняя общеобразовательная школа»
Проект по математике
«Секреты математических пирамид»
Автор проекта: Буланова Наталья,
Секреты математических пирамид
Актуальность выбранной темы
Этапы подготовки проекта:
Тема проектной работы:
Секреты математических пирамид
Цели и задачи проекта
С давних времен пирамиды как геометрические тела привлекают внимание специалистов разных профилей. Представляют интерес для историков, археологов, физиков, биологов, медиков, философов. Чем больше мы узнаем о пирамидах, тем больше у нас возникает вопросов. На некоторые из них, наверное, уже невозможно получить однозначного ответа, но не стоит забывать и о том, что пирамиды таят в себе ответы на огромное количество вопросов, которыми сейчас задается наука. Один из таких вопросов зависимость свойств пирамидальных предметов от их форм и пропорций.
В своем проекте я решила ответить на этот вопрос, используя самые разнообразные исследования ученых мира.
Пирамида как геометрическое тело
Пирамидальные формы в природе
С чего все началось…
Чудодейственные свойства пирамид
В течении ряда лет экспериментаторы из различных стран (США, Франция, Россия и др.) проводят опыты по использованию пирамид.
Отмечены следующие явления:
Лечебные свойства пирамид
Влияние пирамид на искусство
Занимательная математика египетских пирамид
Пирамиды в архитектуре
Челябинск, пирамида, торговый центр
г. Курск, торговый центр «Европа»
Рига. Курортная зона.
Инициатором строительства пирамид в России является директор московского НПО Гидрометеоприбор Александр Голод. Подмосковная 44-метровая громадина возведенная на 38 километре Новорижского шоссе — семнадцатая из построенных им пирамид и, похоже, далеко не последняя.
Уже существует разработанный им проект построения кольца пирамид вокруг Москвы. Весьма увлекающийся человек, он считает исследование и строительство пирамид своей миссией и, пожалуй, наиболее важным делом своей жизни.
Список использованной литературы