Математика что такое звенья
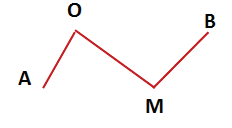
Ломаная линия
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
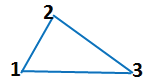
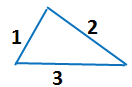
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
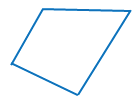
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Поделись с друзьями в социальных сетях:
Математика. 2 класс
Конспект урока
Математика, 2 класс. Урок №13.
Длина ломаной. Закрепление
Перечень вопросов, рассматриваемых в теме:
— Как найти длину ломаной?
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
Длина ломаной – это сумма длин всех её звеньев.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35
Теоретический материал для самостоятельного изучения
На рисунке мы видим ломаную линию, состоящую из трёх звеньев.
Как найти длину ломаной линии? Это можно сделать двумя способами.
Первый способ. Сначала узнаем длину каждого звена с помощью линейки
Длина первого звена 4 см.
Длина второго звена 6 см.
Длина третьего звена 5 см.
Найдем сумму этих длин.
Найдем длину ломаной вторым способом.
Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.
Накладываем циркуль на второй отрезок, переносим его на прямую.
Накладываем циркуль на третий отрезок, переносим его на прямую.
Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.
Выводы: длину ломаной можно находить двумя способами.
Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.
Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка. Это и будет длина всей ломаной.
1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см
2. Расположите ломаные линии по порядку: от самой короткой до самой длинной
Правильный вариант: Найдем длину каждой ломаной
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Ломаная линия
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
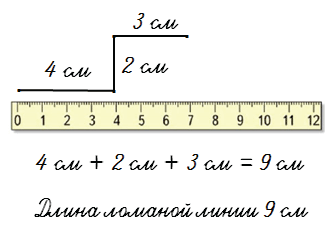
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
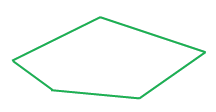
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Многоугольники
Ломаная — это геометрическая фигура, которая состоит из точек,
соединенных отрезками. Отрезки называются звеньями ломаной,
а точки называются вершинами ломаной. Сумма длин всех
звеньев называется длиной ломаной.
Замкнутая ломаная — это ломаная, у которой конец последнего
звена совпадает с началом первого звена.
Простая ломаная — это ломаная, у которой нет пересечений.
Многоугольник — это геометрическая фигура с множеством
углов и сторон, или по другому это простая замкнутая ломаная,
у которой соседние звенья не лежат на одной прямой.
Как и у любой другой геометрической фигуры, у многоугольника
есть стороны и углы. Звенья ломаной называют сторонами
многоугольника, а вершины ломаной называют углами
многоугольника. Периметр многоугольника равен сумме
длин всех сторон многоугольника, или по другому длине ломаной.
Соседние вершины многоугольника — это два угла
многоугольника,принадлежащие одной стороне.
Диагональ многоугольника — это отрезок, соединяющий
две любые не соседних угла.
Произвольный многоугольник разделяет плоскость на две части.
Одна из частей называется внутренней областью, а другая внешней
областью многоугольника. Углы, которые находятся во внутренней
области называются внутренними, соответственно углы, которые
находятся во внешней области называются внешними.