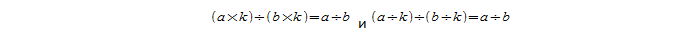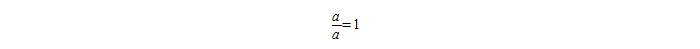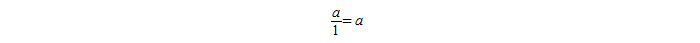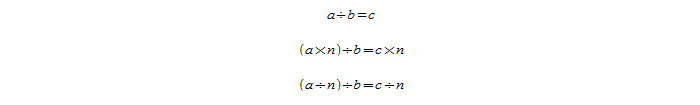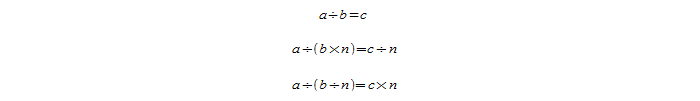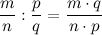Математика что значит частное
Что такое частное в математике?
В каждом разделе научных или практических знаний используются собственные понятия и определения. Они нужны человеку для того, чтобы максимально упростить понимание и применение разных явлений и действий, которые описываются при помощи этих терминов. «Частное» является таким термином, этим словом описывают одну из четырёх простейших операций в математике.
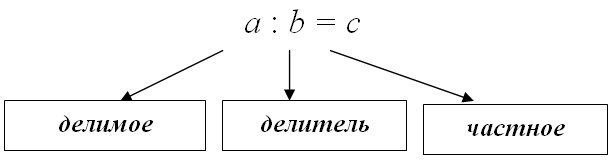
В математической операции деления участвуют несколько чисел, каждому из них присвоено определённое название. «Частным» называют результат деления, другие задействованные в этой операции компоненты обозначают как «делимое» (число, на которое делят), «делитель» (количество единиц деления) и «остаток» (представляет собой произведение дробной части частного на делитель). К примеру, при целочисленном делении числа 34 на 6 к частному будет относиться 5, к делимому – 34, к делителю – 6, а остатком от деления будет являться число 4.
Если в операции присутствует одна или несколько переменных, то частное не всегда будет представлять из себя целое или дробное число, это может быть и просто математическое выражение. В целом, к частному можно отнести всё, что находится после знака равенства в тождестве, где левая часть – это операция деления. К примеру, в случае деления выражения 6*x?+12 на 3, частным будет являться выражение 2*x?+4.
Иногда термин «частное» заменяют обозначением «отношение». Т.е., теоретически, назвав результат деления 34 на 6 любым из данных двух определений, вы будете в обоих случаях правы. Однако всё-таки чаще всего термином «отношение» называют левую часть тождества, иначе говоря, ещё не осуществленную операцию деления, а термин «частное» применяют к правой части, т. е. к полученному результату.
Слово «частное» применяют не только в качестве математического термина, существуют и другие широко используемые понятия, обозначаемые точно также. Нередко это слово употребляют в виде прилагательного для подчёркивания противопоставления – к примеру, «частное мнение». В области юриспруденции слово «частное», по сути, аналогично понятию «негосударственное» – к примеру, «частная собственность».
Вместе со статьёй «Что такое частное в математике?» читают:
Частное в математике — определение, свойства и формула
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Что такое частное чисел в математике
Определение частного чисел (деление)
Частное чисел — это результат получаемый при определении количества содержания одного числа в другом. Проще говоря это обычное деление. При этом общепринятые оперируемые понятия для частного это делимое, делитель и само частное — результат.
Пример. Найти частное чисел:
Ответ: 20:2=10 и 35:7=5.
Это был самый простой пример. Все самое интересное впереди! Проблемы с делением начинаются тогда, когда числа становятся большими и выходят за рамки таблицы умножения. Здесь приходится делить большое число по определенному правилу. Такое деление еще называется деление в столбик.
Пример. Найти частное чисел:
-894| 3__ 6 | 298-29 27— 24 24 0
Видео
Общая информация
Частное — это значит, что что-то принадлежит одному человеку или же относительно небольшой группе людей. Причем они объединены на добровольной основе, а не в приказном порядке (как пример можно в последнем случае привести коммунальные предприятия). А это, в свою очередь, обозначает определённую специфику. Также, когда говорят про частное, это может означать отдельный, весьма редкий или вообще единичный случай чего-то. Кроме этого, так называется одноименный математический оператор.
Как видите, слово «частное» — это весьма широко используемый инструмент нашего языка. Чтобы лучше понять его использование, давайте рассмотрим его применение на практике. Для полноты обзора будет уделено внимание и общему примеру, и частному. Итак, приступим.
Наглядные примеры
Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.
Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:
Запишем простой пример из математики:
80:2=40
80 – делимое (оно делится)
2 – это делитель (на него разделяют)
Восемьдесят больше, чем сорок, в два раза.
Другой пример выглядит так:
120:2=60
Сто двадцать больше, чем шестьдесят, в два раза.
Деление
В математике есть четыре простейших операции:
Если мы говорим о частном, то нас будет интересовать такая операция, как деление.
В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.
Частное рассказывает, во сколько раз одно число больше другого.
Правило деления целых чисел
Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.
Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:
Плюс на плюс дает плюс. “+ : + = +”
Минус на минус дает плюс. “– : – =+”
Минус на плюс дает минус. “– : + = –”
Плюс на минус дает минус. “+ : – = –”
А теперь рассмотрим подробно каждый пункт правила деления целых чисел.
Деление целых чисел с разными знаками. Правило и примеры
При выполнении деления целых чисел с разными знаками, частное будет равно отрицательному числу.
Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.
Минус на плюс дает минус. Плюс на минус дает минус.
Пример: Вычислите деление 4716:(-524).
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Математика что значит частное
Что такое частное чисел (онлайн калькулятор на деление)
Определение частного чисел (деление)
Это был самый простой пример. Все самое интересное впереди! Проблемы с делением начинаются тогда, когда числа становятся большими и выходят за рамки таблицы умножения. Здесь приходится делить большое число по определенному правилу. Такое деление еще называется деление в столбик.
Как делить столбиком (о правилах деления столбиком)
4. Если в конце таких вычислений получается число которое невозможно поделить на делитель и сносить уже нечего, то это было деление с остатком. То есть оставшееся число или цифра, это остаток. Надо понимать, что остаток всегда должен быть меньше делителя. В этом вся соль остатка, он не позволяет взять из себя делитель даже одного раза!
Деление рациональных дробей
Для деления дробей используется следующее правило.
То есть если сказать без глубоких объяснений процессов происходящего, берем дробь, где в числителе произведение числителя делимого и знаменателя делителя, а в знаменателе этой дроби произведение знаменателя делимого и числителя делителя!
Что же, я думаю вы уже утомились воспринимать информацию и теперь вам лучше всего развеяться, поиграв с онлайн калькулятором на деление. А и тут сразу же в голове всплыло еще одно правило, на ноль делить нельзя, так как даже в самом маленьком числе нулей великое множество, то есть бесконечность, а наш курс все же для школьников начальных и средних классов, где о бесконечности знают лишь то, что можно бесконечно играть в компьютер и не более:) А как на деление с нолем отреагирует калькулятор, можете проверить сами.
Побалуемся с делением!?
Цифра которую будем делить (делимое)