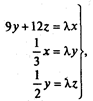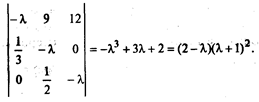Матричные модели отличаются тем что они

Матричные модели отличаются тем что они

Модели данного класса регулярно строятся во многих странах мира. С их помощью решаются задачи анализа, планирования и прогнозирования развития экономических систем. Задачи, в решении которых могут быть применены матричные модели:

· регулирование экономического развития;

· расчеты по составлению долгосрочных планов;

· расчеты по оптимизации внешней торговли;

· составление межрегиональных балансов;

· расчеты по ценообразованию и т.д.

Типичным примером матричных моделей считается экономико-математическая модель межотраслевого баланса (модель В.В. Леонтьева). За разработку и применение этого метода к решению важных экономических проблем в 1973 году Василий Васильевич Леонтьев был удостоен Нобелевской премии в области экономики.

В западной литературе модели данного класса именуются как метод «затраты-выпуск».

ОБЩАЯ СТРУКТУРА МЕЖОТРАСЛЕВОГО БАЛАНСА

Центральным элементом матричных моделей является межотраслевой баланс. Он представляет собой таблицу, характеризующую связи между различными отраслями экономики страны.

Производственная сфера экономики представлена в балансе в виде совокупности n отраслей. Баланс состоит из четырех разделов (квадрантов).

Первый квадрант представляет собой матрицу, состоящую из (n+1) строки и (n+1) столбца. Этот раздел является важнейшей частью баланса, поскольку именно здесь содержится информация о межотраслевых связях.

В зависимости от того, в каких единицах измеряются потоки продукции в балансе, существуют различные его варианты:

· в натуральном выражении;

· в денежном (стоимостном) выражении,

· в трудовых измерителях.

Рассмотрим баланс в стоимостном выражении, в котором потоки продукции измеряются на основе стоимости произведенной продукции в некоторых фиксированных ценах. Поскольку в этом случае величины x_ij отражают стоимость продукции, т.е. измеряются в одних и тех же единицах, их можно просуммировать.

Сумма по строке представляет собой сумму всех поставок i—й отрасли другим отраслям.

Сумма по столбцу характеризует производственные затраты j-й отрасли на приобретение продукции других отраслей.

На пересечении (n+1)-й строки и (n+1)-го столбца находится промежуточный продукт экономики

Второй раздел посвящен конечному продукту.

В конечную продукцию, как правило, включаются:

· возмещение выбытия основных средств;

· личное потребление населения;

· расходы на содержание государственного аппарата;

· а также сальдо экспорта и импорта.

Ко второму разделу относится также столбец валовых выпусков (X_i). В пределах первого и второго разделов справедливо соотношение:

Третий квадрант межотраслевого баланса отражает стоимостную структуру валового продукта отраслей. В (n+2)-й строке таблицы отражена условно чистая продукция (V_j), представляющая собой разницу между величиной валовой продукции отрасли и суммарными затратами отрасли:

Важнейшими составляющими чистой продукции отрасли являются заработная плата, прибыль и налоги. Можно показать, что суммарный конечный продукт равен суммарной условно чистой продукции

Таким образом, в третьем разделе также фигурирует конечный продукт, но если во втором разделе он разбивается на величины y_i, характеризующие структуру потребления, то в третьем разделе величины V_j показывают, в каких отраслях произведена стоимость конечного продукта.

Четвертый раздел располагается под вторым.

Он характеризует перераспределения в экономике, осуществляемые через финансово-кредитную систему. В плановых расчетах четвертый раздел, как правило, не используется, и поэтому здесь рассматриваться не будет.

Он строится на основе агрегирования результатов деятельности отдельных предприятий. Такой баланс называют отчетным. Кроме этого строятся плановые балансы, предназначенные для разработки сбалансированных планов развития экономики.

n СТАТИЧЕСКАЯ МЕЖОТРАСЛЕВАЯ МОДЕЛЬ

Статические межотраслевые модели используются для разработки планов выпуска и потребления продукции и основываются на соотношениях межотраслевого баланса.

При построении модели делают следующие предположения:

1) все продукты, производимые одной отраслью, однородны и рассматриваются как единое целое, т.е. предполагается, что каждая отрасль производит один продукт ;

2) в каждой отрасли имеется единственная технология производства ;

3) нормы производственных затрат не зависят от объёма выпускаемой продукции ;

4) не допускается замещение одного сырья другим.

В действительности эти предположения не выполняются. Даже на отдельном предприятии обычно: выпускаются различные виды продукции, используются различные технологии, удельные затраты зависят от объема выпуска и допускается замена одного сырья другим. Следовательно, эти предположения тем более неверны для отрасли. Однако такие модели получили широкое распространение и, как показала практика, они вполне адекватны и применимы для составления планов выпуска продукции. При этих предположениях величина x_ij может быть представлена следующим образом:

МАТРИЦА КОЭФФИЦИЕНТОВ ПРЯМЫХ МАТЕРИАЛЬНЫХ ЗАТРАТ

Подставляя выражение (3) в формулу (1), получим (4)

Можно записать в матричном виде

Их значения могут быть получены двумя путями:

1) статистически : коэффициенты определяются на основе анализа отчётных балансов за прошлые годы.

2) нормативно : предполагается, что отрасль состоит из отдельных производств, для которых уже разработаны нормативы затрат, на их основе рассчитываются среднеотраслевые коэффициенты. Выражение (4) принято называть балансом распределения продукции. Его можно использовать для анализа и планирования структуры экономики. Если известны коэффициенты прямых материальных затрат, то, задав конечный продукт по каждой отрасли, можно определить необходимые валовые выпуски отраслей. В этом заложена основная идея использования матричных моделей для планирования производства.

Преобразуем выражение (4):

До начала планирования следует выяснить, существует ли матрица, обратная матрице (E-A), и не будут ли получены отрицательные значения выпуска по отраслям. Установим некоторые свойства коэффициентов прямых материальных затрат:

Для любой отрасли условно чистая продукция есть величина положительная, поскольку включает в себя заработную плату, амортизацию, прибыль и т.д., т.е. V_j>0. Поэтому, используя соотношение (2), можно записать:

Можно показать, что

Из соотношения (7) следует b_ij ≥ a_ij, таким образом, коэффициент полных материальных затрат b_ij, описывающий потребность в выпуске продукции i-й отрасли в расчете на единицу конечного продукта j-й отрасли, не меньше коэффициента прямых материальных затрат a_ij, рассчитываемого на единицу валового выпуска. Кроме того, из соотношения (7) для диагональных элементов матрицы B следует: b_ii ≥ 1, взаимосвязь коэффициентов прямых и полных материальных затрат проследим на примере.

Пусть единицей выпуска хлебопекарной промышленности является хлеб. Взаимосвязь коэффициентов прямых и полных материальных затрат.

Полные затраты электроэнергии для нашего примера складываются из прямых затрат и косвенных затрат всех уровней. Косвенные затраты высоких уровней являются незначительными и при практических расчетах ими можно пренебречь.

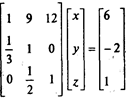
Пример : Даны коэффициенты прямых затрат a_ij и конечный продукт Y для трехотраслевой экономики

a) коэффициенты полных затрат;

b) вектор валового продукта;

c) межотраслевые поставки продукции;

d) проверить продуктивность матрицы А;

e) заполнить схему межотраслевого баланса.

Для решения использовать функции Excel

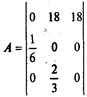
Далее вычисляем матрицу коэффициентов полных затрат В-(Е-А).

Для вычисления матрицы В:

a. Выделить диапазон ячеек для размещения матрицы

b. Выбрать функцию МОБР в категории математические

c. Ввести диапазон ячеек, где содержится Е-А

d. Нажать клавиши CTRL+SHIFT+ENTER

Все элементы матрицы В неотрицательны, следовательно матрица А продуктивна. Вычислим вектор валового выпуска Х по формуле X = BY

Для умножения матриц необходимо:

a. Выделить диапазон ячеек для размещения результата умножения матриц

b. Выбрать функцию МУМНОЖ в категории математические

Нажать клавиши CTRL+SHIFT+ENTER

1. Области применения матричных моделей?

2. Структура межотраслевого баланса?

3. Связь между конечной и условно чистой продукцией?

4. Экономический смысл, свойства и способы расчета коэффициентов прямых материальных затрат?

5. Коэффициенты полных материальных затрат?

6. Экономический смысл коэффициентов прямых затрат труда.?

Источник

Матричные модели

Матричные модели [matrix models] — экономико-математические модели, построенные в виде таблиц (матриц). Они отображают соотношения между затратами на производство и его результатами, нормативы затрат, производственную и экономическую структуру хозяйства. Применяются в межотраслевом балансе, матричном промфинплане предприятия, при решении отраслевых задач оптимального планирования развития и размещения производства, в эколого-экономическом моделировании и т.д.

Широкое распространение М.м. связано, в частности, с тем, что запись данных в табличной форме облегчает их введение в компьютер и дает наглядное представление о результатах расчета (на самом деле ввиду большой размерности моделей они обычно не изображаются непосредственно в виде таблиц, а содержащаяся в них информация хранится в памяти компьютера — см. об этом в статье Массив данных). Для перехода между М.м. различных звеньев (уровней хозяйства) применяются вариантные матрицы.

М.м. применяются и в теоретических исследованиях экономики, поскольку она представляется как процесс преобразования затрат в результаты. Элементами матрицы при этом являются величины затрат при разных «технологических способах«. В таких исследованиях часто термин «матрица» отождествляется с термином «экономика». Употребляют, например, в одном и том же смысле термины «продуктивная матрица» и «продуктивная экономика» (см. Продуктивность матрицы).

Полезное

Смотреть что такое «Матричные модели» в других словарях:

МАТРИЧНЫЕ МОДЕЛИ — в экономике балансово нормативные модели в виде таблиц (матриц), отражающие соотношения затрат и результатов производства, нормативы затрат, производственные и экономические структуры. Применяют в межотраслевом балансе, при составлении… … Большой Энциклопедический словарь

матричные модели — Экономико математические модели, построенные в виде таблиц (матриц). Они отображают соотношения между затратами на производство и его результатами, нормативы затрат, производственную и экономическую структуру хозяйства. Применяются в… … Справочник технического переводчика

МАТРИЧНЫЕ МОДЕЛИ — англ. matrix models; нем. Matriocmodelle. В социологии прямоугольные таблицы (матрицы), элементы к рых отражают взаимосвязи свойств соц. объектов, значение к рых определяется в соответствии с правилами теории матриц. Antinazi. Энциклопедия… … Энциклопедия социологии

матричные модели — в экономике, балансово нормативные модели в виде таблиц (матриц), отражающие соотношения затрат и результатов производства, нормативы затрат, производственные и экономические структуры. * * * МАТРИЧНЫЕ МОДЕЛИ МАТРИЧНЫЕ МОДЕЛИ в экономике,… … Энциклопедический словарь

Матричные модели — в экономике, один из наиболее распространённых типов экономико математических моделей. Представляют собой прямоугольные таблицы (матрицы (См. Матрица)), элементы которых отражают взаимосвязи экономических объектов и обладают определённым… … Большая советская энциклопедия

МАТРИЧНЫЕ МОДЕЛИ — англ. matrix models; нем. Matriocmodelle. В социологии прямоугольные таблицы (матрицы), элементы к рых отражают взаимосвязи свойств соц. объектов, значение к рых определяется в соответствии с правилами теории матриц … Толковый словарь по социологии

Матричные модели в экономике — Связать? Матричные модели в экономике представляют собой прямоугольные таблицы (матрицы), в которых отражается: структура затрат на производство и распределение продукции и вновь созданной стоимости … Википедия

МОДЕЛИ ВОСПРОИЗВОДСТВА НАСЕЛЕНИЯ — МОДЕЛИ ВОСПРОИЗВОДСТВА НАСЕЛЕНИЯ, описывают процесс возобновления поколений; класс моделей демографических. Устанавливают связь между числ. и возрастной структурой населения, с одной стороны, и режимом рождаемости и порядком вымирания с другой;… … Демографический энциклопедический словарь

Матричные популяционные модели — Популяционные модели используются в популяционной экологии для моделирования динамики популяций животных или человека. Матричные популяционные модели это особый тип популяционных моделей, использующий матричную алгебру. Матричная алгебра, в свою… … Википедия

Матричный анализ — Матричные модели в экономике Матрица в математике … Википедия

Источник

Матричные модели

Матричную модель можно рассматривать как конечно-разностный аналог динамической модели. Один из ранних вариантов матричной модели был разработан Льюисом и Лесли [30] как детерминистская модель, предсказывающая будущую возрастную структуру популяции самок по известной структуре в настоящий момент времени и гипотетическим коэффициентам выживания и плодовитости. Популяцию разбивают на n+1 возрастную группу (т. е. 0, 1, 2. п, причем каждая группа состоит из особей одного возраста), так что самая старшая группа, или группа, в которой все доживающие до данного возраста животные вымирают, имеет номер п. Обозначая через x_n число особей в каждой возрастной группе, получаем вектор 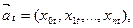представляющий возрастную структуру в момент времени t.

Модель описывается матричным уравнением

(9.19)

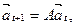
которое запишем в развернутом виде:

где величины f_i,(i=0,1. n) представляют число самок, производимых самкой i-го возраста,

Покажем, что поведение модели можно предсказать, анализируя некоторые формальные свойства матрицы А. Во-первых, последовательно умножая уравнение (9.19) на матрицу А, легко получить более общие уравнения для численности возрастных групп к моменту времени

(9.21)

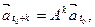
Во-вторых, поскольку матрица А квадратная с (n+1) строками и столбцами, она имеет n+1 собственных чисел (с учетом кратности) и (n+1) собственных (и присоединенных) векторов. Элементы А являются либо положительными числами, либо нулями, поэтому наибольшее (по абсолютной величине) собственное число и координаты отвечающего ему собственного вектора положительны и при этом имеют определенный экологический смысл. Проиллюстрируем это на одной из простейших моделей, предложенных Уильямсоном [54].

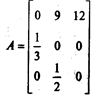
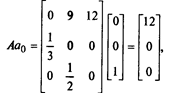
Исходная популяция имеет вектор, представляющий возрастную структуру а₀ = (0,0,1), т. е. популяция состоит из одной самки старшего возраста. Матрица А имеет вид:

По прошествии одного временного интервала имеем

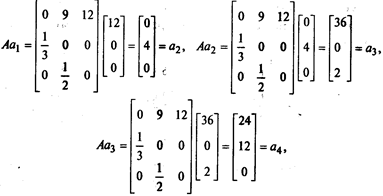
т. е. a₁ = (12, 0, 0) и в популяции уже будет 12 самок младшего возраста. Повторное применение модели дает следующие результаты:

Главное собственное число и собственный вектор матрицы А можно найти известными методами, имея

(9.22)

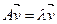
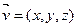
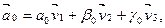
или полагая – систему линейных алгебраических уравнений

(9.26)

где α₀, β₀, γ₀ – некоторые положительные числа (например, если 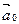= (258, 30, 17), то α₀=10, β₀=3, γ₀=2).

Тогда уравнение (9.21) примет вид:

(9.27)

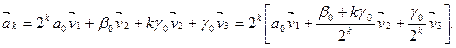
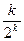
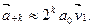
Так как → 0, k → ∞, то при t=+k → ∞популяция возрастает по экспоненциальному закону

(9.28)

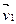
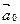
Главное собственное число λ₁ дает скорость, с которой возрастает размер популяции (в нашем примере за каждый временной интервал популяция удваивается), а собственный вектор определяет устойчивую возрастную структуру популяции, т. е. отношение численностей особей разных возрастных групп остается постоянным и равным 24:4:1. Нетрудно видеть, что если мы в конце каждого временного интервала будем изымать половину популяции и использовать на корм, то размер ее станет равным исходному .

Матричные модели очень удобны для расчета на ЭВМ и находят все более широкое применение, например, для анализа круговорота питательных веществ в экосистемах, в различных стохастических моделях [54] (в марковских моделях и т.д.).

1. Показать, что график логистического уравнения имеет единственную точку перегиба. Найти ее и дать биологическую интерпретацию.

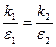
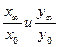
2. Рассмотреть систему Вольтерра в случае . Найти отношения .

3. Построить и исследовать модель эпидемии в городе с 300-тысячным населением.

4. Исходная популяция имеет следующую возрастную структуру a₀ = (0,6,12) и матрица Лесли А – следующий вид:

Найти (приближенно) численность популяции через достаточно большое число п лет и ее устойчивую возрастную структуру.

Источник