Матрица это что простыми словами
Значение слова «матрица»
1. Тех. Углубленная металлическая форма, применяемая при обработке металла давлением, при отливке типографских литер и пр. Линотипная матрица.
2. Типогр. Обратная (углубленная) копия, снимаемая с набора на картоне, свинце, пластмассе и т. п. для отливки стереотипов, с которых производится печатание.
3. Мат. Система каких-л. математических величин, расположенных в виде прямоугольной схемы.
[От лат. matrix, matricis — матка]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Матрица (искусство и техника) — образец, модель, штамп, шаблон, инструмент в серийном производстве объектов искусства и техники.
Матрица (диск) — название специального диска, служащий образцом для создания дисков (компакт-диск, DVD и др.) с записью (музыки, фильмов и т. д.) при их серийном или массовом производстве.
Матрица (издательское дело) — вогнутая часть формы, в которой пластическое тело формуется давлением, служащее типографским шрифтом.
Матрица в красильном деле — деревянная пластинка с вырезанным на ней рельефом какого-нибудь узора, служащая для отливки металлических набивных форм.
Матрица композита — связующее композиционного материала: распределяет нагрузку по армирующим элементам и защищает их.
Матрица как прямоугольная таблица:
Матрица (математика) — прямоугольная таблица элементов некоторого кольца или поля.
Матрица (программирование) — двумерный массив.
Матрица (электроника) — обобщенный термин для различных объектов в электронике, в которых элементы объекта упорядочены в виде двумерного массива, аналогично математической матрице.
Мáтричный индикáтор — разновидность знакосинтезирующего индикатора, в котором элементы индикации сгруппированы по строкам и столбцам.
Матрица (фото) — полупроводниковая СБИС с прямоугольной матрицей светочувствительных элементов (фотодиодов) для преобразования поступающего на неё света (отраженного от объекта) в электронный сигнал (изображение) или массив цифровых данных.
Матрица (экономика) — таблицы, предназначенные для диагностики состояния.
МА’ТРИЦА, ы, ж. [нем. Matrize] (тех.). 1. Пластинка с выдавленными, вырезанными обратными знаками или изображениями чего-н., служащая формой для отливки или штамповки. С матриц отливают типографские литеры. Матрицы употребляются при чеканке монеты. 2. Бумажная форма, являющаяся обратной копией набора и служащая для отливки стереотипа (тип.). Печатать что-н. с матриц.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
ма́трица
1. техн. форма с углубленным изображением рисунка, используемое во многих технологических процессах
2. техн. система каких-либо элементов, расположенных прямоугольником ◆ Матрица светочувствительных элементов.
3. матем. математический объект в виде таблицы чисел (или других сходных математических объектов) ◆ Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: агрегат — это что-то нейтральное, положительное или отрицательное?
Матрица
Ма́трица (нем. Matrize, от латинского matrix — матка, источник, начало)
1) сменный элемент литейной формы с углублённым (иногда фотографическим) изображением буквы или знака, используемый при отливке типографских литер или шрифтовых строк. М. — металлический брусок, на одной из граней которого выштамповано (путём вдавливания пуансона) или выгравировано очко буквы или знака. При заполнении жидким сплавом полости литейной формы и очка на М., прижатой к форме, образуются типографские литеры или шрифтовые строки с рельефной печатной поверхностью. В зависимости от типа машины, на которой производится отливка литер или строк, различают шрифтолитейные, строкоотливные и буквоотливные М.
Шрифтолитейная М. — стальной брусок прямоугольного сечения с углублённым изображением одной буквы или знака. Комплект шрифтолитейных М. позволяет отливать на шрифтолитейной машине все литеры одного шрифта, используемые для ручного набора.
В строкоотливной наборной машине (см. Линотип) из отдельных М., хранящихся в магазине, составляется матричная строка, устанавливаемая перед щелью литейной формы. После заполнения формы сплавом образуется цельнометаллическая шрифтовая строка.
В буквоотливной наборной машине (см. Монотип) комплект М. собран в матричной рамке. При отливке необходимая М. устанавливается над щелью отливной формы. В отличие от строкоотливной шрифтовая строка на буквоотливной наборной машине образуется из отдельных литер. Монотипная М. снабжена отверстием для нанизывания на стержень матричной рамки и коническим углублением для точной установки и прижима М. к литейной форме.
В фотонаборных машинах (См. Фотонаборная машина) используются М., в которых углублённые изображения знаков заменены фотографическими.
2) Углублённый оттиск с рельефной печатной формы на пластичном материале (картоне, пластмассе и т. д.), используемый для получения стереотипных копий печатной формы (см. Матрицирование, Стереотипия).
в математике, система элементов aij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m × n)-матрице. Обозначения:
или 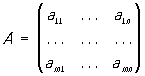
Короче: 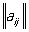
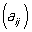
Действия над матрицами. Произведением прямоугольной (m × n)-матрицы А на число ее называют М., элементы которой получены из элементов aij умножением на число α:
Сумма определяется для прямоугольных М. одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, то есть
Умножение М. определяется только для прямоугольных М. таких, что число столбцов первого множителя равно числу строк второго. Произведением (m × р)-матрицы А на (р × n)-матрицу В будет (m × n)-матрица С с элементами
Введённые три действия над М. обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении М.: равенство AB = BA может не выполняться. Матрицы А и В называются перестановочными, если AB = BA. Кроме того, произведение двух М. может равняться нулевой М., хотя каждый сомножитель отличен от нулевой. Справедливы правила:
Определитель произведения двух квадратных М. равен произведению определителей перемножаемых М.
Часто удобно разбивать М. на клетки, являющиеся М. меньших размеров, проводя разделительные линии через всю М. слева направо или сверху вниз. При умножении такой так называемой клеточной М. на число, нужно умножить все её клетки на то же число. При надлежащем согласовании разбиений действия сложения и умножения клеточных М. осуществляются так, как будто вместо клеток стоят числа.
есть сходящийся на всей комплексной плоскости ряд (например, 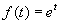
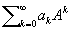
Аналитические функции от М. играют большую роль в теории дифференциальных уравнений. Так, система обыкновенных дифференциальных уравнений с постоянными коэффициентами, записанных в матричных обозначениях в виде
(здесь Х — столбец из неизвестных функций), имеет решение х = e At C, где С — столбец из произвольных постоянных.
Ненулевой столбец Х такой, что AX = λХ, называется собственным вектором М. А. В этом равенстве коэффициент λ может быть лишь одним из корней многочлена
Исчисление матриц. М. — полезный аппарат для исследования многих задач теоретической и прикладной математики. Одной из важнейших задач является задача нахождения решения систем линейных алгебраических уравнений. В матричных обозначениях такие системы записываются в виде
Не менее важной для многочисленных приложений (в теории дифференциальных уравнений, в теории малых колебаний, в квантовой механике и т. д.) является задача решения полной или частичной проблемы собственных значений. Здесь ищутся все или часть собственных значений М. и принадлежащие им собственные или корневые (некоторые обобщения собственных) векторы. К этой задаче близко примыкает и обобщённая проблема собственных значений, в которой ищутся числа и векторы такие, что AX = λBX (А и В — заданные М.), и многие родственные проблемы.
Ввиду большой практической важности поставленных задач для их численного решения имеется большое число различных методов. Наряду с нахождением численного решения важно оценивать качество найденного решения и исследовать устойчивость решаемой задачи.
Матрицы специального типа. Существует большое число различных типов М. в зависимости от выполнения различных соотношений между элементами.
| Название матрицы | Определяющее условие |
|---|---|
| Симметричная | 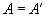 |
| Кососимметричная | 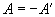 |
| Ортогональная | 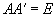 или или 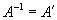 |
| Стохастическая | 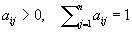 |
| Эрмитова | 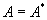 |
| Унитарная | 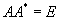 или или 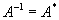 |
Некоторые типы естественно возникают в приложениях. Приведённая таблица даёт ряд важных типов квадратных М.
Следует отметить также ленточные М. — такие М., ненулевые элементы которых могут располагаться на главной диагонали и на диагоналях, соседних с главной, например, двухдиагональные и трёхдиагональные М. Не менее важны специальные типы М., употребляемых в качестве вспомогательных. Это элементарные М. — М., отличающиеся от единичной одним элементом; М. вращения и отражения.
Имеются унитарные аналоги М. вращения и отражения; правые (левые) треугольные М. — М., у которых равны нулю элементы под (над) главной диагональю; правые (левые) почти треугольные М. (М. типа Хессенберга) — М., у которых равны нулю элементы под (над) диагональю, соседней снизу (сверху) с главной.
Преобразование матриц. Численные методы решения систем линейных уравнений основываются обычно на преобразовании систем посредством цепочки левых умножений на подходящие вспомогательные М. с тем, чтобы перейти к легко решаемой системе. В качестве вспомогательных для вещественных М. употребляются элементарные М., М. вращения или М. отражения. Система с неособенной М. приводится либо к системе с треугольной М., либо с ортогональной. В теоретическом аспекте это равносильно представлению М. коэффициентов в виде произведения двух треугольных М. (при выполнении некоторых дополнительных условий) или в виде произведения треугольной на ортогональную (в том или другом порядке).
Для переопределённой системы умножением слева на цепочку М. вращения или отражения можно прийти к системе с треугольной М. порядка n, решение которой даёт обобщённое решение исходной системы.
Для решения проблемы собственных значений, раньше чем применять наиболее эффективные итерационные методы, целесообразно подобно преобразовать М. общего вида к М. типа Хессенберга или к трёх диагональной в случае симметрии. Этого можно добиться за счёт цепочки подобных преобразований элементарными М., М. вращения или М. отражения.
Историческая справка. Понятие М. было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И. А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и её приложениях. Исчисление М. развивается в направлении построения эффективных алгоритмов для численного решения основных задач.
Лит.: Смирнов В. И., Курс высшей математики, 9 изд., т. 3, ч. 1, М., 1967; Мальцев А. И., Основы линейной алгебры, 3 изд., М., 1970; Гантмахер Ф. Р., Теория матриц, 3 изд., М., 1967; Уилкинсон Дж. Х., Алгебраическая проблема собственных значений, перевод с английского, М., 1970; Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М. — Л., 1963; Воеводин В. В., Численные методы алгебры. Теория и алгорифмы, М., 1966; Лаппо-Данилевский И. А., Применение функций от матриц к теории линейных систем обыкновенных дифференциальных уравнений, М., 1957; Фрезер Р. А., Дункан В., Коллар А., Теория матриц и её приложения к дифференциальным уравнениям и динамике, перевод с английского, М., 1950; Вазов В., Форсайт Дж., Разностные методы решения дифференциальных уравнений в частных производных, перевод с английского, М., 1963.
Значение слова матрица
матрица в словаре кроссвордиста
матрица
Словарь медицинских терминов
пластинка для временного замещения отсутствующей стенки зуба при его пломбировании.
Имена, названия, словосочетания и фразы содержащие «матрица»:
Толковый словарь живого великорусского языка, Даль Владимир
ж. изложница, льяло, льяк, гнездо, форма для отливки печатальных букв. Матрицовый или матричный, относящийся к матрице.
Толковый словарь русского языка. Д.Н. Ушаков
матрицы, ж. (нем. Matrize) (тех.).
Пластинка с выдавленными, вырезанными обратными знаками или изображениями чего-н., служащая формой для отливки или штамповки. С матриц отливают типографские литеры. Матрицы употребляются при чеканке монеты.
Бумажная форма, являющаяся обратной копией набора и служащая для отливки стереотипа (тип.). Печатать что-н. с матриц.
Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
Зеркальная копия печатной формы, служащая для отливки стереотипов. Картонная, пластмассовая, свинцовая м.
Таблица каких-н. математических элементов, состоящая из строк и столбцов.
В нек-рых инструментах: деталь для обработки металла давлением.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
Углубленная металлическая форма, применяемая при штамповке металла, при отливке типографских литер и т.п.
Обратная углубленная копия, снимаемая с набора на картоне, свинце, пластмассе и т.п., для отливки стереотипов, с которых производится печатание.
Система каких-л. математических величин, расположенных в виде прямоугольной схемы.
Энциклопедический словарь, 1998 г.
металлическая пластинка с углубленным прямым изображением буквы или знака, изготовленная штамповкой пуансоном или гравированием. Служит формой для отливки литер в шрифтолитейном и наборном производствах.
Лист пластичного материала с углубленным изображением текста и рисунков, полученный прессованием с оригинальной формы высокой печати. Применяют при изготовлении стереотипов; хранится вместо набора (для целей переиздания, децентрализации печатания многотиражных изданий).
Рельефная копия штампа (контр-штамп), используемая при конгревном тиснении.
Имена, названия, словосочетания и фразы содержащие «матрица»:
Большая Советская Энциклопедия
Имена, названия, словосочетания и фразы содержащие «матрица»:
Википедия
Матрица :
Матрица как прямоугольная таблица:
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
Относительно сложения матрицы образуют абелеву группу ; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом ( векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.
Матрица среда, в которую помещаются изолированные активные частицы (атомы, молекулы, ионы, наночастицы и т. д.) с целью предотвращения взаимодействия между собой и с окружающей средой.
Шрифтолитейная матрица употреблялась в ручном наборе, а линотипная или монотипная — в механизированных наборных машинах.
Имена, названия, словосочетания и фразы содержащие «матрица»:
Примеры употребления слова матрица в литературе.
Уравнения Ногучи представляли собой комплекс вариабельных полевых матриц, позволявших бортовому ИИ более точно рассчитывать эффекты влияния кривых близкого пространства на особые Точки находившихся на орбите кораблей и устанавливать их с большей точностью.
Даже допечатка с готовых матриц по закону требует отдельного письменного соглашения.
Некоторые закупоривания могут происходить в фильтровальных матрицах, однако имеющиеся данные свидетельствуют, скорее, о широкомасштабном обледенении внутри труб.
Он с силой выбрасывает жидкую пластмассу из цилиндра в матрицу через инжекторный канал, проходя через который она разбрызгивается.
Это остаток пуповины из пластической массы, которая во время охлаждения соединяет матрицу с цилиндром через инжекторный канал.
На одной матрице были хорошо видны в лупу крошечные фигурки разных животных.
А с помощью одной бронзовой матрицы стало возможно начеканить из тонкого золотого листа уже целое стадо совершенно одинаковых оленей.
Тридцать сторон, изготовление матриц, гравировка через пантограф двадцати нумерованных экземпляров каждой стороны.
Кроме элементов, представляющих переигрывание действительной ситуации плода на каждом конкретном этапе родов, базовые перинатальные матрицы включают различные природные, исторические и мифологические сцены из трансперсональных сфер, обладающие похожими эмпирическими качествами.
Лилля, исстари обладавших прекрасным набором всех разновидностей готической печати, и старинной гарлемской типографии Эншеде, которая славилась своей культурой пуансона и матриц.
Источник: библиотека Максима Мошкова
Транслитерация: matritsa
Задом наперед читается как: ациртам
Матрица состоит из 7 букв
 lsvsx
lsvsx
Всё совершенно иначе!
Истина где-то посередине. Так давайте подгребать к ней не теряя достоинства.
Фильм «Матрица» вышел не так давно и уже снискал себе огромную славу. Он даже успел стать культовым фильмом нашего времени. Удивительно, но как точно авторы фильма увидели многие тонкие философские моменты, которые пытались передать людям и «просветленные” мира сего и многие великие философы.
Мы в ловушке. Этим миром правят жестокие и бездушные машины, а нас они используют просто в качестве «батареек».
Большинство зрителей, конечно, скоро оправятся от этого шока и снова «поверят” в реальность происходящего.
Они будут есть, пить, веселиться, уверенные в том, что это и есть настоящая жизнь.
В чем философия Вед и Матрицы?
Синяя таблетка Матрицы
Красная таблетка реальности
Может быть, этот путь также займет не одну жизнь… Но что с того? Никакая цена не будет слишком высокой, ибо ты возвращаешься в реальность, навсегда оставляя путы иллюзии.
Но те, кто выдержит, тем откроется Путь Домой, в намного более прекрасный мир, чем в фильме.
А пока мы еще здесь и витаем над этим миром Матрицы, не будучи уже его частью, нам остается только пытаться раскрыть глаза другим, таким же ищущим истину душам, которые тоже начали догадываться, что «в этом мире что-то не так».
И тогда мы сможем взять эту душу с собою и сказать ей те же слова, которые когда-то сказали нам:
Это верно: только совместные усилия учителя и ученика приводят к успеху.
Вот такой удивительный фильм гуляет сейчас по экранам. Только кто из зрителей действительно поймет глубинный смысл этого фильма? Может быть, ты?
Почему мы попали в Матрицу?
Почему мы находимся в Матрице? А если мы в неё попали, то откуда?
А если можно из неё освободится, то куда направиться? Что для этого нужно?
Мудрецы, духовные учителя прошлого, раскрывали и раскрывают знание, как преодолеть Матрицу. И авторитетом может быть только тот учитель, который получил это знание от своего учителя, полученной по цепи преемственности, начиная от источника всего мироздания – Господа.
Карма как космический закон
В послании Павла говорится: «Что человек посеет, то и пожнёт”.
Поэтому бесполезно и глупо искать ответственных за наше счастье или страдания. Индийская пословица гласит: «Когда я одним пальцем указываю на другого, то три указывают на меня”.
Но, если речь идёт обо всём мире, то необходимо принять существование космических норм добра и зла.
Эти нормы описаны в ведических произведениях и других явленных писаниях. Например, хорошими принимаются такие действия, как возлюбить ближнего своего, помогать тем, кто в беде, не прелюбодействовать и т.д.
Поняв космические нормы морали, человек способен в любой ситуации поступать правильно не на основе относительных правил, а на основе глобальной истины.
В своей жизни мы можем учиться на собственных примерах и ошибках и делать соответствующие выводы.
Каждое событие в нашей жизни должно стать для нас уроком космической морали. Тогда вся жизнь превратится в школу святости и восхождения к Свету, что приведёт нас к самосовершенствованию в течении одной жизни.
Как Матрица удерживает нас
С помощью чего Матрица удерживает нас здесь, в этом мире, который на самом деле является местом страданий?
Почему мы не видим этого? Как и с помощью чего она покрывает наше сознание так, что мы не видим этого? Почему, когда нам говорят об этом, мы не верим этому?
Матрица имеет всего несколько простых инструментов, с помощью которых она крепко удерживает нас в иллюзии.
Это наше желание быть независимым от изначального источника нашего появления – от Бога, и наше желание наслаждаться материальной природой – Матрицей. В конечном итоге эти желания означают только одно – желание самому стать таким своего рода богом, со своими владениями (домом, машиной, и др.), подданными (детьми, женой, подчиненными и т.д), богатствами (счетом в банке, золотом).
Но, ничего не подозревая, мы сами создаем себе прочнейшие цепи и кандалы, с помощью которых Матрица крепко удерживает нас в себе.
Это наши желания сексуальных наслаждений, все большего и большего количества денег и необходимой власти (даже над своей семьей), чтобы все это поддерживать. Как паук плетет себе паутину, так и мы создаем себе сети Матрицы, из которых потом не так-то просто выпутаться.
Эта низшая энергия майа со времен сотворения мира изумляет и завораживает души, равнодушные к Богу, и вводит их в заблуждение.
Ответ – да. Мы сами выбираем ту или иную ситуацию, тот или иной жизненный путь, и в дальнейшем соответственно получаем результаты того, что выбрали раньше. Никто, кроме нас самих, не создает страдания или счастье в нашей жизни. Мы ответственны за все, что происходит с нами, и когда мы начинаем понимать это, то мы становимся способны изменить свою жизнь к лучшему.
Тогда мы начинаем воспринимать все беды и препятствия в нашей жизни как своего рода испытание и жизненные уроки. А Матрица или майа – это энергия Господа, которая помогает нам проходить эти уроки, создавая для нас те или иные ситуации.
Это и есть так называемая школа жизни, через которую мы должны пройти с честью и достоинством и успешно сдать экзамены по ее окончанию.
Тогда мы сможем перейти на следующий уровень своего развития.
В ходе нашего обучения мы начинаем понимать, что все препятствия и помехи нужны для того, чтобы обучить нас и испытать наше усердие и постоянство.
А Матрица, или майа, как энергия Господа, может как стать нашим учителем, помогая нам, так и окончательно запутать нас в сетях наших же бесконечных желаний и их обескураживающих последствий.
В зависимости от нашего выбора мы воспринимаем реальность существования Матрицы, майи или даже Самого Господа. И соответственно формируется наше принятие или непринятие их как существующей реальности, и наше отношение к ним.
Так, например, когда врачи назначают горькие лекарства, диету или вскрывают скальпелем нарыв, то пациент может быть недоволен, полагая, что врач жесток, злонамерен и является его врагом. Но разумный человек понимает, что врач является его истинным благожелателем и только хочет помочь ему выздороветь.
Так и Божественная энергия, майа, погружая нас в различные ситуации и искушая, заставляет нас делать ежесекундный выбор между Добром и злом. Так, проходя эти жизненные уроки, ошибаясь и падая, перерождаясь жизнь за жизнью в различных телах, но, все же, опять поднимаясь и выбирая добро и свет, мы можем окончательно утвердиться в своем выбранном пути вперед, к Божественной Любви.
Матрица в древних источниках
Эта книга была открытием для нас. Мы были поражены, что тысячи лет назад информация о Матрице была известна. Более того, в ней сообщается, что Веды являются инструкцией к Матрице, материальной энергии. В Ведах содержится знание о том, как жить в Матрице так, чтобы жизнь стала освобождением из круговорота рождений и смертей.
Освобождение из Матрицы
Родившись в этом теле, я настолько себя с ним отождествил, что даже когда я говорю про себя, то думаю про это тело.
Что вкладывают Веды в понятие духа и материи?
Как научиться различать эти две энергии? Ответы на эти вопросы мы находим в «Бхагавад-гите»:
Иначе говоря, чтобы постичь разницу между материей и духом и научиться отличать их проявления, следует сначала постичь душу, т.е. себя самого.
Вот что говорит «Бхагавад-гита» по этому поводу: «Мудрецы, узревшие истину, пришли к заключению о бренности несуществующего (материального тела) и о неизменности вечного (души).
Они сделали этот вывод, тщательно изучив природу того и другого».
В своих комментариях на этот стих всемирно известный Духовный Учитель Шрила Прабхупада, пишет:
«Наше постоянно меняющееся тело не может существовать вечно. Современная медицина признает тот факт, что на клеточном уровне тело меняется каждое мгновение; это обусловливает процессы роста и старения. Но вечная душа, несмотря на все изменения, которые происходят с телом и умом, всегда остается неизменной. В этом разница между материей и духом. Понятие «существующий» относится исключительно к духу, а понятие «несуществующий» – к материи. Это утверждают все, кто видит истину».
Веды, как и другие священные писания мира, признают, что этот мир был сотворен в определенный момент времени. Подробности этого процесса, которыми пестрят целые тома ведической литературы, заставят призадуматься даже скептиков.
Действенной причиной творения является материальная природа, создающая все виды жизни и различные условия существования.
Также у сотворенного мира есть и смысловая причина.
Цель, или смысл мироздания состоит в том, чтобы дать живому существу (душе) возможность исполнить свои желания и, пресытившись материальными удовольствиями, постичь свое изначальное положение и вырваться из тьмы этого мира.
Иначе говоря, мы все также являемся причиной создания этого мира.
Изначальной и конструктивной причиной этого мира Веды провозглашают Кришну (по древнеславянски – Крышень), Верховную Личность Бога, Верховного повелителя и Творца всего сущего.
В древнейшей «Брахма-самхите» Кришну-Крышеня называют «причиной всех причин» и главной причиной творения. Это Тот, без кого творение невозможно. Однако способ, которым Он творит, в корне отличается от способов, известных нам.
Дело в том, что Бог не должен делать ничего Сам; для этого у Него существует масса слуг и помощников.
Иначе говоря, Бог действует посредством Своих энергий.
В разных частях ведических писаний мы находим подробные описание процесса творения.
Некоторые из них разнятся между собой, что говорит о том, что творение не происходит один раз в истории, но повторяется снова и снова, каждый раз с некоторыми вариациями.
Условия жизни на этих планетах также разнятся: шесть земных месяцев составляют день на высших планетах, а миллионы лет в аду равняются одной земной секунде.
На высших планетах живут полубоги, предки (человечества) и великие мудрецы, хранители вселенной.
На планетах земного типа живут существа, имеющие человеческий тип тела, а на адских планетах живут свирепые существа, которые пытают грешников.
Таково величие творения Бога, прославляемого в Ведах.

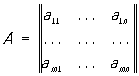
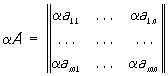
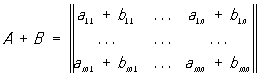
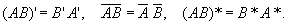
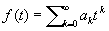
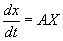
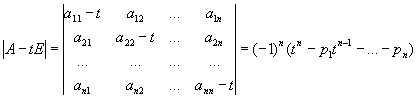
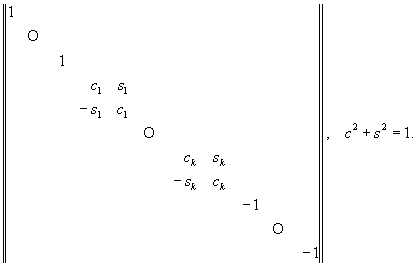
 lsvsx
lsvsx