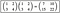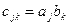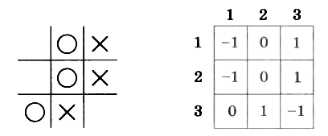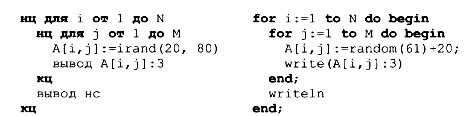Матрица и массив в чем разница

Математические операции над массивами и матрицами

May 31 · 4 min read

В процессе обработки и организации данных в определенные моменты возникает необходимость в выполнении математических операций над массивами и матрицами.

Заглянем в notebook

Чтобы ознакомиться с рассматриваемыми далее понятиями о математических операциях над массивами и матрицами в NumPy, загляните на страницу с Jupyter Notebook. Обратите внимание: для облегчения понимания важные функции, результаты выполнения и термины выделены жирным шрифтом.

Первым делом разберемся в различиях между массивами и матрицами в NumPy, где эти понятия рассматриваются немного по-разному.

Массив NumPy

Массивы NumPy — это многомерные объекты с размерностью N.

Матрицы NumPy

Матрицы NumPy — это д вумерные объекты. По сути, это те же массивы. Но есть массивы с размерностью 3, 4, 5 и т. д., а матрицы представляют собой массивы с размерностью 2.

Математически понятия остались неизменными — в практических и организационных целях разработчики NumPy лишь разделили методы и атрибуты, характерные для объектов- массивов, от тех, что характерны для объектов- матриц. Отметим также, что в операциях линейной алгебры над массивами и матрицами имеются некоторые различия, которые мы позже разберем.

Многие функции в NumPy в качестве получаемого в результате объекта возвращают массивы, а не матрицы. И не забывайте проверять тип объекта. Итак, начнем.

Загрузка пакетов

Создание матрицы 1

Проверка типа

Имеем объект-матрицу NumPy (матрицу NumPy), созданную с помощью функции matrix :

Создание матрицы 2

Другой метод создания матриц — список списков. Внутри этого списка еще два списка значений.

Создание матрицы 3

С помощью матричной функции создается также матрица со множеством строк и столбцов. При том, что NumPy выделяет создание такой матрицы в отдельную операцию, многомерный объект представляется все так же в виде массива:

Проверка типа

Получение среза матрицы

Кроме того, получают срез матрицы (не забывая, что индексация в Python начинается с 0):

Математические операции

Переходим к выполнению математических операций над массивами и матрицами.

Создание массива

Умножение массивов

Один массив умножается на другой:

Проверка типа

Преобразование массива в матрицу

Обратите внимание: объекты-массивы и объекты-матрицы практически одинаковы. Математически это одно и то же, но у нас для каждого из них есть методы и атрибуты.

Проверка типа

Умножение матриц

Матрицы тоже перемножаются друг с другом:

Почему результаты перемножения массивов и матриц отличаются?

При перемножении массивов происходит непосредственное умножение, т. е. элемент первого массива умножается на соответствующий элемент второго.

Скалярное произведение

При перемножении матриц происходит умножение каждого элемента строки первой матрицы на каждый элемент столбца второй матрицы с суммированием получаемого результата, затем следующий элемент строки первого массива умножается на следующий элемент столбца второго массива и т. д. То есть получаем операцию умножения строки * столбцы:

Этот метод, называющийся скалярным произведением, широко применяется в искусственных нейронных сетях, машинном обучении и искусственном интеллекте, причем практически везде это умножение матриц.

Тем не менее в NumPy выполняется и скалярное произведение массивов. Происходит оно так же, как обычное их умножение:

Скалярное произведение массивов

Мы получили тот же результат, что и при перемножении матриц:

Преобразование массива в матрицу

Массив в матрицу преобразовывается так:

Здесь мы воспользовались возможностью преобразования и перемножения матриц — скалярным произведением.

Преобразование матрицы в массив

Преобразуем матрицы в массивы и выполним операции над новым объектом.

Обратите внимание: результат операции приводит к умножению массивов на их соответствующие элементы.

Редко где в Интернете найдешь столь простое объяснение. Ведь для понимания этих различий требуются кое-какие математические знания.

Источник

r_d media

9 структур данных, которые вам понадобятся

Матрица, массив, стек и другие.

Еще в девяностые профессор Корейского университета передовых технологий Сонгчун Мун предложил Биллу Гейтсу назвать свой стартап Microdata, а не Microsoft. Мун указал на то, что данные и их структура — будущее программирования.

Структуры данных — способы хранения и извлечения информации. Правильный выбор структуры поможет эффективнее выполнить задачу. СД важны в разработке ПО, от них зависит, как будут работать алгоритмы.

Рассказываем о структурах данных, которые используются чаще всего.

#1. Массив (Array)

Массив — простая базовая структура. Стеки, очереди и списки — производные от массивов. Единице данных в массиве присваивается число или индекс, который указывает на ее расположение. Чтобы найти ячейку с информацией в массиве, нужно добавить к базовому элементу ее индекс. Базовый элемент, как правило, обозначается именем самого массива.

Представьте себе записную книжку со страницами, пронумерованными от 1 до 10. Каждая из них может содержать информацию или быть пустой. Блокнот — массив страниц, страницы — элементы массива «блокнот». Программно вы извлекаете информацию со страницы, обращаясь к ее индексу, то есть «блокнот+4» будет ссылаться на содержимое четвертой страницы.

Массив — это фиксированная структура, хранящая элементы одного типа в непрерывных ячейках памяти. Есть исключение — гетерогенные массивы, которые могут хранить данные разных типов. Массивы бывают одномерными и многомерными (массивы в массивах). Их размеры фиксированы, поэтому в уже созданный массив нельзя просто вставить новый элемент. Нужно скопировать старый массив и создать новый, увеличив размер.

#2. Матрица (Matrix)

Матрица — двумерный массив, выглядящий как список столбцов и строк, на пересечении которых находятся элементы данных. Это прямоугольный массив, в котором количество строк и столбцов задает его размер. В математике их используют для компактной записи линейных алгебраических или дифференциальных уравнений.

Матрицы используют для описания вероятностей. Например, для ранжирования страниц в поиске Google при помощи алгоритма PageRank. В компьютерной графике — для работы с 3D-моделями и проецирования их на двумерный экран.

#3. Связный список (Linked list)

Списки схожи с массивами, но отличаются более гибкой структурой. Они выглядят как цепочки нод или узлов, где каждая нода содержит ссылку на следующую. Доступ к элементам в связном списке осуществляется последовательно, в отличие от массивов с произвольным доступом. Списки бывают односвязными и двусвязными.

Начальный элемент этой структуры называется головой, а все последующие узлы цепочки — хвостом. Хвост состоит из элементов двух типов: с информацией (info) и с указанием на следующий узел (next). Конец цепочки обозначается как null.

#4. Стек (Stack)

Это вертикальный столбец с блоками, доступ к которым можно получить только с одного конца: сверху или снизу. Как в стопке книг — чтобы добраться до нижней, нужно сначала убрать все книги сверху.

Эта структура данных реализована в функции «отменить» (undo). Программа сохраняет статус работы так, что последнее действие становится первым в очереди на отмену. В стеке возможны всего три операции: добавление элемента (push), удаление (pop), чтение (peek).

Стек может быть реализован в виде связного списка или одномерного массива. В первом случае, каждый элемент содержит ссылку на следующий, во втором — упорядочен индексом.

Существует похожая СД — дек (deque — double ended queue, «двусторонняя очередь»). Это стек с двусторонним доступом.

#5. Очередь (Queue)

Этот тип СД напоминает стеки, но принцип работы реализован как FIFO (first in — first out, «первым пришел — первым ушел»). Как в супермаркете: первым покупки унесет домой тот, кто раньше всех займет очередь.

Очереди используются, когда ресурс нужно распределить между несколькими потребителями (работа ЦП, пропускная способность роутера). Или когда данные передаются асинхронно, то есть скорости приема и отдачи — разные.

В этой СД можно выполнить две операции: добавление элемента в конец очереди (enqueue) и удаление первого элемента (dequeue). Очереди бывают в виде связных списков или массивов, по аналогии со стеками.

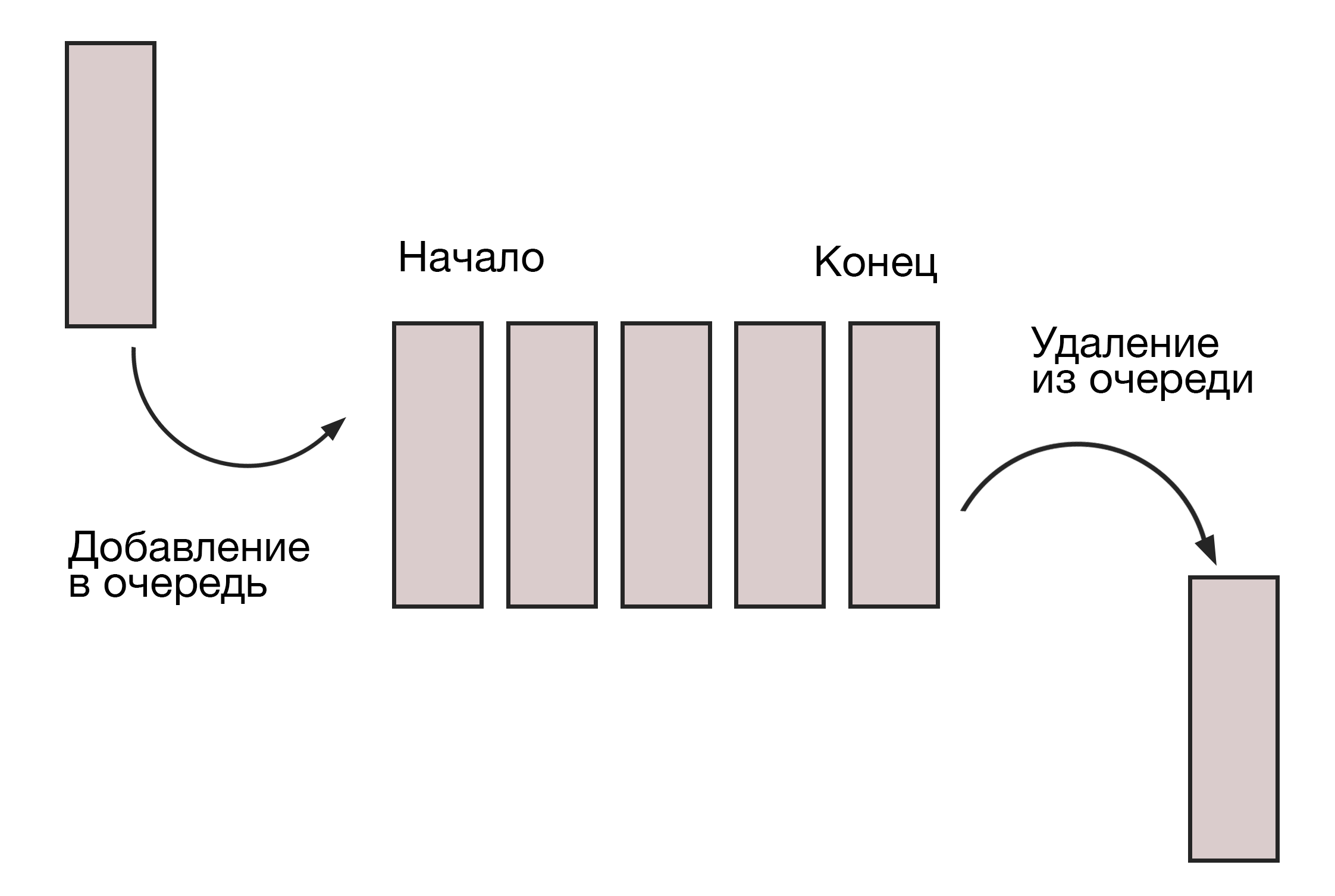
#6. Дерево (Tree)

Деревья — структура, в которой данные связаны между собой узлами, и при этом расположены иерархически. Различают двоичное дерево поиска, расширенное, черно-красное и еще десяток видов.

Как и у настоящего дерева, тут есть корни, ветви и листья. Самый верхний узел в этой СД, не имеющий предков, называется корневым. Остальные узлы — потомками или дочерними элементами. Дочерние узлы с одним и тем же родителем — это узлы-братья. А листья — это узлы, не имеющие потомков.

Деревья используют, например, в разработке видеоигр. Они позволяют разделить пространство и быстро находить объекты. Так, дерево с четырьмя дочерними узлами (quadtree) — квадрант — используется для создания карты и ориентации по четырем сторонам света в игре.

Но деревья сложно хранить и у них невысокая скорость работы.

#7. Куча (Heap)

Кучи — почти то же самое, что и деревья: у них также есть корневые и дочерние узлы. Отличается система иерархии: кучи бывают двух видов — те, где значения корневых узлов меньше и те, где значения больше, чем у дочерних. Эти СД можно хранить в простом или динамическом массиве, то есть они занимают гораздо меньше места, чем деревья.

Чтобы добавить новый элемент в кучу, нужно пересмотреть все остальные. Элементы расположены по убыванию — от больших к маленьким.

Кучи используют для сортировки объектов или реализации очередей с приоритетом.

#8. Префиксное дерево (Prefix tree)

Когда мы пользуемся автозаполнением, срабатывает структура данных, которая называется префиксным деревом. Это один из видов дерева поиска, который применяется, например, для хранения слов и быстрого поиска по ним. Узлы в этом дереве называются метками. Каждая метка содержит одну букву, поиск идет последовательно по меткам. Когда порядок букв начинает отличаться, дерево ветвится. Представьте, как смартфон предлагает целое слово, когда мы напечатали несколько букв.

Префиксное дерево используют в NLP и для синтаксического анализа естественных языков.

Обзор библиотеки Pillow.

Дата-сайентисты из Parimatch Tech — о рекомендательной системе, создании моделей и развитии data science.

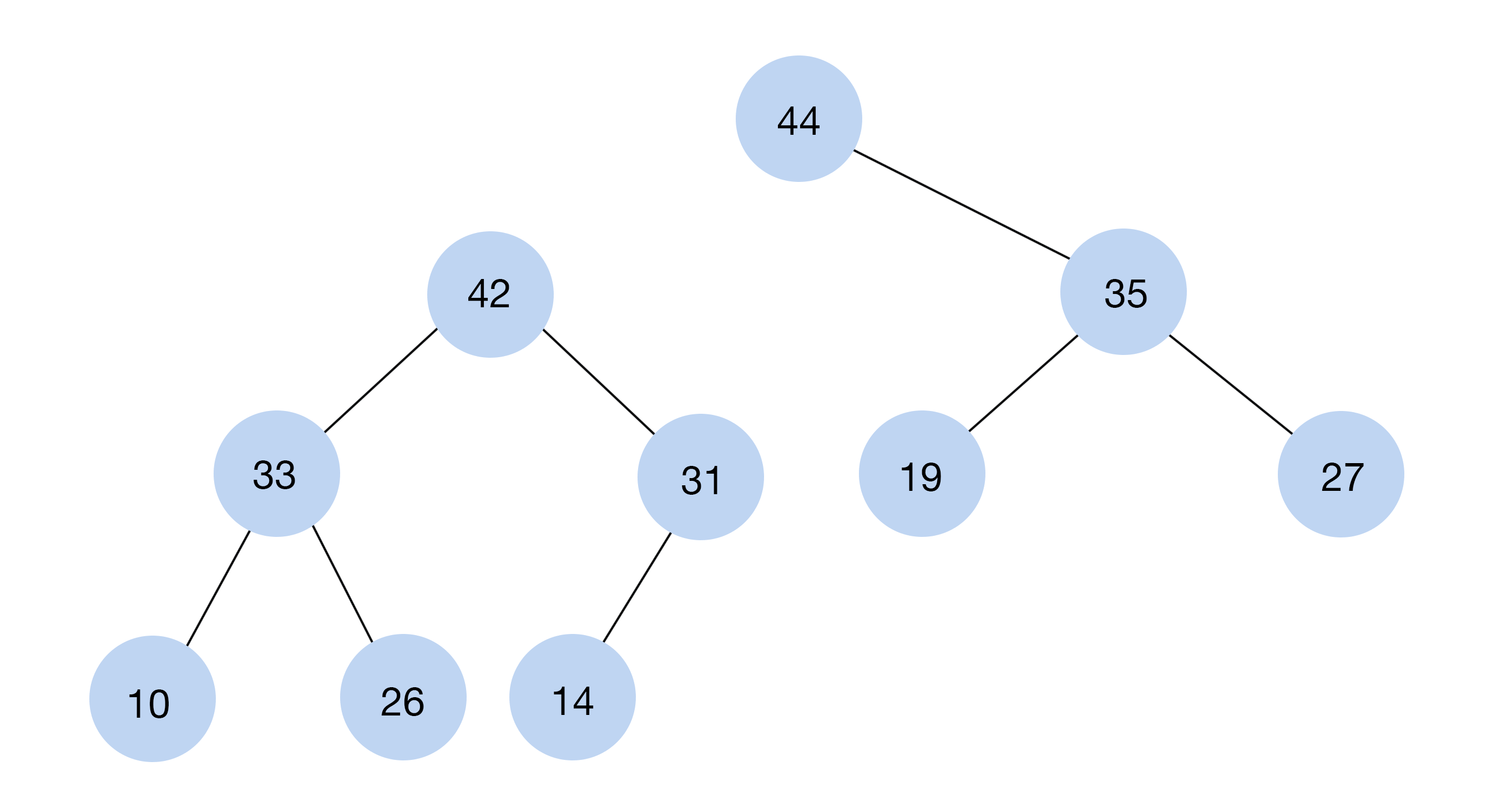
#9. Хеш-таблица (Hash table)

Хеш-таблица — это СД, в которой хранятся значения и связанные с ними ключи. Представьте большую библиотеку. Обычно для поиска книги там нужен справочник. Но можно использовать алгоритм хеширования, тогда функция сразу выдаст номер шкафа и расположение книги в нем. Это происходит благодаря ключам. Они содержат информацию для доступа к файлу и о его расположении. Хеширование используют в криптографии для шифрования информации.

Хеш-функция сокращает длинную строку символов до короткого значения. Это и будет ключом или индексом элемента данных в хеш-таблице. Набор данных в ней называется словарем.

Производительность хеш-таблицы зависит от функции хеширования, размера таблицы и метода обработки коллизий.

По материалам GeeksforGeeks, freeCodeCamp, Towards Data Science, а также исследованиям Альфреда Ахо, Джона Хопкрофта и Джеффри Ульмана.

Источник

Документация

MATLAB является сокращением от «матричной лаборатории». В то время как другие языки программирования в основном работают с числами по одному, MATLAB® спроектирован, чтобы работать, в основном, с целыми матрицами и массивами.

Создание массивов

Чтобы создать матрицу, которая имеет несколько строк, разделите строки точками с запятой.

Матричные операции и операции над массивами

MATLAB позволяет вам обрабатывать все значения в матрице с помощью одного арифметического оператора или функции.

Чтобы транспонировать матрицу, используйте одинарную кавычку ( ‘ ):

Можно выполнить стандартное умножение матриц, которое вычисляет скалярные произведения между строками и столбцами, с помощью * оператор. Например, подтвердите, что матрица, умноженная на её обратную матрицу, возвращает единичную матрицу:

Заметьте, что p не матрица целочисленных значений. MATLAB хранит числа как значения с плавающей точкой, и арифметические операции чувствительны к небольшим различиям между фактическим значением и его представлением с плавающей точкой. Можно отобразить больше десятичных цифр с помощью format команда:

Сбросьте отображение к более короткому формату используя

format влияет только на отображение чисел, а не то, как MATLAB вычисляет или сохраняет их.

Для каждого из матричных операторов умножения, деления и возведения в степень существует соответствующий оператор для поэлементных операций. Например, возведите каждый элемент a в третью степень:

Конкатенация

Конкатенация является процессом слияния массивов для создания бОльших массивов. На самом деле вы сделали свой первый массив путем конкатенации его отдельных элементов. Пара квадратных скобок [] оператор конкатенации.

Конкатенация массивов друг с другом, с использованием запятых, называется горизонтальной конкатенацией. Каждый массив должен иметь одинаковое число строк. Точно так же, когда массивы имеют одинаковое число столбцов, можно конкатенировать вертикально с использованием точки с запятой.

Комплексные числа

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация MATLAB

Поддержка

© 1994-2021 The MathWorks, Inc.

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник

Понятие массива. операции с матрицами и массивами

Все данные MATLAB представляет в виде массивов. Массив — упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя.

Массивы различаются по числу размерностей или измерений:

Размером массива называют число элементов вдоль каждого из измерений. Доступ к элементам осуществляется при помощи индекса. В MATLAB нумерация элементов массивов начинается с единицы. Это значит, что индексы должны быть больше или равны единице.

Вектор, вектор-строка, матрица или тензор являются математическими объектами, а одномерные, двумерные или многомерные массивы — способы хранения этих объектов в компьютере.

Вектор может быть записан в столбик (вектор-столбец) и в строку (вектор-строка).

Ввод, сложение и вычитание векторов

Простой пример работы с векторами – вычисление суммы векторов.

Пусть для хранения векторов используются массивы а и b.

Элементы массива вводятся в квадратных скобках с разделением точкой с запятой (вектор-столбец) или запятой (вектор-строка):

Для нахождения суммы векторов используется знак +.

Результат суммы векторов записывается в массив с:

Для нахождения разности векторов следует применять знак минус.

Если размеры векторов, к которым применяется сложение или вычитание, не совпадают, то выдается сообщение об ошибке.

Особенность MATLAB представлять все данные в виде массивов является очень удобной. Пусть, например, требуется вычислить значение функции sin сразу для всех элементов вектора с (который хранится в массиве с) и записать результат в вектор d. Можно использовать оператор присваивания:

Встроенные в MATLAB элементарные функции приспосабливаются к виду аргументов. Если аргумент является массивом, то результат функции будет массивом того же размера, но с элементами, равными значению функции от соответствующих элементов исходного массива.

Обращение к элементам вектора

Доступ к элементам вектора осуществляется при помощи индекса, заключаемого в круглые скобки после имени массива, в котором хранится вектор. Если среди переменных рабочей среды есть массив v, определенный вектором

то для обращения, например, к четвертому элементу используется индексация:

В результате переменной h присваивается значение 8.2.

Указание элемента массива в левой части оператора присваивания приводит к изменению в массиве. Например, выполнение выражения

приводит к тому, что второму элементу массива v присваивается значение 555.

Из элементов массива можно формировать новые массивы, например:

MATLAB предоставляет удобный способ обращения к блокам последовательно расположенных элементов вектора. Для этого служит индексация при помощи знака двоеточие. Пусть в заданном векторе w из семи элементов требуется заменить нулями элементы со второго по шестой. Индексация при помощи двоеточия позволяет просто и наглядно решить поставленную задачу:

Вектор можно умножить на другой вектор различными способами:

— скалярно (это произведение еще называют внутренним),

— образовать так называемое внешнее произведение.

Результатом скалярного произведения является число, векторного – вектор, внешнего – матрица, поэлементного – вектор.

Поэлементные операции с векторами

Показателем степени может быть вектор той же длины, что и возводимый в степень. При этом каждый элемент первого вектора возводится в степень, равную соответствующему элементу второго вектора.

К поэлементным относятся и операции с вектором и числом. Сложение вектора и числа не приводит к сообщению об ошибке. MATLAB прибавляет число к каждому элементу вектора. То же самое справедливо и для вычитания.

Скалярное произведение векторов а и b длины N, состоящих из действительных чисел, определяется формулой

.

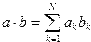
Следовательно, для вычисления скалярного произведения необходимо просуммировать компоненты вектора, полученного в результате поэлементного умножения а на b.

Векторное произведение a´b определено только для векторов из трехмерного пространства, т. е. состоящих из трех элементов. Результатом также является вектор из трехмерного пространства. Для вычисления векторного произведения в MATLAB служит функция cross.

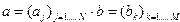
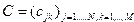
Внешним произведением векторов называется матрица размерностью N´M, элементы которой вычисляются по формуле

Вектор-столбец a в MATLAB представляется в виде двумерного массива размера N на один. Вектор-столбец b при транспонировании переходит в вектор-строку размера один на М. Вектор-столбец и вектор-строка есть матрицы, у которых один из размеров равен единице. Фактически 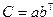, где умножение происходит по правилу матричного произведения. Для вычисления матричного произведения в MATLAB используется оператор умножения.

Статьи к прочтению:

Самоучитель C++ (21 серия) Visual Studio, Матрицы и многомерные массивы

Похожие статьи:

Для хранения матрицы используется двумерный массив. При вводе матрицы ее можно рассматривать как вектор-столбец из двух элементов, каждый из которых…

1. Дан двумерный массив размерностью 4 6, заполненный целыми числами с клавиатуры. Сформировать одномерный массив, каждый элемент которого равен…

Источник

Урок 37
§21. Матрицы (двумерные массивы)

Содержание урока

Что такое матрицы?

Что такое матрицы?

Ключевые слова:

Такие таблицы называются матрицами или двумерными массивами.

Матрица — это прямоугольная таблица, составленная из элементов одного типа (чисел, строк и т. д.).

Каждый элемент матрицы, в отличие от линейного массива, имеет два индекса — номер строки и номер столбца. На рисунке 4.3 серым фоном выделен элемент, находящийся на пересечении второй строки и третьего столбца — А[2, 3].

Определите значения элементов А[1,2], А[2,1] и А[3,3] на рис. 4.3.

Матрицу часто называют двумерным массивом, потому что каждый элемент матрицы имеет два индекса — номера строки и столбца.

При объявлении матриц указывают два диапазона индексов (для строк и столбцов):

цел N=3, М=4 const N=3; М=4;

целтаб А[1:N,1:М] var A: array[1..N,1..М] of integer;

Каждому элементу матрицы можно присвоить любое значение, допустимое для выбранного типа данных.

Поскольку индексов два, для заполнения матрицы нужно использовать вложенный цикл. Далее в примерах будем считать, что объявлена матрица из N строк и М столбцов, a i и j — целочисленные переменные, обозначающие индексы строки и столбца. В этом примере матрица заполняется случайными числами и выводится на экран:

Такой же двойной цикл нужно использовать для перебора всех элементов матрицы.

Запишите в тетради фрагмент программы, который вычисляет сумму всех элементов матрицы в переменной s.

Запишите в тетради фрагмент программы, который вычисляет количество ненулевых элементов матрицы в переменной к.

Следующая страница Обработка элементов матрицы

Cкачать материалы урока

Источник