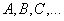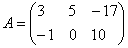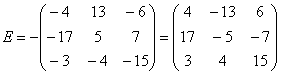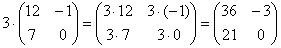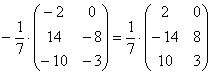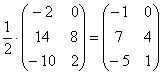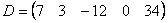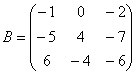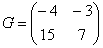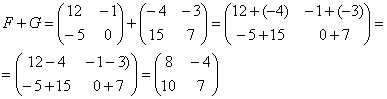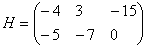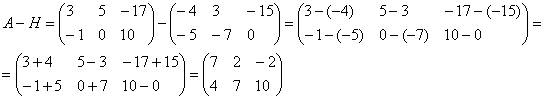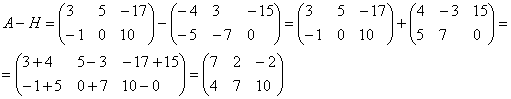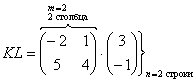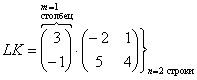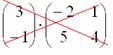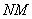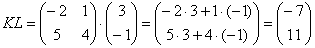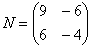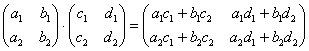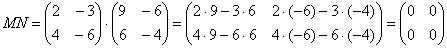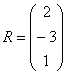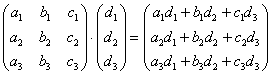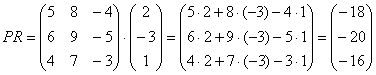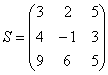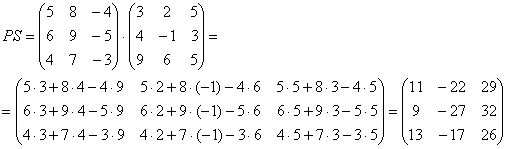Матрица в высшей математике для чего

Что такое матрицы, откуда они взялись, и чем они полезны?

Первые упоминания о матрицах или «волшебных квадратах», как их тогда называли, были найдены на территории еще Древнего Китая, однако бум случился намного позже, в середине XVIII века, когда знаменитый математик Габриэль Крамер опубликовал свой труд под названием «Введение в анализ алгебраических кривых», в котором описывался алгоритм решения систем линейных уравнений совершенно новым методом.

Как следствие, в дальнейшем появляются «классический» метод решения Карла Фридриха Гаусса, теорема Гамильтона-Кели, работы Карла Вейерштрасса, Георга Фробениуса и других выдающихся ученых.

Занимательно, что только после всех этих открытий, а именно в 1850 году был непосредственно введен термин матрица, автором которого стал Джеймс Джозеф Сильвестр.

Сегодня термин «матрица» применяется во множестве разных областей: от программирования до кинематографии (здесь должно быть название фильма, о котором вы все подумали).

Матрица в математике – это таблица чисел, состоящая из определенного количества строк (m) и столбцов (n).

Вы встречаетесь с ними каждый день, так как любая числовая информация, занесенная в таблицу, уже в какой-то степени считается матрицей.

Примером могут служить:
● список телефонных номеров;
● различные статистические данные;
● табель успеваемости ученика и многое другое.

Сами матрицы всегда обозначаются прописными латинскими буквами (A, B, C…), а элементы матрицы – строчными (a, b, c…). Индексы обозначают местоположение элемента матрицы в системе, причем первое число – это всегда номер строки, а второе – это всегда номер столбца. Например, а₂₃ находится во второй строке и в третьем столбце, а₃₁ в третьей строке и первом столбце и т.д.

Важно произносить элементы матриц правильно, так а₂₃ будет звучать как «а два три», а не «а двадцать три».

Примеры записи матриц

Для чего нужны матрицы

Теперь выясним, для чего нам так нужны матрицы конкретно в математике?

В качестве примера рассмотрим простейшую систему двух линейных уравнений и решим ее методом сложения, который изучают в школьном курсе.

Оказывается, можно решить эту систему уравнений альтернативным способом, используя матрицы, и называется он метод Крамера.

Вы можете подумать, зачем усложнять решение какими-то матрицами?

В данном случае да, при желании можно эту систему и в уме решить. Но представьте себе систему, состоящую хотя бы из 5 линейных уравнений с пятью неизвестными. А если система состоит из 6, 7 или ещё больше уравнений? Решать её школьным методом, мягко говоря, трудоёмко. Зато применяя тот же метод Крамера, решение будет выглядеть достаточно компактно.

Система с тремя уравнениями

В подтверждение вышесказанного рассмотрим систему уравнений с тремя неизвестными и решим её метод Крамера.

Из этого следует, что матрицы – еще один способ решения систем линейных алгебраических уравнений (СЛАУ).

На основе второго примера убеждаемся в том, что матрицы могут применяться в тех случаях, когда применение школьных методов решения СЛАУ не является рациональным.

На самом деле за прошедшие столетия алгебра матриц изучена более, чем достаточно, и тот факт, что матрицы используются повсеместно однозначно подтверждает необходимость их изучения.

Источник

Действия с матрицами

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.

Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!

Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов: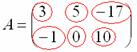

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: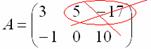

Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки: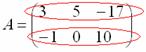

и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 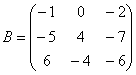– матрица «три на три».

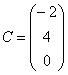
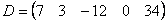
Если в матрице один столбец или одна строка , то такие матрицы также называют векторами.

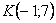
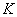
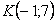
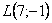
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

Вернемся к нашей матрице 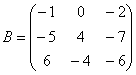. Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: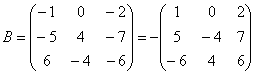

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: 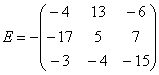. Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.

2) Действие второе. Умножение матрицы на число.

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

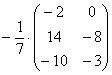
Сначала рассмотрим то, чего делать НЕ НАДО: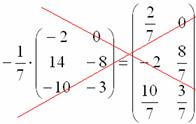

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если 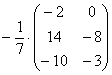– окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В этом случае можно и НУЖНО умножить все элементы матрицы на 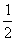, так как все числа матрицы делятся на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы.

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

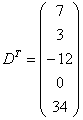
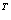
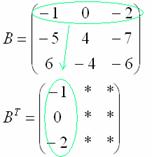
Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

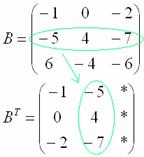
Потом переписываем вторую строку во второй столбец:

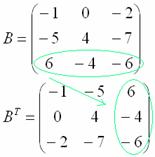
И, наконец, переписываем третью строку в третий столбец:

Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Сложить матрицы 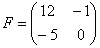и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Найти разность матриц ,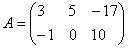

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :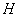

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

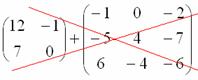
Какие матрицы можно умножать?

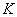
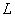
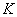
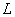
Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
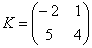
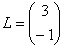
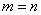
Можно ли умножить матрицу на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно:

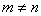
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
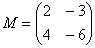
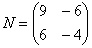
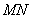
Например, для матриц, и возможно как умножение , так и умножение

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

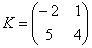
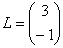
Умножить матрицу на матрицу
Я буду сразу приводить формулу для каждого случая:

– попытайтесь сразу уловить закономерность.

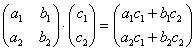
Умножить матрицу 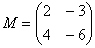на матрицу

Формула:

В результате получена так называемая нулевая матрица.

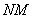
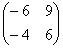
Попробуйте самостоятельно выполнить умножение (правильный ответ ).

Обратите внимание, что 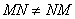! Это почти всегда так!

Таким образом, при умножении переставлять матрицы нельзя!

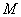
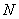
Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу 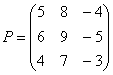на матрицу

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу 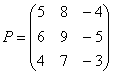на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.

А пока спектакль закончен.

После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

От действий над матрицами к пониманию их сути…

Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.

Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.

Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.

Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.

Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.

Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…

Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.

Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?

Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…

Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.

В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.

Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».

Источник