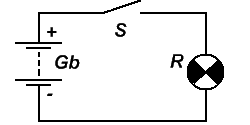Меандр что это в осциллографе
Чистый синус или модифицированный меандр
Чистый синус или модифицированный синус необходим для питания электрооборудования. ИБП с чистым синусом используются для электропитания оборудования с электродвигателями и компрессорами
Графики чистого синуса и меандра на экране осциллографа
Что такое «чистый синус» электропитания, и зачем он нужен? Давайте разбираться.
Качество электроэнергии, поставляемой в наши дома, отвечает определенным требованиям. Один из важных показателей качества — вид графика напряжения. График напряжения электрического сигнала в сети должен иметь правильную синусоидальную форму. Для такого графика часто используют определение «чистый синус».
В случае отключения сетевого электропитания используются источники бесперебойного питания. Однако далеко не все ИБП обеспечивают электропитание правильной синусоидальной формы.
Вид графика напряжения выходного сигнала источника бесперебойного питания зависит от типа и конструкции данного устройства.
Большинство обычных компьютерных ИБП генерируют на выход сигнал, называемый «модифицированный синус» или «меандр».
Различные типы графиков выходного сигнала, полученные с помощью осциллографа, представлены на следующем рисунке.
Методы аппроксимации графика чистого синуса
В этом разделе мы ознакомимся с различными методами аппроксимации графика чистого синуса, применяемыми на практике.
График напряжения в форме правильной синусоиды на следующих рисунках представлен красным цветом. Графики напряжения, имеющие приближенную к синусоиде форму, представлены другим цветом.
Самым простым приближением является график меандра. Меандр — простая ломаная линия, в данном случае имеющая форму прямоугольника в каждом полупериоде графика синуса. График простого меандра представлен на рисунке 1. На практике преобразователи такого типа не используются по причине резкого изменения значения напряжения в точках пересечения нулевого значения напряжения. Электрический сигнал такой формы создает большие электрические помехи и может вывести из строя подключенное оборудование.
Для снижения негативных эффектов применяется преобразование типа «меандр» с дополнительными «паузами» в точках смены полярности сигнала. График такого модифицированного меандра представлен на рисунке 2.
Более совершенные методы аппроксимации графика синусоиды напряжения позволяют получать график с большим количеством «ступенек». Такой подход позволяет снизить амплитуду перехода на следующую ступень и ближе подойти к графику «чистого синуса». Такой график носит название «модифицированный синус» и представлен на рисунке 3.
Когда нужен «чистый синус», а когда достаточно и «модифицированного»
Различные электроприборы и электрооборудование имеют разные требования к качеству электропитания. Ряд устройств корректно работает только с сигналом «чистый синус», другие приборы могут без проблем использовать электропитание в форме «модифицированного синуса». С другой стороны, источники бесперебойного питания с выходным сигналом в форме чистого синуса существенно дороже, чем ИБП с модифицированным синусом.
Не критичны к форме графика напряжения и могут использовать «модифицированный синус» следующие приборы:
Требуют использования питания форме чистого синуса следующие приборы:
Отклонения от правильной синусоидальной формы напряжения приводят к перегреву такого оборудования, повышенному трению и биению подвижных частей конструкции, к возможным авариям и поломкам. Использование источников питания с модифицированным синусом выходного сигнала приводит к существенному сокращению срока эксплуатации приборов, имеющих трансформаторные источники питания или электродвигатели.
ИБП с чистым синусом для питания котлов отопления
Для правильного и безопасного электропитания газовых котлов отопления необходимо использовать только ИБП с синусоидальной формой сигнала.
В конструкцию современного котла отопления входят: электронный блок управления, циркуляционные насосы, насосы или компрессоры для обогащения воздухом горючей смеси. Все эти устройства требуют правильного синусоидального электропитания.
Использование источников бесперебойного питания с формой сигнала в виде модифицированного синуса приведет к сбоям в работе электронного блока и повышенному износу и перегреву насосов котла отопления.
Надёжные российские источники бесперебойного питания компании БАСТИОН представлены в разделе Бесперебойное питание.
Гармонические колебания
На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

АЧХ шума.
Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).
Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.
Пару слов о матчасти
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания
Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:
где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:
ω=2 πf, где f — частота в Герцах.
Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.
Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал
Его сумма будет представлена следующей формулой:
Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.
Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.
Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)
Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.
Переходим к практическим упражнениям!
Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).
Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.
Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.
Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут
Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:
Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).
В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус
Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра
Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.
В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.
Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой с блекджеком и шлюхами, тем более, что это несложно.
Пишем свой анализатор спектра
Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.
Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.
Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.
Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек вектора исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.
Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.
Для начала алокируем массивы:
Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).
Массив для быстрого преобразования Фурье должен представлять собой последовательность
Виды электрических сигналов
Постоянный ток, является постоянно действующим электрическим сигналом.
Постоянный ток (напряжение), или постоянный сигнал – не изменяющийся по амплитуде и по знаку в течение продолжительного времени электрический сигнал. Источниками постоянного тока служат обычные гальванические элементы — батарейки, аккумуляторы, вторичные источники питания – адаптеры различных бытовых приборов, блоки питания, вмонтированные в различную аппаратуру. Привожу простейшую схему питания постоянным током и его временной (ударение ставить на «о») график (рис.1):
На схеме изображены: Gb – гальваническая батарея и R – сопротивление нагрузки (сигнальная лампа). Понятие постоянный сигнал используется, как правило, в элементах автоматики и цифровой логики и обозначает наличие, или отсутствие напряжения на входе, или выходе какого либо устройства. Состоянию «высокий уровень», или «логическая единица» (участок 3-4) соответствует наличие сигнала. Состоянию «низкий уровень», или «логический ноль» (участки 1-2 и 5-6) соответствует отсутствие сигнала.
К кратковременным сигналам относят: импульсы различной формы и пачки импульсов.
Импульс – это кратковременный сигнал. Импульс может иметь различную амплитуду I(U), длительность (τ) и форму, вплоть до хаотичной. Все эти параметры определяются источником этого импульса и элементами (электрической цепью) через которую он проходит, изменяясь при этом. На рисунке 2 изображена простейшая схема получения прямоугольного импульса и временной график одиночного прямоугольного импульса.
На схеме изображены: Gb – гальваническая батарея, S – выключатель, R – сопротивление нагрузки (сигнальная лампа). На временном графике показан действующий ток (напряжение) в различные временные отрезки:
— участок 1-2 когда S выключен – тока нет;
— участок 2-3 – в момент включения S – ток резко нарастает;
— участок 3-4 когда S включен – ток имеет постоянную величину, этот участок графика имеет свойство постоянного тока;
— участок 4-5 – в момент выключения S – ток резко уменьшается;
— участок 5-6 когда S выключен — тока нет.
Импульс, у которого длительность стремится к нулю, называется гамма-импульс. Объясню проще, гамма-импульс – это участок 2-3 – в момент включения выключателя S на рисунке 2. Выглядит гамма-импульс следующим образом:
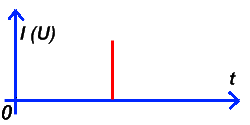
Источником гамма-импульса может быть любое замыкание электрической цепи, в результате которого происходит искровой разряд. Это может быть: природная молния, искра, возникающая при включении и выключении электроприборов, искра от коллектора работающего щёточного двигателя, или замыкающихся (размыкающихся) контактов реле.
Из всех видов электрических сигналов, гамма-импульс единственный, который присутствует во всех существующих в природе частотах.
В световом спектре: — в инфракрасном, в видимом, в ультрафиолетовом;
В радио спектре: — во всех диапазонах радиоволн;
В звуковом диапазоне: — на высоких и средних частотах, а с уменьшением частоты (где этим можно пренебречь), амплитуда гамма-импульса уменьшается до нуля.
Такое свойство гамма-импульса, назвали «белый шум». Другими словами говорят: Гамма-импульс имеет спектр частот «белого шума». Возьмите в руки радиоприёмник и встаньте недалеко от работающего сварщика. В моменты образования искры между электродом и свариваемым материалом, Вы увидите искру, кроме того, Вы услышите в приёмнике гул, забивающий сигнал от радиостанции, не зависимо от того, на какую частоту приёмник настроен, но ещё Вы едва услышите слабый звук шипения. Сварщик пользуется маской для того, чтобы не сжечь сетчатку глаз мощным ультрафиолетовым светом, исходящим от сварочной дуги.
Гамма-импульс так же является источником радиации. В зависимости от источника гамма-импульса, амплитуда его спектра в различных диапазонах частот так же различна, в том числе различно и воздействие на человека. Ведь человек не «облучается» радиацией от выключателя в комнате, или сварщик от своего сварочного аппарата.
Гамма-импульс тем больше выражен, чем больше его амплитуда и меньше сопротивление нагрузки. При этом его длительность максимально стремится к нулю, а частотный диапазон расширяется.

Известный всем Трансформатор Тесла работает благодаря гамма-импульсу. Если бы не было гамма-импульса в природе, то не было и самого Трансформатора Тесла. Моё личное мнение о возможности существования Водородного генератора Мэйера основывается так же на эффекте гамма-импульса, но это, я излагаю в другом разделе и статье.
Пачка импульсов – это серия импульсов, следующих друг за другом с установленными промежутками времени. В пачке, могут различаться как сами импульсы (по форме, амплитуде, длительности), так и промежутки времени их следования. Дистанционное управление различными радиоустройствами, как правило, производится сигналами, представляющими из себя пачки импульсов. Это пульты дистанционного управления телевизорами, другими бытовыми приборами, автомобильной сигнализацией, а так же более сложными устройствами.
Виды простых периодических сигналов
1. Переменный ток (напряжение) – изменяющийся по амплитуде и по знаку с определённым периодом T (частотой — ƒ). Обычно переменным током называют — синусоидальный ток. Все другие виды, которые мы рассмотрим ниже, это тоже переменный ток, но они имеют другие специфические названия. Источниками переменного синусоидального тока являются силовые генераторы различных типов и мощности на электростанциях, источники бесперебойного питания компьютеров, которые преобразуют постоянный ток аккумуляторных батарей в переменный ток. Переменный ток, а правильнее – переменное напряжение 220 вольт частотой ƒ = 50 Гц имеется в электрической розетке в каждом доме, если конечно дом не в пещере или глухом лесу. Привожу простейшую схему питания переменным током и его временной график:
На схеме: Е – генератор переменного тока. Как видно на графике, переменный ток можно охарактеризовать следующими параметрами: Амплитуда тока I – определяемого нагрузкой, амплитуда напряжения U и частота ƒ. Для всех видов переменного (периодически изменяющегося) тока имеется величина обратная частоте, её называют период T. Период связан с частотой простым выражением:
T = 1 / ƒ
К периодическим сигналам относят все ниже следующие виды сигналов и их разновидности. Источниками этих видов сигналов могут быть специальные генераторы или преобразователи.
2. Периодический прямоугольный сигнал – это сигнал, имеющий прямоугольную форму составляющих его импульсов, амплитуда которых постоянна (одинакова). Частота повторения импульсов ƒ периодического прямоугольного сигнала так же постоянна. Привожу временной график периодического прямоугольного сигнала:
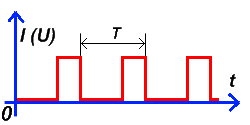
Кроме параметров характеризующих синусоидальный сигнал, прямоугольный сигнал характеризуется показателем – скважность импульсов (S) – это показатель, характеризующий отношение длительности импульсов к длительности их отсутствия.
3. Меандр – периодический сигнал прямоугольной формы, длительность импульса и длительность паузы которого в периоде равны. Другими словами, меандр — периодический прямоугольный сигнал со скважностью, равной 2. Все показатели, характеризующие прямоугольный сигнал, подходят и к Меандру. Привожу временной график меандра:
4. Пилообразный сигнал – это сигнал, имеющий пилообразную форму составляющих его импульсов, амплитуда и частота следования импульсов, которого постоянна. Привожу временной график пилообразного сигнала:
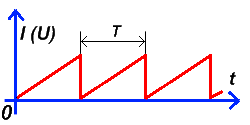
Рисунок 8: Пилообразный сигнал
Как и прямоугольный сигнал, пилообразный характеризуется показателями – амплитуда импульсов и частота следования (период следования) импульсов. Самое известное распространение пилообразного сигнала это – генераторы развёрток телевизоров и осциллографов с применением кинескопа (электровакуумной трубки).
5. Трапециевидный сигнал – это сигнал, импульсы которого имеют форму трапеции, амплитуда и частота следования импульсов, которого постоянна. Привожу временной график трапециевидного сигнала:
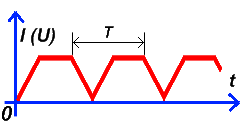
Рисунок 8: Трапециевидный сигнал
Трапециевидный сигнал характеризуется показателями – амплитуда импульсов, частота следования (период следования) импульсов. Это самый редкий из периодических сигналов. Были перечислены самые важные виды электрических сигналов, все остальные виды – это их модификации (комбинированные сигналы). Кроме того, все электрические сигналы, могут быть смещены, как в область более положительного напряжения, так и в область отрицательного напряжения, их название от этого не меняется. Со всеми вышеперечисленными сигналами Вы будете периодически сталкиваться в радиолюбительской практике.
Бывают более сложные виды сигналов, например модулированные сигналы:
— Амплитудно-модулированный сигнал;
— Частотно-модулированный сигнал;
— Фазо-модулированный сигнал;
— Фазо-частотно-модулированный сигнал;
— Фазо-кодо-манипулированный сигнал.
Меандр на осциллографе в чем причина и как убрать
Автор Гость Генадий,
5 ноября в Песочница (Q&A)
Рекомендуемые сообщения
Присоединяйтесь к обсуждению
Вы публикуете как гость. Если у вас есть аккаунт, авторизуйтесь, чтобы опубликовать от имени своего аккаунта.
Примечание: Ваш пост будет проверен модератором, прежде чем станет видимым.
Последние посетители 0 пользователей онлайн
Объявления
Сообщения
Похожий контент
Осёл с сенсорным экраном в формате планшета FNIRSI 1013D, б\у несколько раз, в комплекте 2 щупа, шнур тайп си, макулатура, в общем всё что и было кроме коробки. Обзоры и тесты смотрите в интернете
Ширина канала: 100 МГц * 2
Количество каналов: 2 канала + генератор 1кГц
Максимальная частота дискретизации в реальном времени: 1GSa/s
Вертикальная чувствительность: 50 мВ/див
500 В/Див
Горизонтальный диапазон времени: 50S/div
10 NS/div
Максимальное испытательное напряжение: 40 В (1X зонд), 400 В (10X зонд)
Глубина хранения: 240 кб
Входное сопротивление: 1 м
ADC точность: 8 бит
Режим напряжения: AC/DC
Режим запуска: одиночный, нормальный, автоматический
Тип триггера: Восходящий/нисходящий
Внешнее триггерное напряжение: 0 — 40В
Дисплей: 7 дюймов 800*480
Управление: емкостный сенсорный экран + жесты
Синхронизация: экспорт изображений USB
Источник питания: литиевая батарея 6000 мАч
Размер: 184 мм x 124 мм x 50 мм
Вес: 650 г
Ценник 8500 рублей
Мультиметр UNI-T UT50A, б\у, не ушатан, всё работает, какие то щупы в комплекте (не родные)
Не торгуюсь. Самовынос Речной\Трубная, отправка в регионы ТК Боксберри куда угодно за ваш счёт по предоплате на карту естественно ( имею профили с отзывами на авито, оверклокерc, vlab и т.д, также можно просто погуглить номер)
8-977-915-72-13 Дима