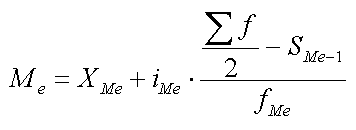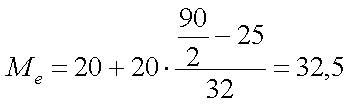Медиана балла что такое
Медиана
В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.
Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.
Понятие медианы
Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.
То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.
Формула для расчета медианы
Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.
Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.
Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:
Xme — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);
ime — величина медианного интервала;
f — частота (сколько раз в ряду встречается то или иное значение);
Sme-1 — сумма частот интервалов предшествующих медианному интервалу;
fme — число значений в медианном интервале (его частота).
Пример вычисления медианы
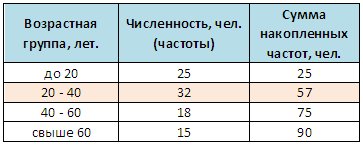
Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.
Область применения медианы
При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.
Особенности медианы
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Что вам говорит медиана?
Медиана обеспечивает полезная мера центра набора данных. Сравнивая медианное значение со средним значением, вы можете получить представление о распределении набора данных. Когда среднее и медиана совпадают, набор данных более или менее равномерно распределяется от наименьших до наибольших значений.
Тем не менее, для чего используется медиана?
затем: медиана обычно выше среднего?
Один из основных принципов статистики, который каждый студент усваивает примерно на второй неделе вводной статистики, заключается в том, что в асимметричном распределении среднее значение ближе к хвосту в искаженном распределении. Так что в правильное асимметричное распределение (хвост указывает прямо на числовую линию), среднее значение выше медианы.
тогда, о чем вам говорит разница между средним и медианным значением?
Когда использовать режим median vs mean VS?
В чем преимущества медианы?
Преимущества и недостатки средних
| Средняя | Advantage |
|---|---|
| медиана | На медиану не влияют очень большие или очень маленькие значения. |
| режим | Этот режим является единственным усреднением, которое можно использовать, если набор данных не числовой, например, цвета автомобилей на автостоянке. |
В чем разница между средним и медианным значением?
Что такое медиана и пример?
Медиана в статистике составляет среднее значение данного списка данных, при оформлении заказа. … Пример: медиана 2,3,4 равна 3. В математике медиана также является типом среднего, которое используется для нахождения центрального значения. Поэтому ее еще называют мерой центральной тенденции.
Всегда ли медиана ниже среднего?
Подводя итог, в целом если распределение данных смещено влево, среднее значение меньше медианы, которое часто меньше, чем у режима. Если распределение данных смещено вправо, мода часто меньше медианы, что меньше среднего.
Будет ли среднее или медианное значение выше?
Ответ: Среднее значение будет выше, чем медиана. Распределение набора данных, которое смещено вправо, является асимметричным и имеет большое количество значений на нижнем конце и несколько чисел на верхнем.
Может ли медиана быть ниже среднего?
Почему медиана используется для расчета дохода?
Средний семейный доход составляет более точный суммарный показатель дохода: Средний доход домохозяйства является более надежным и точным показателем для суммирования дохода на географическом уровне по сравнению со средним доходом домохозяйства, поскольку на него не влияет небольшое количество резко выделяющихся домохозяйств с чрезвычайно высоким или низким доходом.
В чем сходство и различие между средним значением медианы и модой?
Какая связь между средним значением и медианой?
Какая мера всегда является 50-м процентилем?
Какая мера центральной тенденции больше всего подвержена влиянию экстремальных ценностей?
Что является недостатком медианы?
Недостатки. Он не принимает во внимание точное значение каждого наблюдения. и, следовательно, не использует всю информацию, имеющуюся в данных. В отличие от среднего, медиана не поддается дальнейшим математическим расчетам и, следовательно, не используется во многих статистических тестах.
Каковы преимущества и недостатки использования медианы?
Преимущества и недостатки медианы
Каковы плюсы и минусы использования медианы в качестве меры центральной тенденции?
За: Обычно это лучший показатель центральной тенденции, потому что он использует все оценки.
В чем сходство между средним и медианным значением?
Ответ: среднее и медиана будут довольно близко друг к другу. Когда набор данных имеет симметричное распределение, среднее значение и медиана близки друг к другу, потому что среднее значение в наборе данных, когда оно упорядочено от наименьшего к наибольшему, напоминает точку уравновешивания данных, которая встречается в среднем.
Как рассчитывается медиана?
Расположите свои числа в числовом порядке. Посчитайте, сколько у вас чисел. Если у вас есть нечетное число, разделить на 2 и округлить чтобы получить позицию среднего числа. … Перейдите к числу в этой позиции и усредните его с числом в следующей более высокой позиции, чтобы получить медианное значение.
Объяснение: Для набора только двух значений медиана будет такой же, как среднее или среднее арифметическое. Для наборов данных это не так. Например, числа 2, 10 имеют среднее и медианное значение 6.
Как найти среднее значение?
Чтобы найти медиану, расположите все числа в порядке возрастания и продвигайтесь к середине, вычеркивая числа на каждом конце. Если данных много, прибавьте 1 к количеству элементов данных, а затем разделите на 2 чтобы найти, какой элемент данных будет медианным.
Как вы находите срединный пример?
Чтобы найти медиану,
сначала отсортируйте числа от наименьшего к наибольшему.
Затем найдите среднее число
. Например, средний для этого набора чисел 5, потому что 5 находится прямо посередине: 1, 2, 3, 5, 6, 7, 9.
Медиана (статистика)
Также медиану можно определить для случайных величин: в этом случае она делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2); более точное определение см. ниже.
Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
Связанные понятия
Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.
Упоминания в литературе
Связанные понятия (продолжение)
Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых.
Исследование моды и медианы результатов ЕГЭ по математике
Рубрика: Математика: алгебра и начала анализа, геометрия
Дата публикации: 04.06.2017 2017-06-04
Статья просмотрена: 719 раз
Библиографическое описание:
Демченко, В. В. Исследование моды и медианы результатов ЕГЭ по математике / В. В. Демченко, Н. А. Кораблев. — Текст : непосредственный // Юный ученый. — 2017. — № 3 (12). — С. 2-4. — URL: https://moluch.ru/young/archive/12/985/ (дата обращения: 11.12.2021).
Для получения более полной характеристики случайных величин кроме средней величины рассчитываются так называемые структурные средние. К ним относят моду и медиану. Данная статья представляет собой результаты исследовательского проекта.
Мода — это наиболее встречающееся значение признака, или, иначе говоря, значение признака, имеющее наибольшую повторяемость (частоту). Моду рассчитывают по-разному, в зависимости от того, как изменяется случайная величина — дискретно или непрерывно.
На практике чаще всего анализируемые данные оформлены в форме таблицы. В случае непрерывно изменяющейся случайной величины все ее значения разбиваются на интервалы по принципу «от и до». Для определения моды в случае непрерывно изменяющейся случайной величины сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем внутри интервала ведут расчет по формуле:
где 




Определить модальное значение признака можно и по графику. Для этого в случае дискретно изменяющихся случайных величин строится полигон распределения. На оси абсцисс откладываются значения признака, а на оси ординат — соответствующие им частоты. Значение абсциссы, соответствующие наибольшей вершине полигона, будет значением моды.
Для определения моды в случае непрерывно изменяющейся случайной величины строится гистограмма. В этом случае на оси абсцисс находятся значения границ интервалов значений случайной величины, а на оси ординат — соответствующие этим интервалам частоты. На гистограмме модальному интервалу будет соответствовать столбец, имеющий наибольшую высоту. Затем необходимо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускают перпендикуляр. Абсцисса этой точки и будет модой.
Ряд распределения случайной величины может содержать несколько модальных значений: имеющий одну моду, называется унимодальным, две — бимодальным, три и более — мультимодальным.
Медиана — это значение признака, которое делит все данные на две равные части: половина единиц совокупности имеет значения признака не меньше медианы, другая половина — значения признака не больше медианы.
В случае непрерывно изменяющихся случайных величин сначала определяют медианный интервал. Для этого рассчитывают порядковый номер медианы 


где 



Медиана может быть определена графически по кумуляте. Для этих целей на оси ординат, где отмечаются накопленные частоты, находится точка, соответствующая полусумме всех частот, т. е. порядковому номеру медианы. Из нее проводится прямая параллельно оси абсцисс до пересечения с графиком. Абсцисса точки пересечения и соответствует медиане.
Для определения медианы в случае дискретно изменяющихся случайных величин значения изучаемого признака ранжируют, т. е. располагают в порядке возрастания (или убывания). Если число единиц совокупности нечетное, то значение признака, находящееся в середине ранжированного ряда, будет являться медианой. Если число единиц будет четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.
В качестве практического примера рассмотрим результаты сдачи ЕГЭ по математике некоторой совокупностью учащихся в количестве 170 человек. При этом с некоторым допущением будем считать результат сдачи ЕГЭ непрерывно изменяющейся величиной, т. е. применим соответствующую формулу расчета. Данные представлены в таблице 1.
Данные о результатах сдачи ЕГЭ по математике по 100-бальной шкале
Величина балла по 100-бальной шкале (xi)
Количество учащихся (fi)
Медиана в статистике: понятие, свойства и расчет
Среднее значение
Часто так называют среднеарифметическое значение выборки (или множества чисел). Это, пожалуй, самый распространенный термин, из вышеперечисленных трех. Хотя бы потому, что почти каждый день мы слышим это слово в СМИ. Значение его тоже объясняет само название. Тем не менее, для тех, кому непонятен смысл этого слова, объясним “на пальцах”.
Это сумма данных чисел, деленное на количество. Если написать в виде формулы, это выглядит так.
Пример из практики
Медиана
Медиана – число, характеризующее выборку, т.е. если взять все элементы множества, то это число ровно делит множество пополам. Одна половина множества равна или больше этого число, а другая меньше или равна этому числу.
Пример из практики
Значит, среднее значение в год составляет
$(1,000,000 + 200,000 + 8,900) : 100 = 1,208,900 : 100 = 12,089$ у.е.
Зная соотношение неработающих людей, на каждого работающего, и поделив полученное на это число, получим доход на душу населения (с учетом детей, стариков и больных без пенсии).
Итак, такая статистика показывает, что народ живет припеваючи, зарабатывая примерно 1,000 у.е. в месяц, а действительность другая. Как раз, так и вычисляется доход на душу населения. Берется национальный доход и делится на численность населения. Теперь вы понимаете, почему в сводках всегда называют эту цифру, потому что она никоим образом не отображает благосостояние большинства, а только является показателем экономического благосостояния страны.
Пример из практики
Если постоять на проспекте и в течение 10 минут и посчитать все проезжающие автомобили и классифицировать их по цветам, то можно определить моду для цвета автомобилей этого города. Допустим, насчитали 95 белых, 45 черных, 12 красных, 38 серых и 70 других цветов. Значит, модой в этом городе являются автомобили белого цвета. Это хорошая информация для дистрибьюторов автомобилей.
Подробнее о среднем значении
Иногда вычисляют среднее значение для группы данных. Тогда значения разбивают на группы и вычисляют серединную точку каждой группы. Затем эти значения умножают на количество членов каждой группы (на частотность) и складывают. А результат делят на общее количество. Такое значение называют средним значением группы. Посмотрите на этот пример:
| Группа | Частота | Середина |
|---|---|---|
| 1-20 | 5 | 10.5 |
| 21-40 | 25 | 30.5 |
| 41-60 | 37 | 50.5 |
| 61-80 | 23 | 70.5 |
Умножаем эти значения на частоты и складываем, затем делим на общее количество:
Как уже показали на примере с доходом населения, экстремумы сильно влияют на среднеарифметическое значение, поэтому иногда полезно их отбрасывать. Тогда среднее значение называется урезанным средним.
В симметричном распределении (типа нормального распределения ) среднее значение, медиана и мода равны или близки друг другу. В асимметричном же, они отличаются, и число, на которое отличаются эти показатели, дают информацию о “скошенности” распределения относительно нормального.
Надеемся, что нам удалось “на пальцах” объяснить значение терминов среднеарифметическое значение, медиана и мода.
Связанные понятия
Упоминания в литературе
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
Для примера рассчитаем медиану по следующим данным.
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Определение моды и медианы по несгруппированным данным
| N п/п | 1 | 2 | 3 | 4 | … | 50 | 51 | … | 99 | 100 |
| Доход, долл. | 100 | 104 | 104 | 107 | … | 162 | 164 | … | 100 | 50 000 |
Если воспользоваться средней арифметической, то получим средний доход, равный примерно 600 – 700 долларов, который имеет мало общего с доходами основной части группы. Медиана же, равная в данном случае Me = 163 доллара, позволит дать объективную характеристику уровня доходов 99 % данной группы людей.
Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).
Предположим, распределение рабочих всего предприятия в целом по тарифному разряду имеет следующий вид (табл. 2).
Таблица 2 – Распределение рабочих предприятия по тарифному разряду
| Тарифный разряд | Численность рабочих, человек |
| 2 | 12 |
| 3 | 48 |
| 4 | 56 |
| 5 | 60 |
| 6 | 14 |
| ВСЕГО | 190 |
Определение моды по дискретному вариационному ряду
Определение моды и медианы графическим методом
Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Из точки их пересечения опускаем перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 3).
Рис. 3. Графическое определение моды по гистограмме.
Рис. 3. Графическое определение моды по гистограмме.
Рис. 4. Графическое определение медианы по кумуляте
Для определения медианы из точки на шкале накопленных частот (частостей), соответствующей 50 %, проводится прямая, параллельная оси абсцисс до пересечения с кумулятой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.
Неуникальность значения
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке <1, 2, 3, 4>медианой, по определению, может служить любое число из интервала (2,3)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений.
Как найти медиану чисел
Лучше рассмотреть процесс вычисления медианы на примере. Пусть у нас есть ряд чисел: 13 19 24 17 15 11. Для удобства числа будет записывать через пробел. Найдем его медиану. Для начала необходимо расположить числа в порядке возрастания. Эта процедура называется сортировкой. Получим новый ряд: 11 13 15 17 19 24. Так как количество чисел в ряду равно 6, а число 6 четное, то середина ряда будет между числами 15 и 17. Найдем среднее этих двух чисел: (15 + 17) / 2 = 16. Это и будет медианой ряда. Не стоит путать медиану, среднее гармоническое и среднее арифметическое — это принципиально разные понятия.
Рассмотрим другой пример, когда количество чисел в ряду нечетное. Есть такой ряд: 18 46 10 5 38. Найдем медиану набора этих чисел. Отсортируем ряд по возрастанию и получим ряд: 5 10 18 38 48. Так как количество чисел в этом ряду 5, то у него есть середина — это элемент с номером 2. Значит медиана этого ряда равна элементу с номером 2. Получаем ответ 18.
И еще пример — найдем медиану чисел 158 166 134 130 132. Отсортируем и получим ряд 130 132 134 158 166. Количество чисел нечетное и равно 5, значит средний элемент имеет номер 3. Третий элемент нашего отсортированного ряда — число 134. Это и есть медиана.
Область применения медианы
При вычислении типичного признака неоднородных рядов, имеющих «выбросы» – значения во много раз отличающиеся от других значений ряда.
Пример использования
Предположим, что в одной комнате оказалось 19 бедняков и один миллионер. У каждого бедняка есть 5 ₽, а у миллионера — 1 млн ₽ (10 6 ). В сумме получается 1 000 095 ₽. Если мы разделим деньги равными долями на 20 человек, то получим 50 004,75 ₽. Это будет среднее арифметическое значение суммы денег, которая была у всех 20 человек в этой комнате.
Медиана в этом случае будет равна 5 ₽ (полусумма десятого и одиннадцатого, срединных значений ранжированного ряда). Можно интерпретировать это следующим образом. Разделив всю компанию на две равные группы по 10 человек, мы можем утверждать, что в первой группе у каждого не больше 5 ₽, во второй же — не меньше 5 ₽. В общем случае можно сказать, что медиана — это то, сколько принёс с собой «средний» человек. Наоборот, среднее арифметическое — неподходящая характеристика, так как оно значительно превышает сумму наличных, имеющуюся у среднего человека.
Неуникальность значения
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке <1, 3, 5, 7>медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из элементов; в примере выше это число 3) и «верхней медианы» (элемент с номером (n+2)/2; в примере выше это число 5). Эти понятия определены не только для числовых данных, но и для любой порядковой шкалы.
Советы
Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.