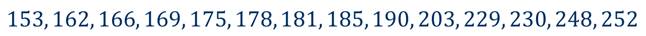Медиана это что в алгебре
Что такое медиана в алгебре
Здравствуйте!
Объясните, пожалуйста, что такое медиана в алгебре? В геометрии – это понятно, а про медиану в алгебре интересно узнать.
Спасибо!
Что такое медиана в алгебре.
Многочисленные количественные данные анализируют с помощью статистических исследований. При каждом исследовании происходит сбор и обработка информации.
Рассмотрим пример:
Ученик 9 класса получил следующие оценки:
9 4 7 4 8 9 10 5 12.
Ряд данных, которые были получены при статистическом исследовании, называют выборкой.
Каждое число ряда данных называют вариантой.
Объём выборки – это количество чисел ряда.
Чтобы найти среднее арифметическое ряда нужно сумму вариант разделить на объём выборки.
Если записать выборку в порядке, при котором каждая следующая варианта будет не превышать предыдущую, то такой ряд данных будет называться упорядоченным (вариационным).
Сколько раз варианта появится в выборке, такое число и называют частотой варианты.
Размахом выборки называют разница между наибольшей и наименьшей вариантами.
Варианта с наибольшей частотой называется модой выборки.
Если в ряду есть 2 или более вариант с одинаковой частотой (выбирается наибольшая частота), то все такие варианты являются модами.
Если все варианты имеют одинаковую частоту, то моды нет.
Медианой является варианта, которая стоит посередине ряда чисел, который упорядочен по возрастанию. В случае четного количества чисел ряда медианой является среднее арифметическое двух средних вариант.
Вернемся к примеру.
Запишем вариационный (или упорядоченный) ряд:
4 5 4 7 8 9 9 10 12.
Ее объем 9.
Среднее арифметическое:
(4 + 4 + 5 + 7 + 8 + 9 + 9 + 10 + 12) : 9 ≈ 7,56.
Размах: 12 – 4 = 8.
Моды: 4 и 9.
Медиана: 8.
Медиана как статистическая характеристика
Урок 11. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Медиана как статистическая характеристика»
· ввести понятие «медиана числового ряда».
На предыдущем уроке мы с вами познакомились с тремя статистическими характеристиками.
На этом уроке мы познакомимся с ещё одной статистической характеристикой.
Давайте рассмотрим таблицу, в которой показано число посетителей музея в разные дни недели.
Составим из данных, приведённых в таблице, упорядоченный ряд.
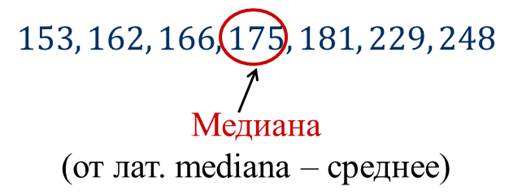
В этом ряду семь чисел. Посмотрите, что в середине ряда расположено число 175: слева от него расположены 3 числа и справа тоже 3 числа. Число 175 называют срединным числом, или медианой упорядоченного ряда.
Слово «медиана» произошло от латинского слова «медиана», которое означает «среднее».
Число 175 считают и медианой исходного (неупорядоченного) ряда.
Теперь рассмотрим таблицу, в которой показано число посетителей музея в разные дни в течение двух недель.
Снова составим из приведённых данных упорядоченный ряд.
Обратите внимание, что в этом ряду чётное количество чисел, и поэтому мы не можем выбрать одно число, расположенное в середине и выберем два – 181 и 185.
Найдём среднее арифметическое этих чисел, то есть их сумму разделим на 2, и получим 183. Число 183 разбивает наш ряд на две равные по численности группы (слева от него находятся 7 чисел ряда и справа – 7 чисел ряда) и является медианой упорядоченного ряда и исходного. При этом обратим внимание, что само число 183 не является членом ряда.
В каждом из рассмотренных примеров, найдя медиану ряда, мы можем указать дни, когда количество посетителей музея превосходит срединное значение, то есть медиану, или, наоборот, меньше этого значения.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине.
А медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, расположенных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана это что в алгебре
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Для ряда a1,a1. an среднее арифметическое вычисляется по формуле:
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.
Медиана — это золотое сечение треугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.
У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.
И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.
Медиана — это.
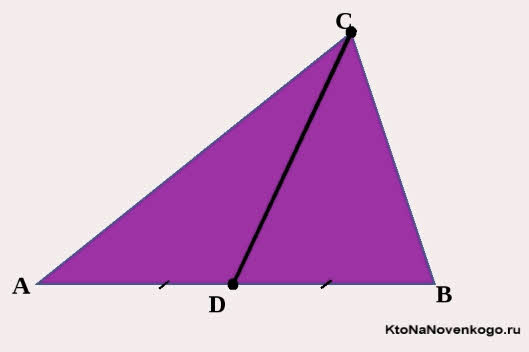
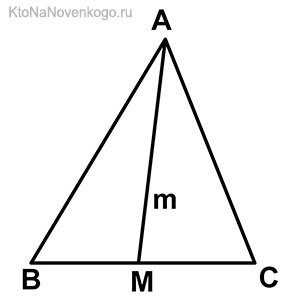
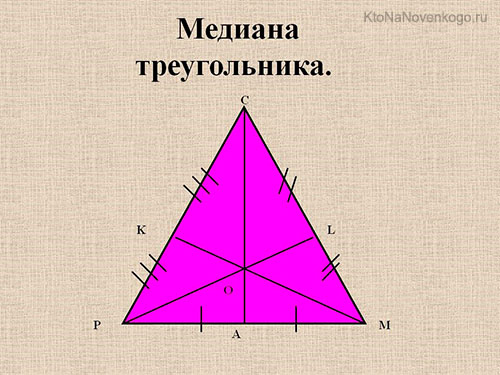
Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.
Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.
Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.
Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:
Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.
Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.
И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!
И выглядят они вот так.
На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.
Пересечение медиан треугольника
Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.
Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.
Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.
Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:
Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.
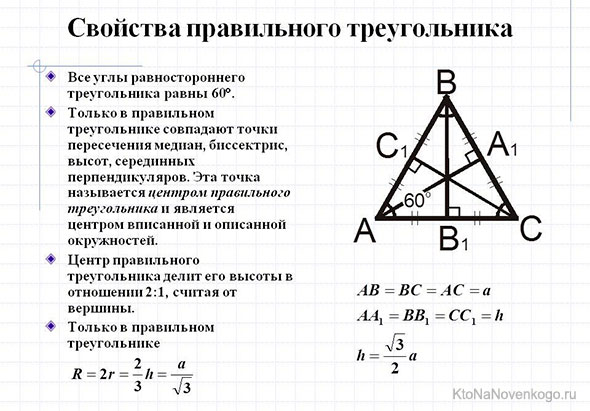
Медиана равностороннего треугольника
Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.
Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.
Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.
И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.
Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.
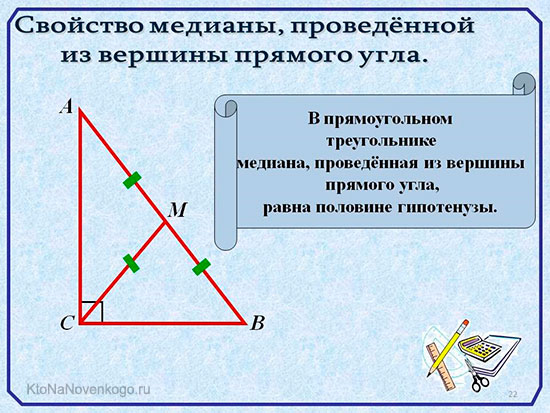
Медиана прямоугольного треугольника
Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.
Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.
Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.
Вместо заключения
А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.
Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.
Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».
И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.
Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Теперь остаётся подумать над тем, как применить это знание о медиане на практике. Если придумаю, вдруг Нобелевскую премию дадут?
Медиана (статистика)
Также медиану можно определить для случайных величин: в этом случае она делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2); более точное определение см. ниже.
Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
Связанные понятия
Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.
Упоминания в литературе
Связанные понятия (продолжение)
Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых.