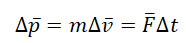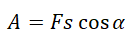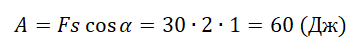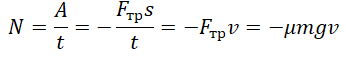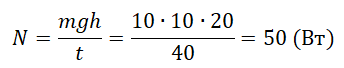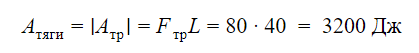Механическая работа что это
Механическая работа и мощность
теория по физике 🧲 законы сохранения
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

Механическая работа совершается, если:
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
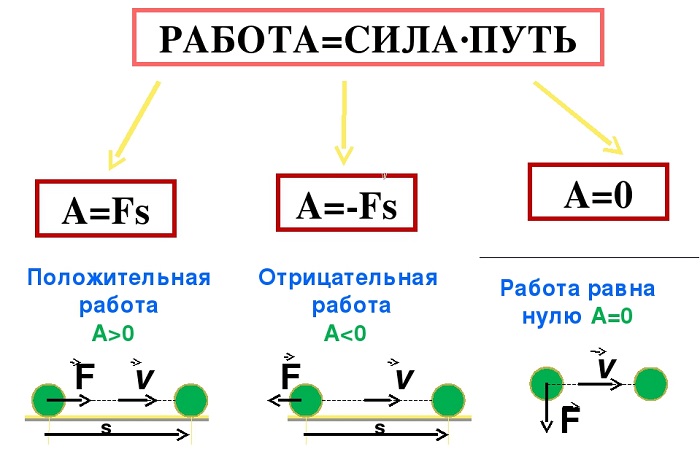
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
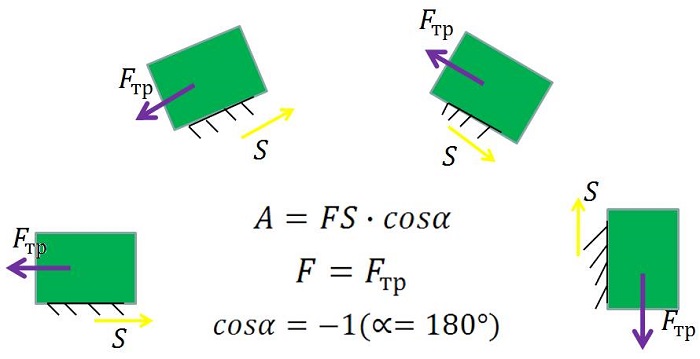
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
Мощность
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела
Работа при равномерном прямолинейном движении определяется формулой:
Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:
Мощность при равномерном подъеме груза
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:
Мгновенная мощность при неравномерном движении
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:
Мощность силы трения при равномерном движении по горизонтали
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство
Работа полезная и полная

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.
Что такое работа в физике – определение и формула
Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию.
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:
В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:
В чем измеряется работа
Физические единицы, в которых выражается механическая работа, – Джоули.
Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах.
Работа силы трения
При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной.
Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.
Положительная и отрицательная работа
Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости.
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей.
Полезная или затраченная работа
У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле.
Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:
КПД = А полезная / А затраченная,
и выражается в процентах. КПД всегда меньше 100.
Мощность
Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:
В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.
Однако при равномерном движении можно использовать и другую формулу:
Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.
Примеры решения задач
Рассмотрим несколько простых задач на нахождение механической работы.
Задача 1
Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.
Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.
При помощи простой математики найдем числовой ответ:
A = 50 м * 10 кг * 10 Н/кг;
Впрочем, не всегда речь идет о силе тяжести.
Задача 2
Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.
Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.
Далее при помощи элементарных вычислений рассчитаем ответ:
A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.
Но во всех задачах по данной теме траектория движения тела прямая.
Задача 3
Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.
В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.
Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.
Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).
F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м =
В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.
Задача 4
Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.
На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы.
Запишем условие в более наглядном виде.
угол A = 150 0 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);
Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).
То есть mg = P * t / КПД.
Шаг 2. P = F * V * cosA.
Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.
V = (m * g * КПД) / (F * t * cosA).
V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);
V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);
Механическая работа
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа
А = FScosα
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
α — угол между векторами силы и перемещения []
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия
Еп = mgh
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
h — высота [м]
На планете Земля g ≈ 9,8 м/с 2
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность
N = A/t
N — мощность [Вт]
A — механическая работа [Дж]
t — время [с]
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность
N = Fv
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность
N = Fvcosα
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
α — угол между векторами силы и скорости []
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
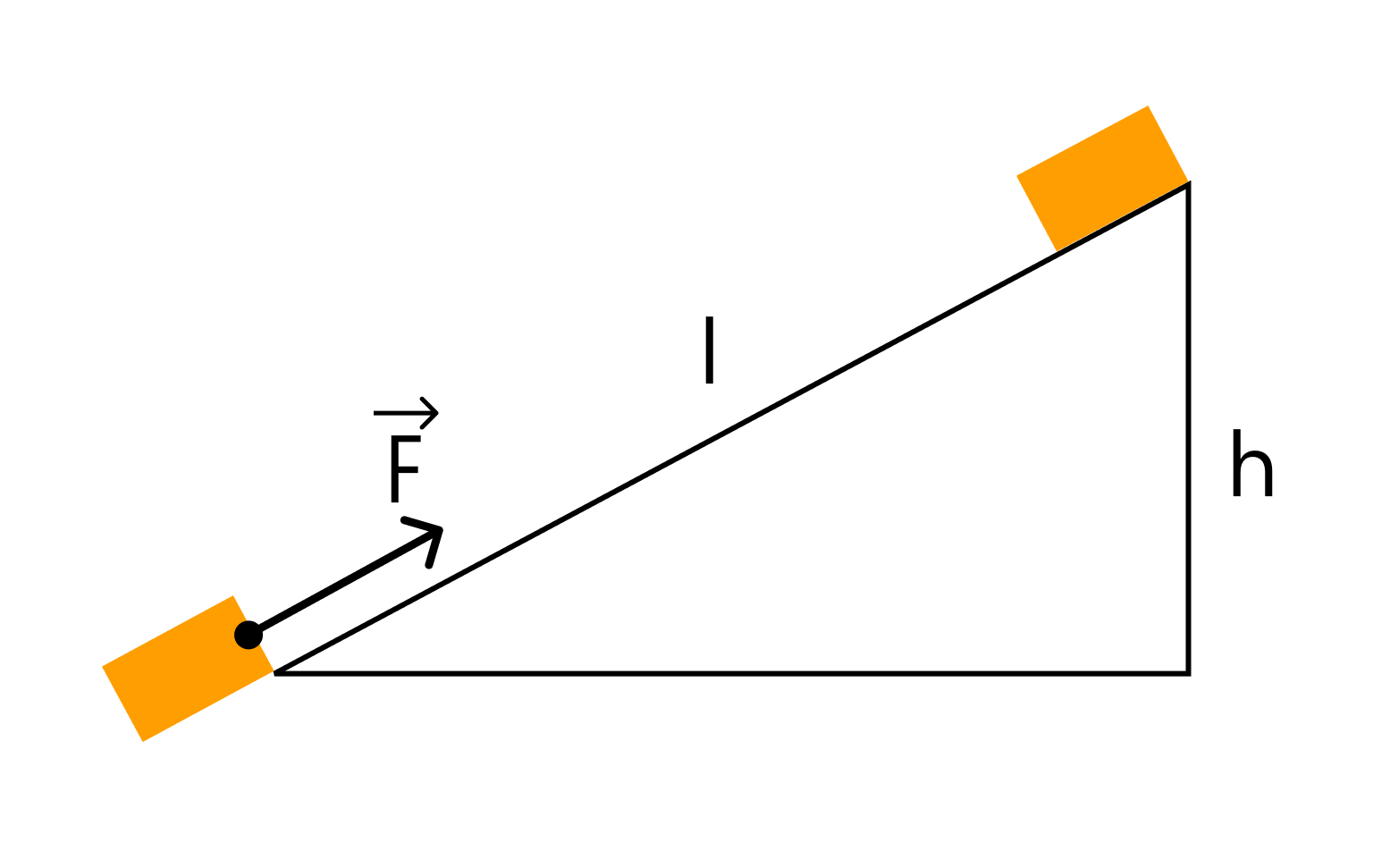
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
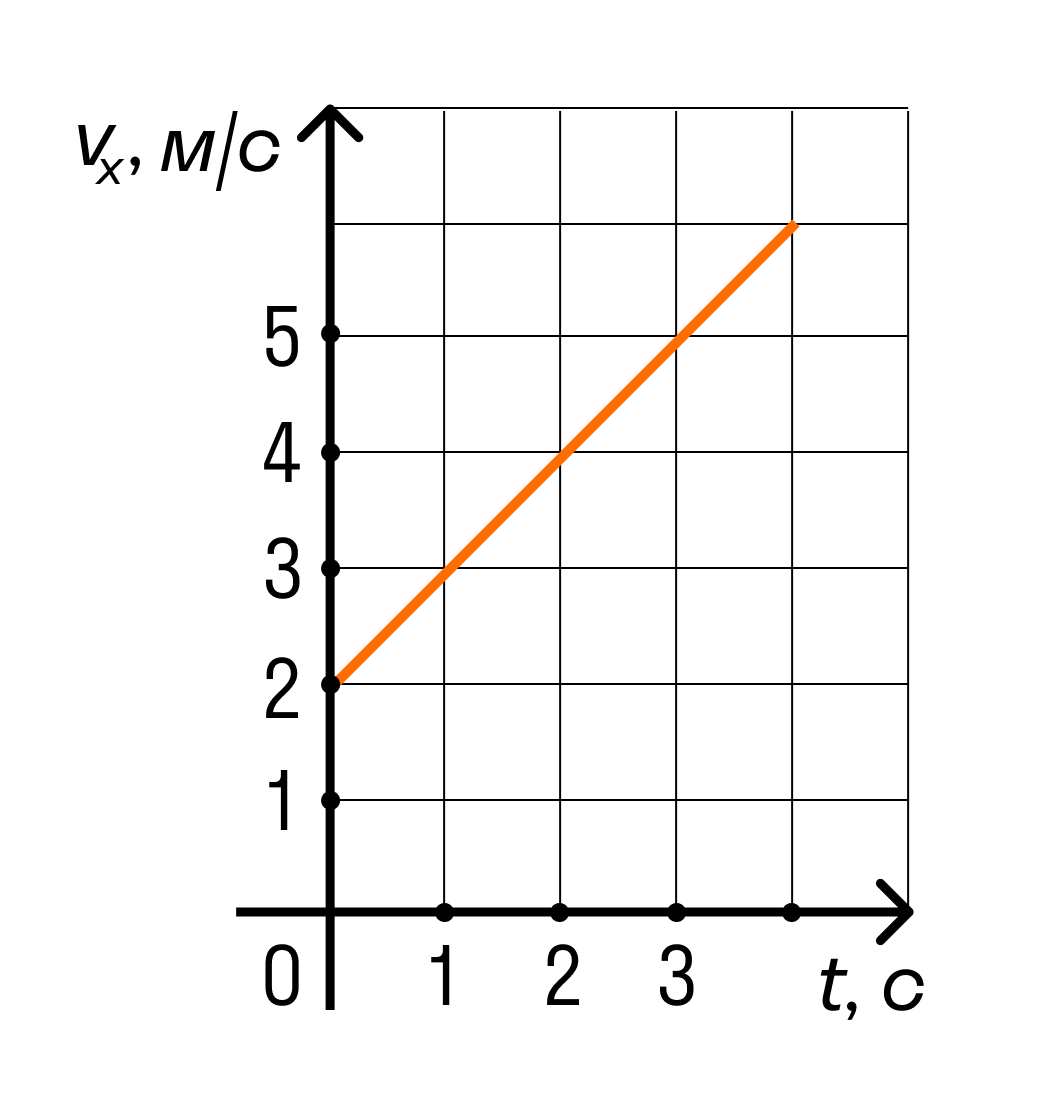
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!