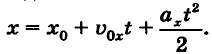Между чем позволяет формализовать функциональные зависимости алгебра
Математические модели
Основным языком информационного моделирования в науке является язык математики.
 Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями. Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями. |
Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении.
Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.

Изменение координаты тела х при прямолинейном равноускоренном движении в любой момент времени t выражается формулой:
С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.

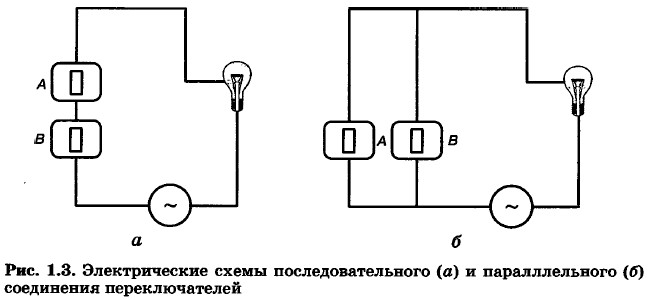
На них изображены известные вам из курса физики последовательное и параллельное соединения переключателеЗ. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателеЗ. Можно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:
Спроектируем электрическую цепь, показывающую итог таЗного голосования комиссии в составе председателя и двух рядовых членов. При голосовании «за» каждыЗ член комиссии нажимает кнопку. Предложение считается принятым, если члены комиссии проголосуют за него единогласно либо если свои голоса «за» отдадут председатель и один из рядовых членов комиссии. В этих случаях загорается лампочка.
Решение. Пусть голосу председателя соответствует переключатель А, голосам рядовых членов — переключатели В и С. Тогда F(A, B,C) = A & B & C ∨ A & B ∨ A & C.
Упростим полученное логическое выражение:
F(A, В, С) = А & В & (С ∨ 1) ∨ A & C = A & B & 1 ∨ A & C = A & B ∨ A & C = A & (B ∨ С).
Мы получили логическую модель, позволяющую построить схему проектируемой электрической цепи, изображённую на рис. 1.4.
§1.2 Знаковые модели
1.2.1. Словесные модели
Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.
Например, гелиоцентрическая модель мира, которую предложил Коперник, словесно описывалась следующим образом:
Множество словесных моделей содержится в ваших школьных учебниках: в учебнике истории представлены модели исторических событий, в учебнике географии — модели географических объектов и природных процессов, в учебнике биологии — модели объектов животного и растительного мира.
Произведения художественной литературы — это тоже модели, так как они фиксируют внимание читателя на определённых сторонах человеческой жизни. Анализируя литературное произведение, вы выделяете в нём объекты и их свойства, отношения между героями, связи между событиями, проводите параллели с другими произведениями и т. п. Самое непосредственное отношение к понятию модели имеет такой литературный жанр, как басня. Смысл этого жанра состоит в переносе отношений между людьми на отношения между вымышленными персонажами, например животными.
Такие особенности естественного языка, как многозначность, использование слов в прямом и переносном значении, синонимия, омонимия и т. п., придают человеческому общению выразительность, эмоциональность, красочность. Вместе с тем наличие этих особенностей делает естественный язык непригодным для создания информационных моделей во многих сферах профессиональной деятельности (например, в системах «человек — компьютер»).
1.2.2. Математические модели
Основным языком информационного моделирования в науке является язык математики.
Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении.
Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.
Модель оптимизации расходов/доходов
С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.
Электрические схемы
1.2.3. Компьютерные математические модели
Многие процессы, происходящие в окружающем нас мире, описываются очень сложными математическими соотношениями (уравнениями, неравенствами, системами уравнений и неравенств). До появления компьютеров, обладающих высокой скоростью вычислений, у человека не было возможности проводить соответствующие вычисления, на счёт «вручную» уходило очень много времени.
В настоящее время самые сложные математические модели могут быть реализованы на компьютере. При этом используются такие средства, как:
— специализированные математические пакеты и программные средства для моделирования.
Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.
Средства компьютерной графики позволяют визуализировать результаты расчётов, получаемых в процессе работы с компьютерными моделями.
Особый интерес для компьютерного математического моделирования представляют сложные системы, элементы которых могут вести себя случайным образом. Примерами таких систем являются многочисленные системы массового обслуживания: билетные кассы, торговые предприятия, ремонтные мастерские, служба скорой помощи, транспортные потоки на городских дорогах и многие другие модели. Многим знакома ситуация, когда, придя в кассу, магазин, парикмахерскую, мы застаём там очередь. Приходится либо вставать в очередь и какое-то время ждать, либо уходить, т. е. покидать систему необслуженным. Возможны случаи, когда заявок на обслуживание в системе мало или совсем нет; в этом случае она работает с недогрузкой или простаивает. В системах массового обслуживания количество заявок на обслуживание, время ожидания и точное время выполнения заявки заранее предсказать нельзя — это случайные величины.
Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.
Имитационное моделирование — это искусственный эксперимент, при котором вместо проведения натурных испытаний с реальным оборудованием проводят опыты с помощью компьютерных моделей. Для получения необходимой информации осуществляется многократный «прогон» моделей со случайными исходными данными, генерируемыми компьютером. В результате образуется такой же набор данных, который можно было бы получить при проведении опытов на реальном оборудовании или в реальной системе. Однако имитационное моделирование на компьютере осуществляется гораздо быстрее и обходится значительно дешевле, чем натурные эксперименты.
Ссылки на ресурсы ЕК ЦОР
Ссылки на ресурсы ФЦИОР:
План-конспект урока по алгебре на тему «Функциональные зависимости и их применение в жизни человека в различных науках» (9 класс)
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
«Функциональные зависимости и их применение в жизни человека и различных науках»
Власенко Лариса Ивановна
Тема и номер урока в теме
Функциональные зависимости и их применение в жизни человека в различных науках. Данный урок является обобщающим в системе уроков по теме «Свойства функций. Квадратичная функция».
Алгебра 9 класс: учебник для общеобразовательных учреждений; Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова.- М.: Просвещение, 2016г.
Цель и задачи урока
Цель: формирование восприятия единства математических моделей и физических процессов как элемента естественнонаучной картины мира.
— обучающие – о бобщить знания о функциях при решении задач из различных областей науки. Привести учащихся к пониманию значения функций в жизни человека. Подготовить учащихся к ГИА по математике, продолжить развитие познавательного интереса к изучению алгебры;
-развивающие — развивать умение анализировать, наблюдать, сопоставлять, логически мыслить; продолжить развитие элементов творческой деятельности учащихся, через вовлечение их в работу частично поискового характера, мотивация учащихся на активный и творческий подход к изучению предметов естественно-математического цикла.
-воспитательные – воспитание навыков коммуникативности в работе, умение слушать и слышать другого; воспитание у учащихся таких нравственных качеств, как аккуратность, инициативность, точность, самостоятельность, активность.
Тип урока – обобщение и систематизация полученных знаний.
Формы работы учащихся – индивидуальная, в парах, фронтальная.
Методы работы- актуализация знаний, самостоятельная работа, использование частично-поискового, исследовательского методов обучения и умение применять полученные знания в измененной ситуации. Также предусмотрена рефлексия.
Необходимое оборудование – компьютер, мультимедиа проектор, раздаточный материал, карточки для самостоятельной работы.
Метапредметность урока позволяет формировать целостное образное видение мира.
Лекция «Моделирование и формализация»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Ссс рииьт ит бим ииииииииииииииииииииимпмитттттттттттттттттттттттттттттттттт м иЛекция «Моделирование и формализация»
Что можно моделировать?
Нас окружает необычайно интересный и сложный мир, познавать который человек начинает с ранних лет.
Детские игрушки похожи на объекты, окружающего мира: людей, животных, автомобили, здания и т. п.
Играя в различные игры, дети воспроизводят отношения, которые складываются в обществе («дочки-матери», «космонавты», «больница» и т. п.)
В своей профессиональной деятельности – научной, практической, художественной – человек также использует модели, т.е. создает образ того объекта (процесса или явления), с которым ему приходится иметь дело.
Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов, зданий, электрических цепей и т. д. Без предварительного создания чертежа невозможно изготовить даже простую деталь, не говоря уже о сложном механизме. В процессе проектирования зданий и сооружений кроме чертежей часто изготавливают макеты. В процессе разработки летательных аппаратов поведение их моделей в воздушных потоках исследуют в аэродинамической трубе.
Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез), отражающих строение, свойства и поведение реальных объектов. Создание новых теоретических моделей иногда коренным образом меняет представление человечества об окружающем мире (гелиоцентрическая система мира Коперника, модель атома Резерфорда-Бора, модель расширяющейся Вселенной, модель генома человека).
Все художественное творчество фактически является процессом создания моделей. Например, такой литературный жанр, как басня, переносит реальные отношения между людьми на отношения между животными и фактически создает модели человеческих отношений.
Какие человеческие отношения смоделировал Крылов, переложив отношения между людьми на животных?
Практически любое литературное произведение может рассматриваться как модель реальной человеческой жизни. Моделями, в художественной форме отражающими реальную действительность, являются также живописные полотна, скульптуры, театральные постановки и т.д.
Что же такое модель?
В реальной жизни этот термин имеет множество значений:
некоторое упрощенное подобие реального объекта;
воспроизведение предмета в уменьшенном или увеличенном виде (макет);
схема, изображение или описание какого-либо явления или процесса в природе и обществе;
новый объект (реальный, информационный или воображаемый), отличный от исходного, который обладает существенными для целей моделирования свойствами и в рамках этих целей полностью заменяет исходный объект.
Модель — материальный объект или образ (мысленный или условный: гипотеза, идея, абстракция, изображение, описание, схема, формула, чертёж, план, карта, блок-схема алгоритма, ноты и т. п.), упрощённо отображающие самые существенные свойства объекта исследования.
Вероятно, первыми моделями, которые замещали реальные объекты, были языковые знаки. Они возникли в ходе развития человечества и постепенно превратились в разговорный язык. Первые наскальные рисунки (петроглифы), имеющие возраст в 200 тысяч лет, были графическими моделями, которые изображали бытовые сцены, животных и сцены охоты. Следующим этапом развития моделирования можно считать возникновение систем счисления и числовых знаков.
Моделирование получило развитие ещё в Древней Греции. В V—III вв. до н. э Птолемей создал геометрическую модель Солнечной системы, а Гиппократ использовал для изучения строения глаза человек глаз быка (как физическую модель глаза).
Зачем создаются модели?
Строгие правила построения моделей сформулировать невозможно, однако человечество накопило богатый опыт моделирования различных объектов и процессов.
При построении модели необходимо учитывать
Рассмотрим несколько примеров моделей, созданных с разной целью:
· тренажер, для обучения управлением самолетом;
· манекен для примерки одежды;
· план Московского Кремля
Попробуйте сами определить, для какой цели была создана каждая из перечисленных моделей, и кому она может быть полезна?
Как видно из примеров, человек создает модели объектов, которые позволяют решать самые разнообразные задачи:
· создание объектов с заданными свойствами;
· объяснение известных фактов;
· получение новых знаний об исследуемых объектах;
В процессе построения модели выделяются главные, наиболее существенные для проводимого исследования свойства.
Например : В процессе исследования аэродинамических качеств модели самолета в аэродинамической трубе важно, чтобы модель имела геометрическое подобие оригинала, но не важен, например, ее цвет.
Разные науки исследуют объекты и процессы под разными углами зрения и строят различные типы моделей. В физике изучаются процессы взаимодействия и изменения объектов, в химии — их химический состав, в биологии — строение и поведение живых организмов и так далее.
Возьмем в качестве примера человека: в разных науках он исследуется в рамках различных моделей. В рамках механики его можно рассматривать как материальную точку, в химии — как объект, состоящий из различных химических веществ, в биологии — как систему, стремящуюся к самосохранению.
Достоинствами метода моделирования являются:
меньшая продолжительность во времени (например, для экономических моделей).
трудности построения адекватной модели;
сбор большого количества достоверной информации.
Термин «адекватность» (происходит от лат. adaequatus — «приравненный, равный») означает верное воспроизведение в модели связей и отношений объективного мира. Этим термином характеризуется качество созданной модели.
Адекватность теоретических моделей законам реального мира проверяется с помощью опытов и экспериментов.
С другой стороны, разные объекты могут описываться одной моделью. Так, в механике различные материальные тела (от планеты до песчинки) могут рассматриваться как материальные точки.
Признаки классификаций моделей:
1) Классификация моделей по области использования:
Учебные модели – используются при обучении. Это могут быть наглядные пособия, различные тренажеры, обучающие программы.
Опытные модели – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик.
Например, модель корабля исследуется в бассейне для изучения устойчивости судна при качке, модель автомобиля «продувается» в аэродинамической трубе с целью исследования обтекаемости кузова, модель сооружения используется для привязки здания к конкретной местности и т.д.
Игровые модел и – это военные, экономические, спортивные, деловые игры. Эти модели как бы репетируют поведение объекта в различных ситуациях, проигрывая их с учетом возможной реакции со стороны конкурента, союзника или противника. С помощью игровых моделей можно оказывать психологическую помощь больным, разрешать конфликтные ситуации.
Имитационные модели непросто отражают реальность с той или иной степенью точности, а имитируют ее. Эксперименты с моделей проводят при разных исходных данных. По результатам исследования делаются выводы. Такой метод подбора правильного решения получил название (метод проб и ошибок). Например, для выявления побочных действий лекарственных препаратов их испытывают в серии опытов над животными.
2) Классификация моделей по фактору времени:
Статические – модели, описывающие состояние системы в определенный момент времени (единовременный срез информации по данному объекту). Например, обследование учащихся в стоматологической поликлинике дает состояние их зубов в данный момент времени: соотношение молочных и постоянных, наличие пломб, дефектов и т.п.
Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени). Примеры: описание движения тел, развития организмов, процесс химических реакций.
При строительстве дома рассчитывают прочность его фундамента, стен, балок и устойчивость их к постоянной нагрузке. Это статическая модель здания. Но надо так же обеспечить противодействие ветрам, движению грунтовых вод, сейсмическим колебаниям и другим изменяющимся во времени факторам. Эти вопросы можно решить с помощью динамических моделей.
Таким образом, один и тот же объект можно охарактеризовать и статической и динамической моделью.
3) Классификация моделей по отрасли знаний
— это классификация по отрасли деятельности человека: математические, биологические, химические, социальные, экономические, исторические и т.д.
4) Классификация моделей по форме представления:
Материальные (предметные) модели всегда имеют реальное воплощение. Они отражают внешнее свойство и внутреннее устройство исходных объектов, суть процессов и явлений объекта-оригинала. Это экспериментальный метод познания окружающей среды. Примеры: детские игрушки, скелет человека, чучело, макет солнечной системы, школьные пособия, физические и химические опыты.
Информационные модели – целенаправленно отобранная информация об объекте, которая отражает наиболее существенные для исследователя свойства этого объекта.
Образные модели (рисунки, фотографии и др.) представляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (бумаге, фото- и кинопленке и др.). Широко используются образные информационные модели в образовании (вспомните учебные плакаты по различным предметам) и науках, где требуется классификация объектов по их внешним признакам (в ботанике, биологии, палеонтологии и др.).
В 
— Земля вращается вокруг Солнца, а Луна вращается вокруг Земли;
— все планеты вращаются вокруг Солнца.
Однако более нагляден способ ее представления в виде рисунка
В химии строение молекулы воды можно качественно описать на естественном языке:
«Молекула воды состоит из атома кислорода и двух атомов водорода».
Для наглядности строение молекулы можно нарисовать.
Ярким примером образной модели является географическая карта. Цвет и форма материков, океанов, гор, изображенных на карте, сразу подключает образное мышление. По цвету на карте сразу можно оценить рельеф. Например, с голубым цветом у человека ассоциируется вода, с зеленым цветущий луг, равнина. Карта изобилует условными обозначениями. Зная этот язык, человек может получить достоверную информацию об интересующем его объекте. Информационная модель в этом случае будет результатом осмысления сведений, полученных при помощи органов чувств и информации, закодированной в виде условных изображений.
То же можно сказать о живописи. Неискушенный зритель воспримет картину душой в виде образной модели. Но существуют некоторые художественные языки, соответствующие различным живописным жанрам и школам: сочетание цветов, характер мазка, способы передачи воздуха, объема и т. д. Человеку, знающему эти условности, легче разобраться в том, что имел в виду художник, особенно если произведение не относится к реализму. При этом общее восприятие картины (информационная модель) станет результатом осмысления информации как в образной, так и в знаковой формах.
Еще один пример такой модели — фотография. Фотоаппарат позволяет получить изображение оригинала. Обычно фотография дает нам довольно точное представление о внешнем облике человека. Существуют некоторые признаки (высота лба, посадка глаз форма подбородка), по которым специалисты могут определить характер человека, его склонность к тем или иным поступкам. Этот специальный язык формируется из сведений, накопленных в области физиогномики и собственного опыта. Знающие врачи, взглянув на фото незнакомого человека, увидят признаки некоторых заболеваний. Задавшись разными целями, по одной и той же фотографии можно получить различные информационные модели. Они будут результатом обработки образной информации, полученной при разглядывании фотографии, и информации, сложившейся на основе знания специального профессионального языка.
Знаковые информационные модели строятся с использованием различных языков (знаковых систем). Знаковая информационная модель может быть представлена в форме текста (например, программы на языке программирования), формулы (например, второго закона Ньютона F = m × а), таблицы (например, периодической таблицы элементов Д. И. Менделеева) и так далее.
Иногда при построении знаковых информационных моделей используются одновременно несколько различных языков. Примерами таких моделей могут служить географические карты, графики, диаграммы и пр. Во всех этих моделях используются одновременно как язык графических элементов, так и символьный язык.
На протяжении своей истории человечество использовало различные способы и инструменты для создания информационных моделей. Эти способы постоянно совершенствовались. Так, первые информационные модели создавались в форме наскальных рисунков, в настоящее же время информационные модели обычно строятся и исследуются с использованием современных компьютерных технологий.
Язык алгебры позволяет формализовать функциональные зависимости между величинами. Так, Ньютон формализовал гелиоцентрическую систему мира, открыв законы механики и закон всемирного тяготения и записав их в виде алгебраических функциональных зависимостей. В школьном курсе физики рассматривается много разнообразных функциональных зависимостей, выраженных на языке алгебры, которые представляют собой математические модели изучаемых явлений или процессов.
В процессе познания окружающего мира человечество постоянно использует моделирование и формализацию. При изучении нового объекта сначала обычно строится его описательная информационная модель на естественном языке, затем она формализуется, то есть выражается с использованием формальных языков (математики, логики и др.).
Визуализация формальных моделей
Так при визуализации формальных физических моделей с помощью анимации может отображаться динамика процесса, производиться построение графиков изменения физических величин и так далее. Визуальные модели обычно являются интерактивными, то есть исследователь может менять начальные условия и параметры протекания процессов и наблюдать изменения в поведении модели.
В настоящее время широкое распространение получили компьютерные интерактивные визуальные модели. В таких моделях исследователь может менять начальные условия и параметры протекания процессов и наблюдать изменения в поведении модели.