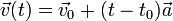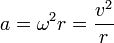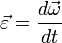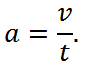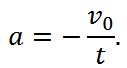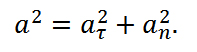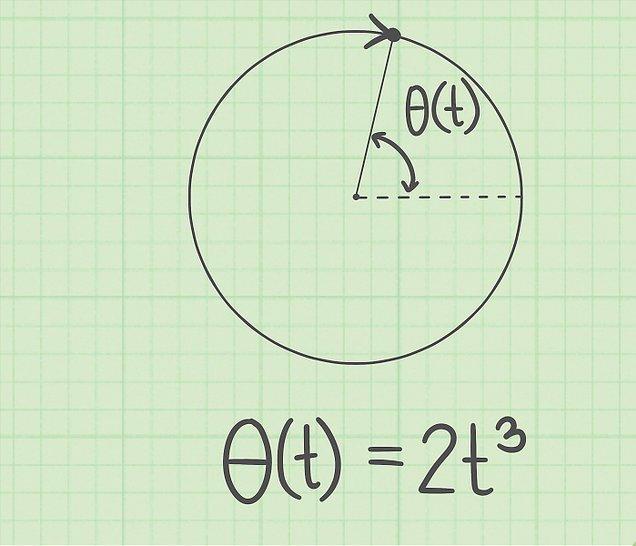Мгновенное ускорение в чем измеряется
Что такое ускорение?
Ускорение — физическая векторная величина, которая характеризует насколько быстро тело (материальная точка) изменяет скорость своего движения. Ускорение является важной кинематической характеристикой материальной точки.
Самый простой вид движения — равномерное движение по прямой линии, когда скорость тела постоянна и тело за любые равные промежутки времени проходит одинаковый путь.
Но большинство движений неравномерны. На одних участках скорость тела больше, на других меньше. Машина начиная движение двигается все быстрее. а останавливаясь замедляется.
Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным.
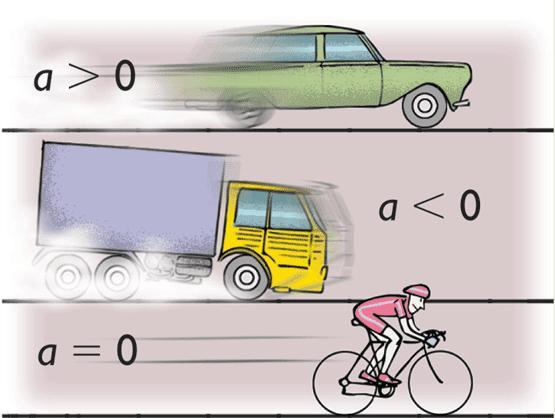
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
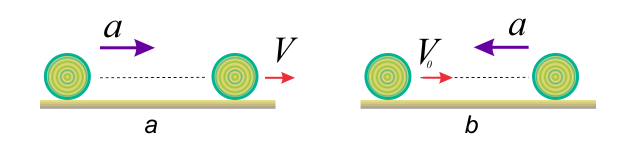
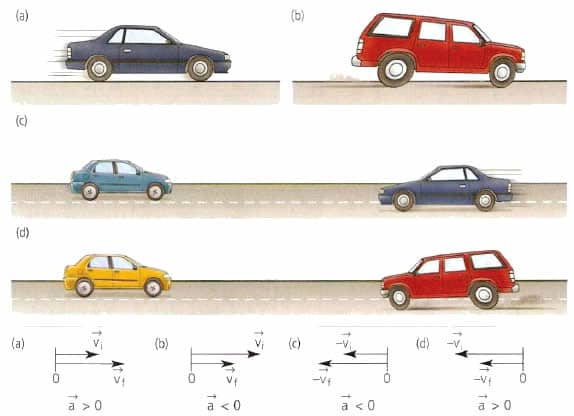
Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость (рис. а); если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону (рис. б).
Среднее и мгновенное ускорение
Среднее ускорение материальной точки на некотором промежутке времени — это отношение изменения его скорости, что произошло за это время, к продолжительности этого промежутка:
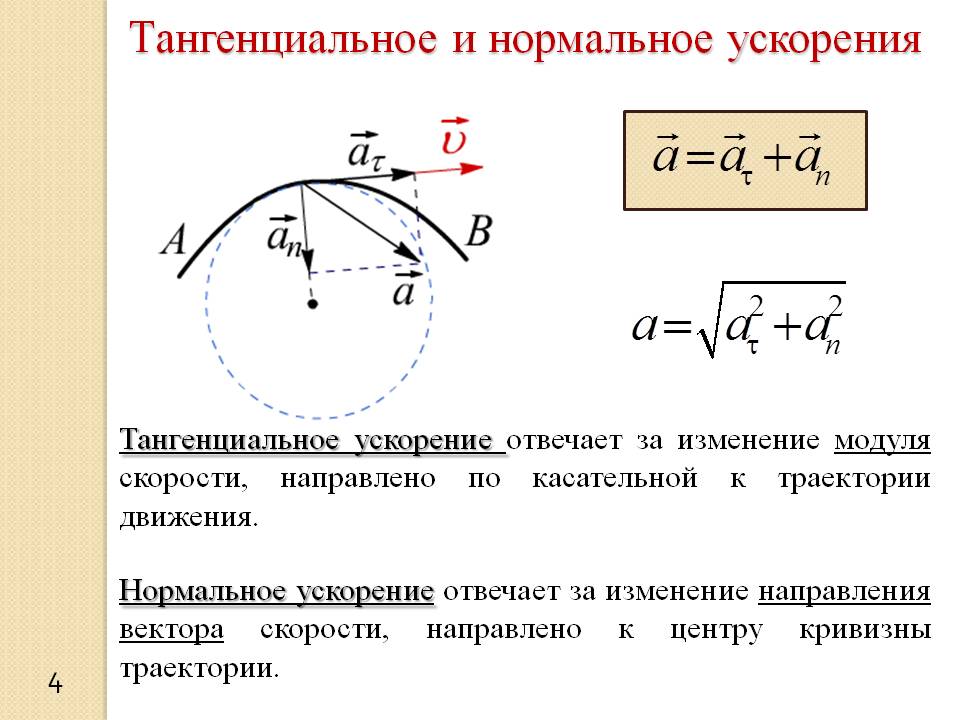
Тангенциальное и нормальное ускорение
\( = \dfrac
где \( \theta \) — угол между вектором скорости и осью абсцисс; \( \hat n \) — орт перпендикуляра к скорости.
где \( \vec a_ <\tau>= \dfrac
Учитывая, что вектор скорости направлен по касательной к траектории движения, то \( \hat n \) — это орт нормали к траектории движения, который направлен к центру кривизны траектории. Таким образом, нормальное ускорение направлено к центру кривизны траектории, в то время как тангенциальное — по касательной к ней. Тангенциальное ускорение характеризует скорость изменения величины скорости, в то время как нормальное характеризует скорость изменения ее направления.
\( a_
Измерение ускорения
Ускорение измеряется в метрах (разделенных) на секунду во второй степени (м/с 2 ). Величина ускорения определяет, насколько изменится скорость тела за единицу времени, если оно будет постоянно двигаться с таким ускорением. Например, тело, движущееся с ускорением 1 м/с 2 за каждую секунду изменяет свою скорость на 1 м/с.
Мгновенное ускорение и скорость в физике
Мгновенная скорость в физике
Мгновенной скоростью называется скорость объекта в данный момент времени в конкретной точке. Это векторная физическая величина, которая обозначается символом \vec v и определяется по формуле:
Где \(\Delta\vec S\) — перемещение, а \(\Delta t \) — промежуток времени.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Величина измеряется в м/с.
Мгновенное ускорение в физике
Мгновенное ускорение — это векторная физическая величина, численно равная изменению скорости в единицу времени.
Как направлены мгновенная скорость и ускорение
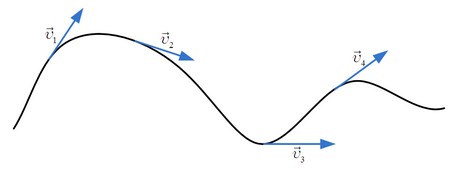
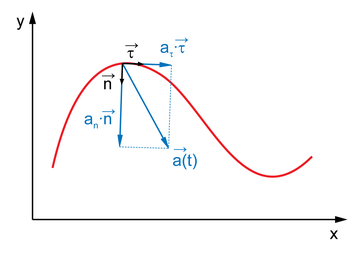
Вектор мгновенной скорости всегда направлен по касательной к траектории движения объекта в любой момент времени. Графически это выглядит так:
У вектора \vec a две составляющие: \(\vec a_tg\) (касательное или тангенциальное \(\vec a\) ) и \(\vec a_n\) (нормальное \(\vec a\) ). Каждая из них имеет свое направление вектора.
Как найти мгновенное ускорение, формула
Ускорение определяется по формуле:
Где \(\Delta\vec V\) — изменение скорости, \(\Delta t\) — промежуток времени, когда происходило изменение скорости.
Составляющими данной векторной величины являются:
Касательное — указывает, насколько быстро изменяется скорость объекта по модулю. Оно вычисляется по формуле:
Вектор тангенциального ускорения направлен по касательной к траектории движения тела.
Нормальное — характеризует быстроту изменения скорости по направлению и всегда направлено к центру кривизны траектории. Определяется по формуле:
Задача на определение мгновенного ускорения
Для усвоения теоретического материала важно закрепить знания на практике. Решим задачу на определение мгновенного ускорения.
Задача
С каким ускорением движется гоночный болид, если его скорость изменилась со 144 км/ч до 216 км/ч за 6 секунд?
Записываем все известные вводные:
\(V_0\) =144 км/ч, \(V\) =216 км/ч, t=6 с, a=?
Переводим км/ч в м/с, получаем:
Где \(\Delta\vec V=V-V_0\)
Мгновенное ускорение
Ускоре́ние (обычно обозначается 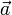
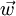
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Раздел механики, изучающий движение в трёхмерном евклидовом пространстве, его запись, а также запись скоростей и ускорений в различных системах отсчёта, называется кинематикой.
Производная ускорения по времени т.е. величина, характеризующая быстроту изменения ускорения по времени называется рывок.
Содержание
Кинематика точки
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости частицы по времени:
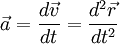
Ускорение точки при прямолинейном движении
Если вектор 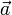
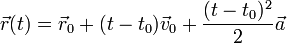
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю во всё время движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), так что говорят, что движение прямолинейно и равномерно.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное не верно.)
Ускорение точки при движении по окружности
Если точка движется по окружности с постоянной по модулю скоростью, ее ускорение все равно не равно 0, поскольку направление вектора скорости постоянно изменяется. Ускорение в этом случае называется центростремительным, посколку его вектор всегда направлен к центру окружности, а его модуль равен:
Если при движении по окружности модуль скорости изменяется, удобно ввести такое понятие, как угловое ускорение, аналогичное угловой скорости. Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растет, и наоборот.
Ускорение точки при движении по кривой
Вектор ускорения 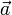
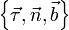
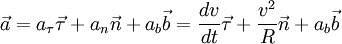
Известно, что 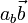
Векторы 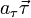
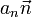
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
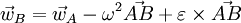
где 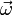
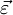
Второе слагаемое называется центростремительным ускорением.
Ускорение при сложном движении
Абсолютное ускорение равно сумме относительно, переносного и кориолисова:
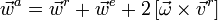
Динамика точки
Первый закон Ньютона постулирует существование инерциальных систем отсчета. В этих системах отсчета равномерное прямолинейное движение имеет место всякий раз, когда материальная точка (но не тело!) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчета всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что приложенная (к точке) сила и порождаемое ей ускорение точки всегда пропорциональны, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
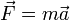
Единицы измерения ускорения
См. также
Ссылки
Полезное
Смотреть что такое «Мгновенное ускорение» в других словарях:
мгновенное ускорение — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN instantaneous acceleration … Справочник технического переводчика
мгновенное ускорение — akimirkinis pagreitis statusas T sritis Standartizacija ir metrologija apibrėžtis Kūno pagreitis tam tikrą akimirką. atitikmenys: angl. instantaneous acceleration vok. Momentanbeschleunigung, f; momentane Beschleunigung, f rus. мгновенное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
мгновенное ускорение — akimirkinis pagreitis statusas T sritis fizika atitikmenys: angl. instantaneous acceleration vok. Momentanbeschleunigung, f; momentane Beschleunigung, f rus. мгновенное ускорение, n pranc. accélération instantanée, f … Fizikos terminų žodynas
УСКОРЕНИЕ — (1) материальной точки векторная величина а, характеризующая быстроту изменения с течением времени вектора скорости v (см. (1)) точки: Согласно второму закону Ньютона (см.), ускорение прямо пропорционально результирующей механической силе F,… … Большая политехническая энциклопедия
Дельта-функция — У этого термина существуют и другие значения, см. Дельта (значения). Схематический график одномерной дельта функции. Дельта функция (или … Википедия
Δ-функция — (или дельта функция, δ функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или… … Википедия
Дельта-функция Дирака — δ функция (или дельта функция, δ функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или… … Википедия
Дельта функция — δ функция (или дельта функция, δ функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или… … Википедия
Импульсная функция — δ функция (или дельта функция, δ функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или… … Википедия
Функция Дирака — δ функция (или дельта функция, δ функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или… … Википедия
Единицы измерения ускорения.
Ускорение – это физическая величина (a, от лат. acceleratio), характеризующая быстроту изменения скорости тела. Ускорение является векторной величиной, показывающей, насколько изменяется вектор скорости 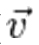
Рассмотрим движение автомобиля. Трогаясь с места, он увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус.
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ 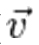
Равнопеременное движение точки – это движение с постоянным ускорением,
Под словом равнопеременное понимают:
2. Равнозамедленное движение – если модуль скорости уменьшается, т.е. ускорение антипараллельно скорости: 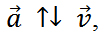
Поскольку ускорение равнопеременного движения постоянно, оно равно изменению скорости за любой конечный интервал времени:
где 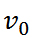
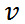

Если же нулю равна не начальная, а конечная скорость ( 
При движении по криволинейной траектории изменяется не только модуль скорости, но и ее направление. В этом случае вектор ускорения представляют в виде двух составляющих: тангенциальной – по касательной к траектории движения, и нормальной – перпендикулярно траектории
В соответствии с этим проекцию ускорения 
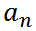
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Направление вектора тангенциального ускорения 
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть, вектор нормального ускорения перпендикулярен линейной скорости движения. Нормальное ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

Среднее и мгновенное ускорение и скорость. Формулы. Пример задачи
В физике рассмотрением особенностей движения макроскопических твердых тел занимается кинематика. Этот раздел механики оперирует такими понятиями, как скорость, ускорение и путь. В данной статье мы сосредоточим свое внимание на вопросах, что такое мгновенное ускорение и скорость. Также рассмотрим, какими формулами можно определить эти величины.
Нахождение скорости
Об этом понятии известно каждому школьнику, начиная уже с младших классов. Все ученики знакомы с приведенной ниже формулой:
В старших классах школ скорость, как физическая величина, рассматривается в новом свете. Ученикам предлагают следующее ее определение:
Ускорение
Благодаря этому равенству можно определить изменение величины v в любой точке траектории.
По аналогии со скоростью, среднее ускорение вычисляется по такой формуле:
Движение с постоянным ускорением
Отличительной особенностью этого типа перемещения тел в пространстве является постоянство величины а, то есть a=const.
Это движение также называют равноускоренным или равнозамедленным в зависимости от взаимного направления векторов скорости и ускорения. Ниже такое перемещение рассмотрим на примере двух наиболее распространенных траекторий: прямой линии и окружности.
При перемещении по прямой линии во время равноускоренного движения мгновенная скорость и ускорение, а также величина пройденного пути, связаны следующими равенствами:
Что касается скорости, то первое выражение позволяет определить ее в любой момент времени. То есть это будет мгновенный показатель. Для расчета средней скорости необходимо воспользоваться представленным выше выражением, то есть:
v = S/t = v0 ± a*(t1 + t2)/2.
При изучении движения по окружности с постоянным ускорением в физике используют угловые характеристики, которые аналогичны соответствующим линейным. К ним относится угол поворота θ, угловая скорость и ускорение (ω и α). Эти величины связаны в равенства, аналогичные выражениям равноускоренного движения по прямой линии, которые приводятся ниже:
При этом угловые характеристики связаны с линейными следующим образом:
Задача на определение среднего и мгновенного ускорения
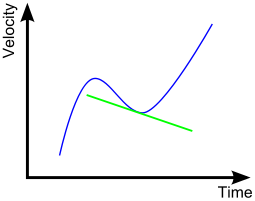
Известно, что тело движется по сложной траектории. Его мгновенная скорость меняется по времени следующим образом:
Чему равно мгновенное ускорение тела в момент t=3 (секунды)? Найти среднее ускорение за промежуток времени от двух до четырех секунд.
На первый вопрос задачи ответить несложно, если вычислить производную от функции v(t). Получаем:
Для определения среднего ускорения, следует воспользоваться таким выражением:
Из расчетов следует, что среднее ускорение немного превышает мгновенное в середине рассмотренного временного промежутка.