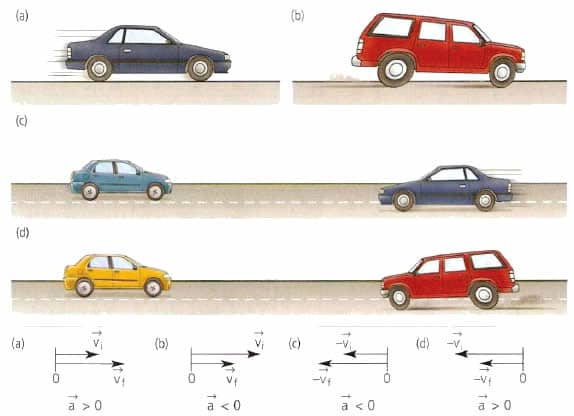
Мгновенную скорость можно рассчитывать по той же формуле что и среднюю

Среднее и мгновенное ускорение и скорость. Формулы. Пример задачи

В физике рассмотрением особенностей движения макроскопических твердых тел занимается кинематика. Этот раздел механики оперирует такими понятиями, как скорость, ускорение и путь. В данной статье мы сосредоточим свое внимание на вопросах, что такое мгновенное ускорение и скорость. Также рассмотрим, какими формулами можно определить эти величины.

Нахождение скорости

Об этом понятии известно каждому школьнику, начиная уже с младших классов. Все ученики знакомы с приведенной ниже формулой:

Вам будет интересно: Геохимический барьер: определение термина, особенности

В старших классах школ скорость, как физическая величина, рассматривается в новом свете. Ученикам предлагают следующее ее определение:

Ускорение

Благодаря этому равенству можно определить изменение величины v в любой точке траектории.

По аналогии со скоростью, среднее ускорение вычисляется по такой формуле:

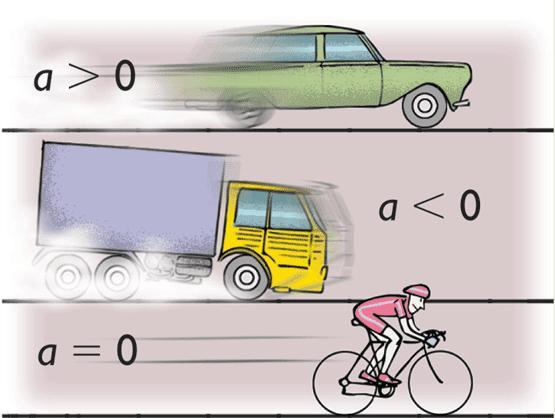
Движение с постоянным ускорением

Отличительной особенностью этого типа перемещения тел в пространстве является постоянство величины а, то есть a=const.

Это движение также называют равноускоренным или равнозамедленным в зависимости от взаимного направления векторов скорости и ускорения. Ниже такое перемещение рассмотрим на примере двух наиболее распространенных траекторий: прямой линии и окружности.

При перемещении по прямой линии во время равноускоренного движения мгновенная скорость и ускорение, а также величина пройденного пути, связаны следующими равенствами:

Что касается скорости, то первое выражение позволяет определить ее в любой момент времени. То есть это будет мгновенный показатель. Для расчета средней скорости необходимо воспользоваться представленным выше выражением, то есть:

v = S/t = v0 ± a*(t1 + t2)/2.

При изучении движения по окружности с постоянным ускорением в физике используют угловые характеристики, которые аналогичны соответствующим линейным. К ним относится угол поворота θ, угловая скорость и ускорение (ω и α). Эти величины связаны в равенства, аналогичные выражениям равноускоренного движения по прямой линии, которые приводятся ниже:

При этом угловые характеристики связаны с линейными следующим образом:

Задача на определение среднего и мгновенного ускорения

Известно, что тело движется по сложной траектории. Его мгновенная скорость меняется по времени следующим образом:

Чему равно мгновенное ускорение тела в момент t=3 (секунды)? Найти среднее ускорение за промежуток времени от двух до четырех секунд.

На первый вопрос задачи ответить несложно, если вычислить производную от функции v(t). Получаем:

Для определения среднего ускорения, следует воспользоваться таким выражением:

Из расчетов следует, что среднее ускорение немного превышает мгновенное в середине рассмотренного временного промежутка.

Источник

Формула скорости — обозначение, единицы измерения и примеры нахождения

Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Источник

Физика

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Закон сложения скоростей

Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена (см. рисунок 1).

Рисунок 1 – Первоначальная скорость пчелы и ветра

Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):

Рисунок 2 – Изменившаяся скорость пчелы

Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v₂ системе отсчета.

Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре

Мгновенная скорость, направление мгновенной скорости

Средняя скорость. Средняя путевая скорость

Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.

Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.

Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:

Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.

То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.

Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt₁, Δt₂,…Δt_n, и найти средние скорости за эти отрезки времени:

А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δt_b направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.

Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:

Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.

Ускорение. Касательное ускорение. Центростремительное ускорение

Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.

Единицы измерения ускорения:

Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.

Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2

Равноускоренное движение

Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении

Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:

Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.

При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:

Если же ускорение противонаправлено начальной скорости, это выражение станет таким:

Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении

Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.

Свободное падение

Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение

Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.

Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).

Рисунок 9 – Свободное падение тела

Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:

Представим, что тело подкинули вертикально наверх с начальной скоростью v₀ (см. рисунок 10).

Рисунок 10 – Тело бросили вертикально вверх

Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v₀ (вообще нужно было бы писать v_oy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).

Отсюда можно найти полное время полета:

Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.

Рисунок 11 – Тело брошено под углом к горизонту

Уравнения движения в общем виде по двум осям выглядят так:

Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:

Равномерное движение точки по окружности

Центростремительное ускорение

Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).

Рисунок 12 – Изменение направления скорости при равномерном движении по окружности

За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:

где R – радиус окружности, по которой циклически движется тело.

Источник

Мгновенную скорость можно рассчитывать по той же формуле что и среднюю

Если взять длину отрезка пути, пройденного телом, измеренного в метрах, (в нашем случае, для простоты, «материальной точкой». То есть телом, размерами которого можно пренебречь в данной конкретной задаче) и разделить на время, затраченное на прохождение этого отрезка пути в секундах, то полученная величина будет являться «средней скоростью» тела на данном отрезке пути.

Почему средней, надеюсь, понятно?

Соответственно, если мы рассмотрим отрезок пути произвольно движущегося тела и отсечем время, за которое это тело преодолеет данный участок пути, а потом разделим на это время длину отрезка пути, то получим некую величину с размерностью скорости. Метры в секунду.

Черточка над v означает, что это средняя скорость.

Если мы рассмотрим две половины данного отрезка и, соответственно два времени прохождения этих отрезков телом, то мы получим две скорости (средние скорости на каждом отрезке), которые в реальном движении не будут равны между собой и не будут равны средней скорости на целом отрезке. При этом, заметим, что сумма двух половин отрезка пути равна длине всего отрезка, а сумма времен равна времени прохождения всего отрезка.

Сравнив их, мы сможем сделать выводы на каком участке тело двигалось быстрее, а на каком медленнее.

Теперь представим себе, что мы разделили наш целый отрезок пути на бесконечно маленькие отрезки и измерили время прохождения каждого бесконечно маленького отрезка, а, затем, разделили путь на время на каждом бесконечно малом отрезке.

Что мы получим в результате?

Бесконечно малый отрезок считаем точкой.

Разберемся в этом подробнее.

Представить себе деление бесконечно малого расстояния на бесконечно малое время (Подумайте сами, почему время тоже бесконечно малое!) не очень то легко.

Это очень просто представить, как процесс, изображенный на рисунке 3. Возьмем какой-либо маленький отрезок (отрезок пути в смысле рассматриваемой нами задачи) и разделим его на время прохождения нашим телом этого отрезка. Получим среднюю скорость тела на этом отрезке. Это мы уже знаем.

А дальше продолжим этот процесс много-много раз. Одна восьмая, одна шестнадцатая, одна тридцать вторая, одна шестьдесят четвертая, и т.д. Нужно отметить, что мы очень быстро будем брать в рассмотрение настолько маленькие отрезки, что средняя скорость на этих все меньших и меньших отрезках с какого-то момента перестанет в наших измерениях меняться.

. В реальном эксперименте мы можем остановить наш процесс по нескольким причинам.

Может оказаться, что после какого-то очередного деления отрезка и измерения средняя скорость тела в каждом последующем измерении (на каждом последующем отрезке, в качестве которого мы берем первую половину предыдущего отрезка) после каждого очередного деления перестанет изменяться с точностью до нужного количества знаков после запятой.

В этом случае мы можем договориться (сами с собой), что наш процесс можно остановить, а полученную величину считать мгновенной скоростью в точке начала нашего первого отрезка пути.

. При этом мы производим допущение, что дальнейший (бесконечный) процесс деления отрезков и измерения средних скоростей на их первых половинках (половинках, примыкающих к началу первого отрезка пути) не приведет к изменению значения средних скоростей с требуемой нами точностью.

По сути, мы заменили бесконечный процесс конечным алгоритмом действий.

Таким образом, мы договариваемся считать результат этого вышеописанного конечного процесса равным результату деления бесконечно малого отрезка пути на бесконечно малое время прохождения этого отрезка телом.

В строгом математическом виде пишется:

Читается: «предел функции при стремящемся к нулю».

Эту величину мы пока условимся называть «мгновенной скоростью тела в точке».

Но процесс вычисления мгновенной скорости можно себе представить и по-другому. Мы делили на отрезки путь. А можно делить отрезок времени. И это будет правильно с точки зрения физики. Делить, все ближе и ближе приближаясь к моменту времени, для которого мы хотим определить мгновенную скорость.

А теперь устремляем наш отрезок времени к нулю. Т.е. делаем его все меньше и меньше (главное, чтобы наша точка, в которой вычисляем мгновенную скорость всегда была в пределах этого отрезка, например, в начале). Еще меньше. И еще меньше!

Насколько меньше? Очень, очень, очень маленьким! Бесконечно малым.

Это очень просто определить чисто математически: «Бесконечно малая величина – это величина меньшая, чем любая, сколь угодно малая конечная величина». Что это означает?

Очень просто. Берем любой самый маленький конечный отрезок времени. Его можно записать в виде числа секунд, например. Одна миллисекунда – это одна тысячная секунды. Наш бесконечно малый отрезок строго меньше одной миллисекунды. И одной миллиардной секунды (микросекунды). И одной наносекунды! И вообще, если даже мы напишем на большой стене число с миллионами нулей после запятой, то и тогда наша бесконечно малая величина будет строго меньше!

Обозначается бесконечно маленький отрезок времени dt (маленькая латинская буква d вместо ∆ , которая обычно означает конечность отрезка). Догадайтесь самостоятельно, почему отрезок пути, пройденный телом за бесконечно малый отрезок времени, тоже бесконечно малый! Операция деления бесконечно малого отрезка пути на бесконечно малый отрезок времени записывается

Если у нас есть функция зависимости координаты от времени X ( t ), то проделав для каждого значения t операцию нахождения мгновенной скорости, мы получим функцию V ( t ) – функцию зависимости мгновенной скорости тела от времени. Математически мы запишем формулу

Договоримся в нашей книге обозначать производную по времени точкой, а производные по другим величинам, кроме времени штрихом!

Возникает вопрос, а зачем мы все это записали, если мы все равно не сможем повторить операцию нахождения мгновенной скорости для каждой точки – их же бесконечное количество?

Например, пусть мы знаем зависимость координаты от времени

Тогда мы можем тут же вычислить зависимости скорости

Это круто! Потому, что если нам известна функция зависимости координаты от времени, находя производную этой функции по времени, мы сразу же узнаем мгновенную скорость в каждый момент времени.

Подробнее на операции дифференцирования мы остановимся позже. Пока лишь добавим, что функция X ( t ) по отношению к функции V ( t ) называется «первообразной функции V ( t ) ». Обратная операция (нахождение функции, которая после дифференцирования становится производной) называется нахождение первообразной или интегрирование.

Чем замечательна «производная», мы показали. А чем замечательна «первообразная»?

Первообразная функции позволяет найти саму функцию с точностью до некоторой постоянной величины. Таким образом, зная вид производной функции, мы знаем вид самой функции, но с некоторой неопределенностью на постоянную величину.

Мы можем найти функцию координаты X ( t ) = Первообразная ( V ( t )) + const . (где const – обозначение в формулах некоторой постоянной величины) Обычно операцию интегрирования функции записывают с помощью знака интеграла. Он похож на английскую букву S от слова «СУММА».

Таким образом, функция скорости V ( t ) есть производная функции координаты X ( t ) по времени и одновременно первообразной функции ускорения a ( t ) по времени.

Функция ускорения a ( t ) есть производная функции скорости V ( t ) по времени. И одновременно второй производной функции координаты X ( t ) по времени. И т.д.

Надеюсь, теперь у вас сформировалось начальное понимание, что такое «скорость» и «ускорение» в точном физическом смысле. В смысле, удобном для решения задач на движение тел.

Собственно, это все, что нужно знать про механическое движение для успешного решения задач школьной (и любой другой) Механики!

И в заключение. Самое важное в данном параграфе, следующее:

Рассмотрим функцию зависимости координаты тела (материальной точки) от времениX(t).

Зная ее, мы знаем положение тела в каждый момент времени t.

Оказывается, существует простой способ получения из этой функции X(t) другой функцииV(t), которая является функцией зависимости мгновенной скорости тела от времени.

Операция получения функции скорости из функции координаты называется «Дифференцирование». А функция, полученная путем такой операции, называется «Производная» первоначальной функции.

Таким образом говорят, что скорость есть первая производная пути.

Подробнее это будет рассмотрено ниже.

. И еще одно важное замечание. До сих пор шла речь о скорости механического движения. Но все наши рассуждения полностью справедливы для скорости изменения любой другой физической величины. Если известна функция зависимости одной физической величины от другой физической величины, называемой «переменной» (от любой другой, а не только от времени), то производная функции по этой переменной есть функция скорости изменения физической величины в зависимости от изменения нашей переменной.

Забегая вперед приведем пример: Представим, что для каждой точки пространства определена температура вещества в этой точке. И нам известна функция распределения температуры в зависимости от изменения координаты точки. Тогда мы можем вычислить функцию зависимости скорости изменения температуры при пространственном сдвиге по координате (так называемого «пространственного градиента температуры»). Она есть производная нашей функции зависимости температуры от координаты по этой координате.

Источник