Минимальная длина кодовых слов потому что получился двоичный
5. Кодирование и декодирование
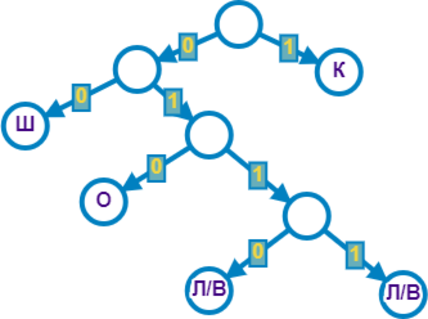
Для кодирования последовательности, состоящей из букв слова ШKOЛKOВО решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Ш использовали кодовое слово 00, для буквы К — 1. Укажите, какова наименьшая длина всех символов заданного слова.
Построим дерево для решения задачи. Для букв Ш и К есть кодовые слова 00 и 1 соответственно. В слове ШКОЛКОВО самая частовстречаемая буква — О, следовательно, её нужно закодировать минимальновозможным количеством символов.
Минимально возможная длина кодового слова для буквы состоит из трёх битов, то есть О закодируем с помощью 010.
Буквы Л и В встречаются всего один раз, закодируем их минимально возможным количеством символов.
Самая маленькая длина кодовых слов для них \(=4\) : 0110 и 0111.
Посчитаем сумму длин кодовых слов:
Ш, Л и В встречаются один раз,
Для кодирования последовательности, состоящей из букв слова Р, Б, О, Т, А используется неравномерный двоичный код, удовлетворяющий прямому условию Фано.
Вот этот код: А – 0; Р – 100; Б – 1010; О – 111; Т – 110. Необходимо сократить для одной из букв длину кодового слова так, чтобы код можно было однозначно декодировать.
Для какой буквы это возможно сделать? В ответе укажите эту букву.
Так как код удовлетворяет прямому условию Фано (ни одно кодовое слово не является началом другого), то следует учитывать это при сокращении исходных кодовых слов.
1. Код буквы А сократить нельзя, так как он состоит всего из одного символа.
2. Р сократить нельзя,так как при сокращении до 10 код перестанет удовлетворять прямому условию Фано.
3. Б возможно сократить до 101, в таком случае код по-прежнему будет удовлетворять одному из условий Фано (прямому).
4. О нельзя сократить, т.к. в этом случае нарушится прямое условие Фано.
5. Код буквы Т нельзя сократить, т.к тогда он совпадёт с началом кода буквы О, что недопустимо при выполнении прямого условия Фано.
По каналу связи передаются сообщения, которые содержат только следующие буквы: С, Т, Р, И, М; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв С, Т, Р используются такие кодовые слова: С – 0; Т – 110; Р – 101. Укажите кратчайшее кодовое слово для буквы И, при котором код будет допускать однозначную расшифровку. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Построим дерево решений. Код не может начинаться с нуля, т.к из данной вершины нельзя построить новые варианты, удовлетворяющие условию Фано. Из схемы видно, что для букв И, М есть два возможных варианта кодировки,которые начинаются с 1.
Первый вариант: 111
Второй вариант: 100
Оба варианта удовлетворяют условию Фано (не являются началом других кодовых слов), нам подходит вариант с наименьшим значением, то есть 100 — ответ.
Минимальная длина кодовых слов потому что получился двоичный
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали кодовые слова 100, 101, 00, 01 соответственно. Для двух оставшихся букв — Д и Е — коды неизвестны.
Укажите кратчайшее кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Для четырёх букв кодовые слова уже известны, осталось подобрать для буквы Д такое кодовое слово, которое будет являться кратчайшим и удовлетворять условию Фано.
Кодовым словом не могут быть ни 0, ни 1, потому что есть кодовые слова, начинающиеся с 0 и 1. Для оставшейся буквы можно использовать кодовые слова 110 и 111. Кратчайшее слово с наименьшим числовым значением — 110.
Для кодирования некоторой последовательности, состоящей только из букв А, Б, В, Г, Д, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В использовали соответственно кодовые слова 1, 00, 0100. Укажите минимальную возможную суммарную длину для букв Г и Д, если известно, что код должен допускать однозначное декодирование.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Для трёх букв кодовые слова уже известны, осталось подобрать для букв Г и Д такие кодовые слова, которые будут являться кратчайшим и удовлетворять условию Фано.
Кодовым словом не могут быть ни 0, ни 1, потому что есть кодовые слова, начинающиеся с 0 и 1. Для оставшихся букв можно использовать кодовые слова 011 и 0101. Сумма длин этих кодовых слов равна 7.
Для кодирования некоторой последовательности, состоящей только из букв А, Б, В, Г, Д, Е решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б использовали соответственно кодовые слова 00, 01. Какова наименьшая возможная сумма длин кодовых букв В, Г, Д, Е, при котором код будет допускать однозначное декодирование.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Кодовые слова для букв В, Г, Д и Е не могут начинаться с 0, поскольку кодовые слова для букв А и Б это 00 и 01. Значит, кодовыми словами для букв В, Г, Д и Е будут 100, 101, 110 и 111. Сумма длин кодовых слов для букв В, Г, Д и Е равна 12.
По каналу связи передаются сообщения, содержащие только 4 буквы:
В любом сообщении больше всего букв О, следующая по частоте буква − Е, затем − Н. Буква Т встречается реже, чем любая другая.
Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать?
3) Е−1, Н−01, O−001, Т−000
4) О−0, Н−11, Е−101, Т−100
Выберем коды, для которых выполнено условие Фано. Это коды 3 и 4.
Чтобы сообщение было как можно короче, необходимо, чтобы чем чаще встречалась буква, тем короче был ее код.
Следовательно, ответ 4, поскольку буква О — самая часто встречающаяся буква и для ее кодирования в варианте 4 используется один символ.
По каналу связи передаются сообщения, содержащие только 4 буквы:
В любом сообщении больше всего букв А, следующая по частоте буква — С, затем — И. Буква Т встречается реже, чем любая другая.
Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать?
3) А−1, И−01, С−001, Т−000
4) С−0, И−11, А−101, Т−100
Выберем коды, для которых выполнено условие Фано. Это коды 3 и 4. Чтобы сообщение было как можно короче, необходимо, чтобы чем чаще встречалась буква, тем короче был ее код.
Следовательно, ответ 3, поскольку буква А — самая часто встречающаяся буква и для ее кодирования в варианте 3 используется один символ.
По каналу связи передаются сообщения, каждое из которых содержит 16 букв А, 8 букв Б, 4 буквы В и 4 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования:
а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);
б) общая длина закодированного сообщения должна быть как можно меньше.
Какой код из приведённых ниже следует выбрать для кодирования букв А, Б, В и Г?
1) А:0, Б:10, В:110, Г:111
3) А:1, Б:01, В:011, Г:001
2 и 3 не подходят, так как в них встречаются пары кодов, один из которых является началом другого.
Длина сообщений при использовании первого кода будет равна .
Длина сообщений при использовании четвёртого кода будет равна .
При использовании первого кода сообщения получаются короче, поэтому следует использовать именно его.
По каналу связи передаются сообщения, содержащие только буквы А, Б, В, Г, Д, Е. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано; для букв A, Б, В используются такие кодовые слова: А — 0, Б — 101, В — 110.
Какова наименьшая возможная суммарная длина всех кодовых слов? Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
Рассмотрели все коды с длинами от 1 до 3, поэтому теперь достаточно взять любые два подходящие кода длины 4. Например, 1000 и 1001.
В сумме длина кодов 1 + 3 + 3 + 3 + 4 + 4 = 18.
По каналу связи передаются сообщения, содержащие только буквы А, Б, В, Г, Д, Е. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано; для букв A, Б, В используются такие кодовые слова: А — 1, Б – 010, В – 001.
Какова наименьшая возможная суммарная длина всех кодовых слов? Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
Рассмотрели все коды с длинами от 1 до 3, поэтому теперь достаточно взять любые два подходящие кода длины 4. Например, 0111 и 0110.
В сумме длина кодов 1 + 3 + 3 + 3 + 4 + 4 = 18.
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А – 11, B – 101, C – 0. Какова наименьшая возможная суммарная длина всех кодовых слов?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
Заметим, что для алфавита из трёх букв, код с наименьшей суммарной длиной кодовых слов, удовлетворяющий условию Фано имел бы длину 1 + 2 + 2 = 5. Для алфавита из четырёх букв: 1 + 2 + 3 + 3 = 9. Аналогично можно получить минимальную длину суммарную длину кодовых слов для алфавита, содержащего произвольное число символов.
Удостоверимся, что, используя кодовые слова, приведённые в условии можно построить код, удовлетворяющий условию Фано и имеющий наименьшую суммарную длину. Будем использовать для буквы D кодовое слово 1000, для буквы E кодовое слово 10010, для буквы F 10011.
Суммарная длина такого кода 1 + 2 + 3 + 4 + 5 + 5 = 20.
Конспект урока по информатике: «Дискретное кодирование» (8 класс)
Выберите документ из архива для просмотра:
Выбранный для просмотра документ 3. Дискретное кодирование 8 кл..ppt
Описание презентации по отдельным слайдам:
Описание слайда:
Кодирование информации
§ 5. Дискретное кодирование
1
Описание слайда:
Дискретизация
2
Дискретизация — это представление единого объекта в виде множества отдельных элементов.
t = 18°C
20
40
0
60
80
100
120
км/ч
км/ч
110
110,231 км/ч?
?
Описание слайда:
Хранение данных в компьютере
3
0
0
0
0
1
1
Компьютер — это дискретное устройство.
Двоичный код – это код, в котором используются два знака (0 и 1). Все данные в компьютере хранятся в двоичном коде.
Бит – это одна двоичная цифра (0 или 1).
010010
Сколько бит?
?
Описание слайда:
Двоичное кодирование
4
Кодовая таблица
кодовое слово
ГАГАРА:
010 000 010 000 100 000
Равномерный код — это код, в котором все кодовые слова имеют одинаковую длину.
Сколько существует кодовых слов длиной N
в двоичном коде?
?
2N
Описание слайда:
Декодирование
5
Кодовая таблица
Р А Г Р А
100000010100000
?:
Декодирование — это восстановление исходного сообщения из кода.
Сколько символов было в сообщении?
?
5
100 000 010 100 000
Как разбить на кодовые слова?
?
по 3
Описание слайда:
Описание слайда:
Неравномерные коды
7
Недостаток равномерных кодов – длинные закодированные сообщения.
Идея: часто встречающиеся символы должны иметь более короткие коды!
Описание слайда:
Неравномерные коды
8
Кодовая таблица
ГАГАРА:
1 0 1 0 10 0
Неравномерный код — это код, в котором кодовые слова имеют разную длину.
Декодирование: 010010
Не всегда
однозначно!
!
АРАР
АГААР
АPАГА
АГААГА
Как выделить
кодовые слова?
?
Описание слайда:
Неравномерные коды
9
Кодовая таблица
Декодирование: 01001011
АГАГР
Неравномерный код декодируется однозначно, если выполняется условие Фано: ни одно кодовое слово не совпадает с началом
другого кодового слова.
Описание слайда:
Описание слайда:
Как измерить информацию?
11
10101001010
данные (код)
Количество информации в битах определяется длиной сообщения в двоичном коде.
10101100
8 битов
Описание слайда:
Единицы измерения
12
1 байт = 8 бит
1 Кбайт (килобайт) = 1024 байта
1 Мбайт (мегабайт) = 1024 Кбайт
1 Гбайт (гигабайт) = 1024 Мбайт
1 Тбайт (терабайт) = 1024 Гбайт
210
1 байт = 23 бит
1 Кбайт = 210 байта = 210 23 бит = 213 бит
1 Мбайт = 210 Кбайт = 210 213 бит = 223 бит
Описание слайда:
Перевод в другие единицы
13
2 Кбайт = 2 (1 Кбайт) = 2 1024 байт
= 2048 байт
= 2048 (1 байт) = 2048 8 бит
= 16 384 бита
Через степени числа 2:
2 Кбайт = 2 210 байт = 211 байт
= 211 23 бит = 214 бит.
Описание слайда:
Перевод в другие единицы
14
1 байт
1 бит
1 Кбайт
1 Мбайт
1 Гбайт
1 Тбайт
: 8
: 1024
: 1024
: 1024
: 1024
1024
1024
1024
1024
8
1 байт = 8 бит
1 Кбайт = 1024 байта
число уменьшается
число увеличивается
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Выводы:
20
Дискретизация – это представление единого объекта в виде множества отдельных элементов.
Компьютеры обрабатывают информацию в двоичном коде, в котором используется два знака (обычно 0 и 1).
Данные, с которыми работает компьютер – дискретные. Для того чтобы информацию можно было обрабатывать с помощью компьютеров, её нужно дискретизировать – перевести в дискретный вид. Как правило, дискретизация приводит к потере части информации.
Равномерный код – это код, в котором все кодовые слова имеют одинаковую длину.
Неравномерный код – это код, в котором кодовые слова имеют различную длину.
Декодирование – это восстановление исходного сообщения из кода.
Сообщения, закодированные с помощью неравномерного кода, не всегда можно декодировать однозначно.
Неравномерный код декодируется однозначно, если выполняется условие Фано: ни одно кодовое слово не совпадает с началом другого кодового слова.
С помощью i битов можно закодировать 2i различных вариантов.
Описание слайда:
Описание слайда:
22
Задание на дом:
§ 5, стр. 33-41, (образцы заданий на сайте Решу ОГЭ, сайт К.Ю. Полякова)
Выводы, стр. 39-40 учебника.
Подводя итог урока, я бы хотел узнать:
— что нового вы сегодня узнали
— какие моменты урока вам особенно запомнились
Итоги урока:
Описание слайда:
Источники иллюстраций
23
http://fpg.unc.edu
http://s1.iconbird.com
https://sandstorm.deviantart.com
http://compression.ru
http://ru.wikipedia.org
https://www.kns.ru
http://nix.ru
http://www.computer-services.ru
http://www.masterna4as.com
http://blendercontest.com
http://geeky-gadgets.com
авторские материалы
Выбранный для просмотра документ Урок 3. Дискретное кодирование 8 кл.docx
Урок 3. Дискретное кодирование §5. (8 класс)
Нужно объяснить учащимся, что компьютеры — это дискретные устройства, поэтому для ввода любой информации в компьютер нужно перевести её в дискретный вид, то есть выполнить дискретизацию.
Учащиеся должны освоить равномерное и неравномерное кодирование и декодирование по заданной кодовой таблице. Они должны понять, что неравномерное кодирование не всегда позволяет однозначно декодировать сообщение.
Для компьютеров, которые не понимают смысла сообщений, важна только длина полученного при кодировании двоичного кода, которая определяет время обработки и передачи данных. Длина двоичной последовательности называется количеством информации.
В конце урока выполняется тест № 4. При нехватке времени он может быть задан в качестве домашнего задания. Онлайн- варианты всех тестов находятся по адресу
Задачи: систематизировать знания и умения учащихся
развивать коммуникативные навыки общения и умения говорить, слушать и слышать
воспитывать аккуратность, дисциплину, ответственное отношение к учёбе,
самостоятельность, бережное отношение к школьному имуществу.
Тип урока: изучение нового материала
Оборудование: учебник, тетрадь, презентация, интерактивная панель.
Тест3. Язык и кодирование
Объяснение нового материала.
В чём принципиальное различие между картиной, нарисованной красками, и мозаикой?
Информация, существовавшая ранее у нас в сознании в виде мыслей, записывается в виде отдельных «кусочков», знаков. Такая процедура называется дискретизацией.
Дискретизация — это представление непрерывного объекта в виде множества отдельных элементов.
Может ли цифровой спидометр показать скорость 110,231 км/ч? Почему?
Как вы знаете, все виды информации в компьютере представлены в двоичном коде, как цепочки нулей и единиц. Это не случайно, потому что для хранения каждого бита в компьютере используется электронный блок с двумя состояниями. Поэтому компьютер — это дискретное устройство.
Для того чтобы ввести данные в компьютер, нужно выполнить их дискретизацию, например, представить текст как набор букв, а рисунок — как набор пикселей. Затем каждому элементу (букве, пикселю) нужно присвоить двоичный код — битовую цепочку.
2. Равномерные коды
Если нам нужно записать в память компьютера какой-то текст на русском языке, его нужно представить в виде двоичного кода, т. е. перекодировать.
Например, перекодируем слово ГАГАРА в двоичный алфавит, считая, что в тексте есть только буквы «А», «Г» и «Р», т. е. алфавит состоит из трёх знаков. Присвоим каждой из этих букв двоичные коды — кодовые слова (рис. 2.5).
Закодируйте с помощью этого кода слово ГАГАРА.
Такой код называется равномерным, потому что длина всех кодовых слов одинакова.
Равномерный код — это код, в котором все кодовые слова имеют одинаковую длину.
Теперь предположим, что по компьютерной сети передана цепочка
Известно, что для кодирования использовалась таблица, показанная на рис. 2.5, и нам нужно узнать, какое сообщение было закодировано. Эта операция называется декодированием.
Декодирование — это восстановление исходного сообщения из кода.
Длину кодовых слов L выбирают из условия M L ≥ M0, где М0 — мощность алфавита исходного сообщения и М — мощность нового алфавита.
Как выбрать наименьшую возможную длину кодовых слов при равномерном кодировании?
3. Неравномерные коды
Недостаток равномерного кода в том, что закодированные сообщения получаются довольно длинными, и на их передачу компьютерная система тратит много времени. Попробуем сократить длину сообщения, используя кодовые слова разной длины, например, так (рис. 2.6).
Рис. 2.6
Такой код называется неравномерным.
Закодируйте с помощью этого кода слово ГАГАРА.
При использовании равномерного или неравномерного кода закодированное сообщение получилось короче?
Декодируйте сообщение 010010, закодированное с помощью кода на рис. 2.6. Попробуйте построить разные варианты декодированного сообщения.
Вывод: Сообщения, закодированные с помощью неравномерного кода, не всегда можно декодировать однозначно .
Есть ли такие неравномерные коды, сообщения в которых однозначно декодируются? Оказывается, есть. Например, такой код (рис. 2.7).
Рис. 2.7
Закодируйте с помощью этого кода слово ГАГАРА. Сравните длины полученного закодированного сообщения и сообщений, которые вы построили ранее.
Какое из них самое короткое? Самое длинное?
Декодируйте сообщение 01001011, закодированное с помощью кода на рис. 2.7. Попробуйте построить различные варианты декодирования.
Неравномерный код декодируется однозначно, если выполняется
условие Фано: ни одно кодовое слово не совпадает с началом другого кодового слова .
Долгое время для передачи сообщений по телеграфу и радио применялся код Морзе (азбука Морзе), предложенный американским художником и изобретателем Самюэлем Морзе. В этом коде все буквы и цифры кодируются в виде различных последовательностей точек и тире. (таблица кодов стр. 38)
Определите, к каким кодам относится код Морзе — к равномерным или неравномерным. Как вы рассуждали?
Как вы думаете, какие буквы должны иметь более короткие коды: те, которые в текстах встречаются чаще, или те, которые встречаются реже?
5. Измерение количества информации
Давайте вспомним, как измеряется количество информации (данных) в компьютерных системах. Сообщение кодируется с помощью двоичного кода, и количество информации в битах определяется как длина полученной битовой цепочки.
Сколько бит информации содержится в сообщении 10100011?
Сколько знаков содержит алфавит двоичного кода?
Определите, сколько различных сообщений можно закодировать с помощью i бит.
На практике используются следующие единицы количества информации:
1 Кбайт = 1024 байта = 2 10 байта = 2 13 бит.
1 Мбайт = 1024 Кбайт = 2 20 байта = 2 23 бит.
1 Гбайт = 1024 Мбайт.
1 Тбайт = 1024 Гбайт.
6. Алфавитный подход (решение задач)
Закрепление полученных знаний. Формирование умений и навыков
Ответить на вопросы к параграфу
Составить интеллект-карту (если останется время)
Выводы, стр. 39-40 учебника. Рефлексия
§ 5, стр. 33-41, по желанию подготовить сообщение по темам указанным на стр. 41.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Минимальная длина кодовых слов потому что получился двоичный
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 000, Б — 01, В — 1101, Г — 111, Д — 0010, Е — 100. Для кодирования слова ГОРОД потребовалось 17 двоичных знаков. Какое кодовое слово соответствует букве О?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Кодовые слова для букв Г и Д уже известны, для кодирования этих двух букв потребуется 7 двоичных знаков. Поскольку буква О повторяется в слове ГОРОД два раза, закодируем её кодовым словом 101. Букву Р закодируем кодовым словом длины 4. Всего для кодирования слова ГОРОД в таком случае потребуется 17 двоичных знаков. Таким образом, ответ — 101.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: В — 0100, Г — 0111, Д — 11, Р — 1011. Для кодирования слова АНАГРАММА потребовалось 26 двоичных знаков. Какое кодовое слово соответствует букве М?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Буква А повторяется в слове АНАГРАММА 4 раза. Закодируем её кодовым словом 00. Тогда буквы А, Г, Р занимают в слове 16 двоичных знаков. На две буквы М и одну Н приходится 26 − 16 = 10 двоичных символов. Букву М закодировать кодовым словом длины 4 нельзя, поскольку не останется таких кодовых слов для буквы Н, чтобы соответствовать условию. Значит, букву М закодируем кодовым словом 100. Тогда ответ — 100.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 101, В — 1001, Г — 111, Д — 0110, Е — 110. Для кодирования слова ОГОРОД потребовалось 17 двоичных знаков. Какое кодовое слово соответствует букве О?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Кодовые слова для букв Г и Д уже известны, для кодирования этих двух букв потребуется 7 двоичных знаков. Поскольку буква О повторяется в слове ОГОРОД три раза, закодируем её кодовым словом 00. Букву Р закодируем кодовым словом длины 4. Всего для кодирования слова ОГОРОД в таком случае потребуется 17 двоичных знаков. Таким образом, ответ — 00.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: В — 01, Г — 1001, Д — 0001, Т — 0010. Для кодирования слова ИНФИНИТИВ потребовалось 24 двоичных знака. Какое кодовое слово соответствует букве Н?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Буква И повторяется в слове ИНФИНИТИВ 4 раза. Закодируем её кодовым словом 11. Тогда буквы В, Н, Т и Ф занимают в слове 16 двоичных знаков. На две буквы Н и одну Ф приходится 24 − 8 − 4 − 2 = 10 двоичных символов. Букву Ф закодировать кодовым словом длины 3 нельзя, поскольку не останется таких кодовых слов для буквы Н, чтобы соответствовать условию. Значит, букву Ф закодируем кодовым словом 1000. Тогда ответ — 101.
Для кодирования некоторой последовательности используют следующую кодировочную таблицу: