Мко что это такое
Мко что это такое
Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.
Межамериканский комитет обороны
Словарь: Словарь сокращений и аббревиатур армии и спецслужб. Сост. А. А. Щелоков. — М.: ООО «Издательство АСТ», ЗАО «Издательский дом Гелеос», 2003. — 318 с.
Международная комиссия по освещению
Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.
Московское купеческое общество
метод конечных объёмов
муниципальная краткосрочная облигация
Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.
Словарь: Словарь сокращений и аббревиатур армии и спецслужб. Сост. А. А. Щелоков. — М.: ООО «Издательство АСТ», ЗАО «Издательский дом Гелеос», 2003. — 318 с.
Международный культурный обмен
центр «Медицинское корпоративное обслуживание»
Московский комитет образования
Москва, образование и наука
Международная комиссия по озону
механическая кулинарная обработка
международная коммерческая операция
масло кедрового ореха
Международная космическая олимпиада
косм., образование и наука, спорт
мультиплексный канал обмена
Полезное
Смотреть что такое «МКО» в других словарях:
МКО (x, y, Y) — (МКО (X, Y, Z), МКО (1931)) модель цветового пространства, рекомендованная МКО для вычисления координат цвета. Разработана в 1931 г. на основании экспериментальных данных для малого угла зрения 20° (для стандартного наблюдателя 20°). За основу… … Реклама и полиграфия
МКО — Международная комиссия по освещению см.: CIE … Реклама и полиграфия
МКО (Λd, PE, Y) — альтернативный способ обозначения цвета. Цветность характеризуется доминирующей длиной волны (λD) и условной чистотой цвета (Pe), а координата Y характеризует яркость (коэффициент яркости) … Реклама и полиграфия
ємко — Присл. до ємкий … Український тлумачний словник
ёмко — см. ёмкий; нареч … Словарь многих выражений
МКО — машинно котельное отделение мебельно коммерческое объединение Межамериканский комитет обороны Международная комиссия по озону Международная комиссия по освещению Международный культурный обмен муниципальная краткосрочная облигация … Словарь сокращений русского языка
МКО (x10, y10, Y10) — (МКО (X10, Y10, Z10), МКО (1964)) модель, аналогичная МКО (1931), но для большего угла зрения, который равен 10°, т. е. для стандартного наблюдателя 10°. Модель разработана в 1964 г … Реклама и полиграфия
Мко что это такое
Российский национальный комитет Международной комиссии по освещению
Международная комиссия по освещению (МКО) — старейшая международная организация по вопросам света и освещения, основанная в 1913 г. МКО является высшим авторитетом по вопросам освещения, признанным Международной организацией по стандартизации (ISO) и Международной электротехнической комиссией (IEC) как международный орган по стандартизации в области освещения.
Цели Международной комиссии по освещению
О Российском национальном комитете МКО
Российские светотехники участвуют в МКО с 1935 года. На протяжение более чем 80 лет Россия представлена в этой международной организации, и даже в самые непростые для нашей страны времена у российских учёных была возможность принимать активное участие в технических комитетах МКО, получать самые современные стандарты и технические руководства Комиссии. С 1959 г. базовой организацией Российского национального комитета является ВНИСИ.
Состав Российского национального комитета МКО
Президент РНК МКО, Вице-президент МКО
А.Г. Шахпарунянц, Генеральный директор ВНИСИ
Глава Отделения 1 РНК (Зрение и свет)
В.Ю. Снетков, к.т.н., доцент, НИУ «МЭИ»
Глава Отделения 2 РНК (Фотометрия и радиометрия)
Р.И. Столяревская, д.т.н., ВНИСИ
Глава Отделения 3 РНК (Внутреннее освещение и световой дизайн)
Ю.Б. Айзенберг, д.т.н., профессор, шеф-редактор журнала «Светотехника / Light & Engineering»
Глава Отделения 4 РНК (Наружное освещение и освещение на транспорте)
А.А. Коробко, к.т.н., МСК «БЛ Групп»
Глава Отделения 6 РНК (Фотобиология и фотохимия)
Р.И. Беляев, главный метролог ВНИСИ
Глава Отделения 8 РНК (Технология изображения и визуализация)
В.П. Будак, д.т.н., профессор, главный редактор журнала «Светотехника / Light & Engineering»
Публикации МКО
Стандарты и технические рекомендации МКО являются всемирно признанными руководящими документами по применению света и освещения. Над их созданием работают Международные технические комитеты, объединённые в Отделения МКО.
У членов Национального комитета есть уникальная возможность приобретения итоговых публикаций МКО по специальной цене.
Контактная информация
Секретарь Российского национального комитета МКО — Павел Федорищев, руководитель группы по международному сотрудничеству ВНИСИ
Мко что это такое
Москва, образование и наука
Международная комиссия по освещению
мобильный комплекс оборудования для поиска, обнаружения и обследования подводных потенциально опасных объектов
мобильный комплекс оборудования химического контроля акваторий
мобильный комплекс оборудования радиационного контроля акваторий
Центральное окружное управление Московского комитета образования
Москва, образование и наука
Юго-Западное окружное управление образованием Московского комитета образования
Москва, образование и наука
«Региональная медико-фармацевтическая научно-образовательная конференция» «Региональная медико-фармацевтическая научно-образовательная конференция и профессиональный конкурс»
мед., образование и наука
Международная конфедерация обществ потребителей
заместитель комиссара по морским делам
Вакцина против коронавирусной инфекции разработки НИЦЭМ имени Гамалеи
максимально корригированная острота зрения
заместитель командующего по морским делам
заместитель командующего корпусом
служба финансового мониторинга и корреспондентских отношений
домовой комитет бедноты
из архивных источников за 1920 год
Институт мониторинга качества образования
образование и наука, организация, Украина
межрегиональная кинологическая общественная организация
Иван Марангозов копирует оригинал
Северо-западное межрегиональное коммерческое объединение
муниципальное казённое общеобразовательное учреждение
Войнович В.: Москва 2042 / Владимир Войнович. – М.:Эксмо, 2009. – 384 с., с.151
Общемосковский классификатор органов исполнительной власти города Москвы
функциональный канал мультиплексированного обмена
множественный поток команд, одиночный поток данных
Камский коммерческий банк
г. Набережные Челны
Криворожский горно-металлургический комбинат окисленных руд
Кировоградская обл., организация, Украина
отдел технологии коммерческой работы департамента грузовой и коммерческой работы
Балтийский и международный морской совет Балтийская и международная морская конференция
Международная комиссия по морским млекопитающим северной части Атлантического океана
Всесоюзная хозрасчётная контора по выращиванию посадочного материала и заготовке древесно-кустарниковых семян
Министерства земледелия СССР
Центральная контора по заготовке, переработке и сбыту древесины, плодовых и кустарниковых пород
Главного управления по лесонасаждению Наркомзёма СССР
г. Рим, Санкт-Петербург
государственный земельный контроль
метод комплексной оценки товарной системы
центр менеджмента качества в образовании
образование и наука
комплекс методов квалификационной оценки
Республиканский центр мониторинга качества образования
ГУ РЦМКО при МОиН РТ
образование и наука
комиссия по контактам
А. и Б. Стругацкие, «Жук в муравейнике»
Ассоциация музеев космонавтики
косм., муз., организация
начальник Главного управления организации таможенного контроля
Федеральная служба по надзору за соблюдением законодательства в сфере массовых коммуникаций и охране культурного наследия
Международный кодекс по охране судов и портовых средств
комитет по фармацевтической деятельности
электромагнитный клапан открытия
комиссия по проведению режима экономии
г. Екатеринбург, организация, фин.
уездный земельный комитет
Аверченко. А. Дюжина ножей в спину революции. — Предисловие // http://text.marsu.ru/RUSSLIT/AWERCHENKO/predisl.html
Трест конструкторских работ Главпромстроя Министерства транспортного строительства СССР
Главное управление по комплектованию предприятий химической, целлюлозно-бумажной и химико-фармацевтической промышленности при Госснабе СССР
мед., организация, СССР, хим.
сельский земельный комитет
Главное управление по комплектной поставке оборудования для строящихся и реконструируемых предприятий химической промышленности при Совете народного хозяйства РСФСР
районный промышленный комбинат
председатель земельного комитета
помощник командира роты
помощник командира дивизиона
помощник командира дивизии
помощник командира взвода
помощник командира бригады
помощник командира батальона
Национальная инвестиционная металлургическая компания
Народный комиссариат коммунального хозяйства
Международная комиссия по окружающей среде и развитию
ЗАО «Московская телекоммуникационная корпорация»
Комиссия по контролю
Комиссия по контактам с иными цивилизациями
МАШИННО-КОТЕЛЬНОЕ ОТДЕЛЕНИЕ
— помещение на судне, в котором размещены главные двигатели (судовая машина) и котлы.
Смотреть что такое «МАШИННО-КОТЕЛЬНОЕ ОТДЕЛЕНИЕ» в других словарях:
КОТЕЛЬНОЕ ОТДЕЛЕНИЕ — (Boiler compartment, boiler room) специальное помещение на судне, в котором установлены котлы. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 Котельное отделение помещение на кор … Морской словарь
Котельное отделение — (англ. boiler compartment, boiler room) специальное помещение на судне или корабле, в котором устанавливаются паровые котлы главной энергетической установки, а также оборудование и устройства, необходимые для собственной работы котлов … Википедия
МАШИННОЕ ОТДЕЛЕНИЕ МО — судовое помещение или группа помещений, в которых установлены главные и вспомогательные энергетические установки. В Машинном Отделении размещают также механическую мастерскую, насосы балластной и других общесудовых систем и посты местного или… … Морской энциклопедический справочник
МКО — машинно котельное отделение мебельно коммерческое объединение Межамериканский комитет обороны Международная комиссия по озону Международная комиссия по освещению Международный культурный обмен муниципальная краткосрочная облигация … Словарь сокращений русского языка
Крейсер «Аврора» — «Аврора» Современный вид крейсера «Аврора» ночью Основная информация Тип Крейсер I ранга … Википедия
Крейсер «Аврора» — «Аврора» Современный вид крейсера «Аврора» ночью Основная информация Тип Крейсер I ранга … Википедия
Крейсер Аврора — «Аврора» Современный вид крейсера «Аврора» ночью Основная информация Тип Крейсер I ранга … Википедия
Эскадренные миноносцы проекта 56 — (тип «Спокойный») … Википедия
Аврора (крейсер) — У этого термина существуют и другие значения, см. Аврора (значения). «Аврора» … Википедия
МКЭ или МКО
Среди инженеров-расчётчиков, моделирующих течения жидкости и газа, уже давно идёт спор о том, насколько метод конечных элементов (МКЭ) подходит для решения задач вычислительной гидродинамики (CFD). Есть специалисты, которые твёрдо убеждены в превосходстве метода контрольного объёма (МКО) над методом конечных элементов. Но имеются ли научные основания у этого убеждения? В общем-то, их нет. Разные задачи можно решать разными методами. Давайте узнаем, почему.
Наука, технология и традиция
Метод конечных элементов активно применяется специалистами по численному анализу для моделирования течений жидкости. Опубликовано огромное множество научных работ, посвящённых использованию МКЭ в CFD, в том числе новейших разработок для разрывных методов Галёркина (DG), которые являются разновидностью МКЭ с разрывными базисными функциями.
Исторически так сложилось, что в коммерческих CFD кодах обычно используется метод контрольного объёма. Чаще всего это связано с тем, что в основе всех крупных коммерческих CFD пакетов, как правило, лежит общий программный код. Отрасль вложила огромный объём труда и технологий в этот код. Разработаны различные методы для эффективного и точного расчёта и интегрирования потоков как на структурированных (например, состоящих из шестигранников), так и для неструктурированных (например, состоящих из тетраэдров) сетках.
И всё же не существует никакого теоретического или практического подтверждения гипотезы о преимуществе МКО над МКЭ. Во-первых, разработано множество вариаций метода контрольного объёма и метода конечных элементов, и в некоторых случаях они имеют много общего. Во-вторых, для практического применения программного обеспечения гораздо большее значение имеет реализация метода в расчётном коде. Можно утверждать, что расчётный код X справляется с определённой группой задач лучше, чем код Y. Однако это не связано с тем, что в одном коде используется МКЭ, а в другом — МКО. Давайте попробуем в этом разобраться.
МКЭ и МКО: что эффективнее?
Математические и численные модели
Рассмотрим обобщенную математическую задачу:
дополненную начальными и граничными условиями:
Здесь P — это дифференциальный оператор, u — зависимая переменная, F — источниковый член уравнения, f — функция, задающая начальное условие, B — оператор, а g — функция, описывающая граничное условие. Переменной x обозначен радиус-вектор с координатами (x, y и z).
Приведённое выше уравнение может быть основой математической модели, которая описывает, например, течение жидкости. Это уравнение является математической формулировкой законов сохранения импульса и массы. Как правило, математические модели, построенные на подобных законах сохранения и дополненные адекватными начальными и граничными условиями, ведут себя вполне корректно. Это означает, что поставленная математическая задача имеет единственное решение, которое непрерывно зависит от входных параметров, то есть от источниковых членов, начальных и граничных условий.
Однако даже в этом случае поиск аналитического решения математической модели может оказаться чрезвычайно сложной или даже невыполнимой задачей. В частности, может быть крайне трудно найти решение в виде аналитического выражения, содержащего легко вычислимые операции (сложение, вычитание, умножение, деление). В этом случае на основе математической модели формулируется аппроксимирующая её численная модель. Уравнения численной модели затем можно решить вычислительными методами, реализованными в компьютерной программе.
МКЭ и МКО — это вычислительные методы, в которых используется пространственная дискретизация уравнений математической модели. Для дискретизации по времени обычно используется та или иная схема дискретизации обыкновенных дифференциальных уравнений. Для представленной выше математической модели можно построить следующую численную модель:
в которой начальные и граничные условия примут вид:
где h — это параметр дискретизации, например размер конечного элемента или контрольного объёма расчётной сетки.
Обратите внимание, что структурные компоненты сетки в одном случае называются элементами, а во втором — контрольными объёмами или ячейками.
Точность вычислительных методов характеризуется разными типами погрешностей или ошибок. Погрешность аппроксимации τ показывает, насколько точно численная модель соответствует математической:
Порядок аппроксимации численной модели показывает, как погрешность аппроксимации зависит от параметра дискретизации h. Чем меньше размер элемента или ячейки, тем точнее численная модель должна соответствовать математической модели. Если погрешность аппроксимации снижается при уменьшении h, тогда численная модель является устойчивой.
Погрешность дискретизации e определяется как разность между точным и численным решениями модельных уравнений:
Говорят, что вычислительный метод сходится, если численное решение приближается к точному при уменьшении h:
Порядок дискретизации p показывает, как быстро численное решение сходится к точному при уменьшении h.
Чем выше порядок дискретизации p, тем быстрее решение сходится к точному.
Существует ли какое-то принципиальное отличие в точности метода конечных элементов и метода контрольного объёма? Повышая степень базисных функций, мы, теоретически, можем получить любой порядок дискретизации метода конечных элементов (на практике, тем не менее, имеются другие ограничения). Фактически, метод конечных элементов чаще всего имеет второй или третий порядок дискретизации, а метод контрольного объёма — первый или второй.
В чём сходство и в чём отличия?
Запишем обобщённое уравнение переноса, которое является основой математических моделей гидродинамики:
В этом уравнении u обозначает аддитивную, удельную на единицу объёма физическую величину, например удельный импульс или плотность; соответственно, Γ — это плотность потока этой величины; например, плотность потока импульса, то есть удельный импульс, который переносится через единицу площади контрольной поверхности в единицу времени.
В рамках метода конечных элементов сначала получим интегральную форму уравнения, умножив члены уравнения на пробные функции φ и проинтегрировав полученное выражение по всей расчётной области:
Далее применим теорему Остроградского-Гаусса:
Здесь ∂Ω — это граница домена Ω, а n — вектор нормали к границе домена. После интегрирования по частям получим:
а значит уравнение (11) можно записать в следующем виде:
Мы получили следующее выражение:
Уравнение (14) можно использовать, чтобы преобразовать второе слагаемое в уравнении (10). Эти преобразования позволяют естественным образом учесть заданные граничные условия для плотности потока в интегральном уравнении. В дальнейшем, при реализации численных алгоритмов таким образом можно снять требование дифференцируемости для вектора плотности потока. В итоге получаем уравнение, которое является отправной точкой для метода конечных элементов:
Это выражение называется слабой формой исходного уравнения. Третье слагаемое в левой части уравнения представляет собой интеграл плотности потока Γ для величины u по всей внешней границе расчётной области ∂Ω. Решение слабой формы уравнения отвечает исходной задаче, только если оно получено для большого набора пробных функций φ. Чаще всего в качестве таких функций используются полиномы, однако можно выбрать и другие функции. Особым частным случаем является пробная функция с постоянным значением, например φ = 1. При использовании таких функций уравнение (15) примет вид:
Эта форма уравнения служит отправной точкой для метода контрольного объёма.
Таким образом, пока никакой разницы между методами конечных элементов и контрольного объёма нет. Мы показали, что уравнение метода контрольного объёма (16) — всего лишь частный случай более общей слабой формы (15), которая используется в методе конечных элементов.
Отличие состоит в дискретизации уравнений (15) и (16). В рамках метода конечных элементов выбирается конечное число пробных функций φ = φh и ставится условие, чтобы для всех этих функций выполнялось равенство (15). В рамках метода контрольного объёма выбирается конечное число контрольных объёмов Ω = Ωh и ставится условие, чтобы для всех этих объёмов выполнялось равенство (16). На рис. 1 и 2 показаны возможные варианты дискретных аналогов, полученных с помощью метода конечных элементов и метода контрольных объёмов, соответственно, когда для пространственной дискретизации используется триангуляция.
В наиболее распространённом на практике варианте метода конечных элементов тестовые функции отличаются от нуля только в некоторой окрестности узловых точек (локально заданные функции). В этом случае интегрирование пробной функции по всей расчётной области, фактически, сводится к интегрированию по элементам (например, треугольным) в окрестности узловой точки. На рис. 1, например, выделенный узел домена и элементы в его окрестностях, окрашены серым цветом. Плотность потока на границах описывается третьим слагаемым в левой части уравнения (15). Эту величину необходимо учитывать только при интегрировании по элементам, некоторые грани (в 3D модели) или рёбра (в 2D модели) которых совпадают с внешней границей, поскольку на внутренних границах, разделяющих элементы, потоки взаимно компенсируются за счёт использования непрерывных базисных функций. На рис. 1 выписаны уравнения для внутренних элементов (выделенных белым, серым и зелёным цветами) и для граничных элементов (выделены голубым цветом), некоторые грани (в 3D) или ребра (в 2D) которых совпадают с внешней границей. В уравнении для выделенного узла, лежащего внутри расчётной области (см. рис. 1), ненулевой вклад в интеграл по Ω даст интегрирование только по ближайшим к узлу элементам. Для выделенного узла, лежащего на внешней границе, ненулевой вклад в интеграл по границе ∂Ω даст интегрирование только по двум ближайшим граничным элементам (выделены голубым цветом), тогда как ненулевой вклад в интеграл по области Ω даст интегрирование по трём близлежащим элементам, включая светло-зеленый элемент.
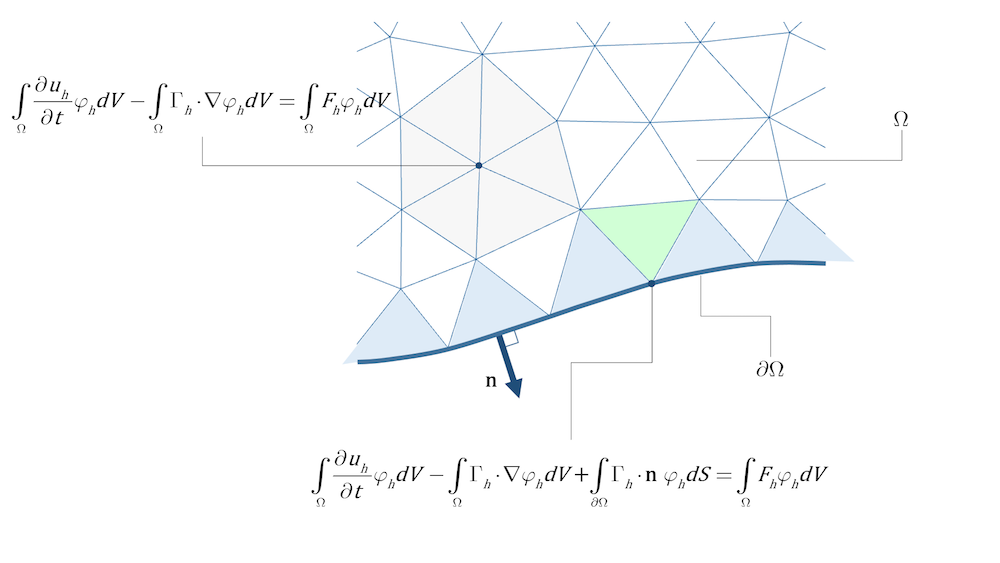
Рисунок 1. Вклад внутренних элементов (отмечены белым и серым цветами) в интеграл по области и вклад граничных элементов в интеграл по границе. В уравнениях для узла, лежащего в центре шестиугольника (закрашенного серым), используются базисные функции, отличные от нуля во всех ближайших элементах, то есть во всех элементах, закрашенных серым. В уравнениях для узла, лежащего на внешней границе области, используются базисные функции, отличные от нуля в ближайших граничных элементах, то есть элементах, у которых грани, рёбра или узлы лежат на внешней границе области (закрашены светло-зелёным и голубым). Ненулевой вклад при интегрировании потока по границе дадут только ближайшие элементы, рёбра которых лежат на внешней границе (закрашены голубым).
Выражение для дискретизации плотности потока внутри расчётной области Γh получим из уравнений сохранения для потока, например, из уравнения конвективной диффузии (в уравнениях гидродинамики диффузионный член описывается законом вязкого трения в уравнении сохранения импульса). Граничные условия, поставленные в конкретной задаче, позволяют получить соотношения для плотности потока на внешней границе в уравнении (15). Это соотношения используются при расчёте интегралов на граничных элементах (на рис. 1 показаны голубым).
Если теперь обратиться к стандартной реализации метода контрольного объёма, то здесь каждая ячейка (треугольник) рассматривается как отдельная область. Второе слагаемое в левой части уравнения (16), содержащее интеграл плотности потока по границе, вычисляется для всех ячеек — как для внутренних, так и для граничных. Плотность потока на гранях или ребрах контрольных объёмов рассчитывается на основе уравнений сохранения, а граничные условия используются для определения плотности потока на гранях и рёбрах, лежащих на внешней границе области (см. рис. 2).
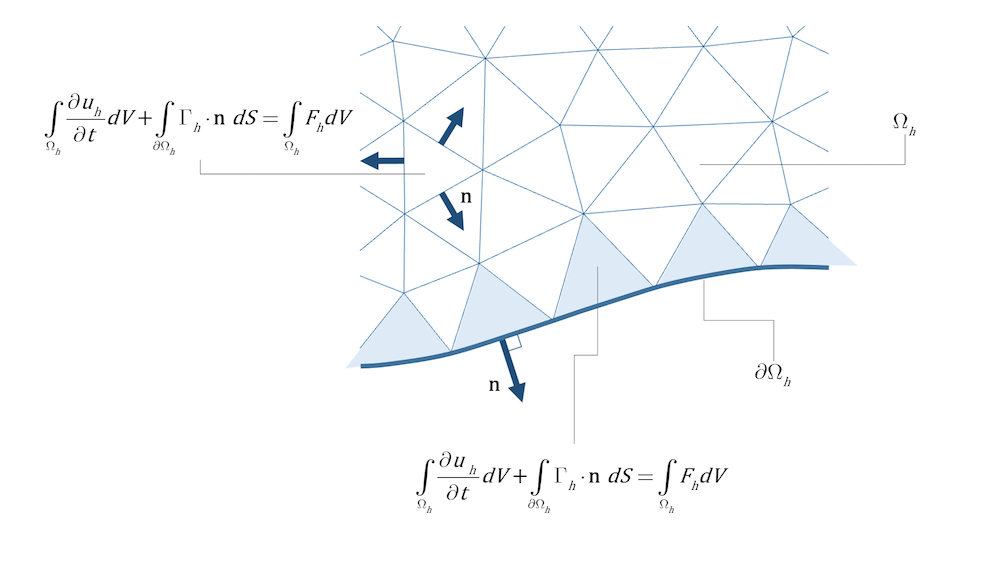
Рисунок 2. Интеграл плотности потока рассчитывают по всем граням (в 3D) или рёбрам (в 2D) контрольных объёмов, как внутренних, так и граничных.
Как получить соотношения для u и Γ этими двумя различными методами?
В МКЭ в качестве базисных функций, аппроксимирующих решение, часто используются пробные функции. Если для аппроксимации решения используются полиномы ненулевого порядка, что позволяет вычислять первые производные, для расчёта плотности конвективного и диффузионного потоков дополнительные соотношения не требуются. Вектор плотности потока в этом случае также описывается локальной полиномиальной функцией.
Напротив, при дискретизации уравнений методом контрольного объёма поток на гранях контрольных объёмов не определён. В МКО решение обычно определено только в центре каждого контрольного объёма. Таким образом, для полноты МКО необходимо дополнить методом реконструкции потока. Как правило, для расчёта производных используют метод локальной интерполяции по соседним ячейкам (см. рис. 3). Чтобы повысить порядок соотношений для интерполяции решения и плотности потока, необходимо использовать значения в большем числе контрольных объёмов. Это усложняет процедуру решения и делает данный метод менее локальным.
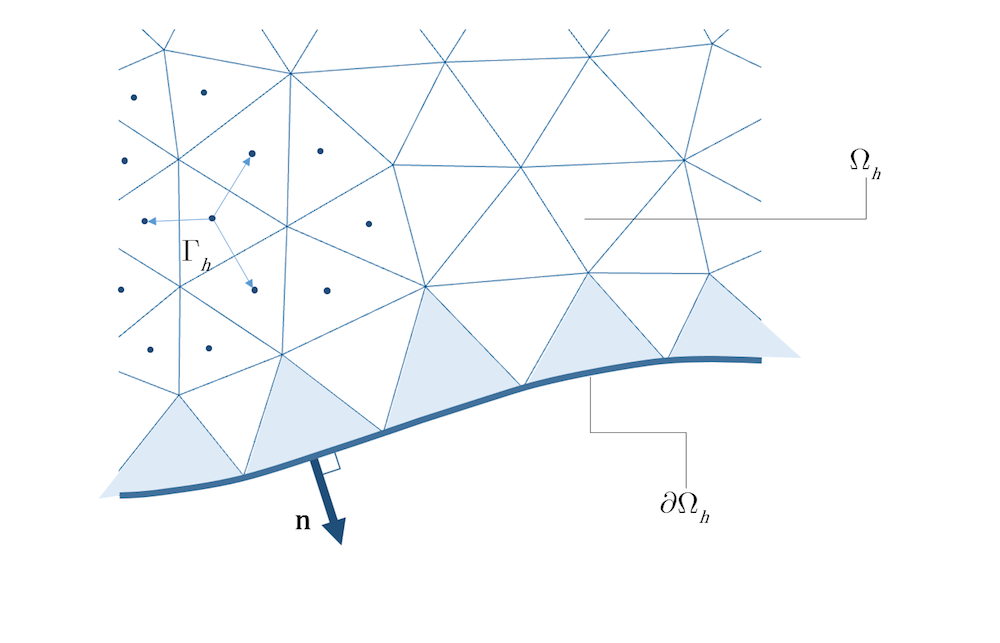
Рисунок 3. В центрированном по узлу МКО для расчёта вектора плотности потока используется интерполяция по значениям в центрах контрольных объёмов.
Меняя базисные функции в МКЭ и алгоритмы расчёта потоков в МКО, можно влиять на точность этих методов. Расчёт на грубой сетке с использованием метода второго порядка может оказаться более точным, чем применение метода первого порядка на мелкой сетке.
Как правило, метод конечных элементов, построенный на линейных пробных и базисных функциях, имеет второй порядок аппроксимации. МКЭ более гибок при выборе порядка дискретизации. Например, довольно просто можно перейти к квадратичным базисным функциям. Кроме того, не требуется строить интерполяционные соотношения для поиска решения. Этот метод очень симметричен, а граничные условия для плотности потока на внешних границах учитываются непосредственным образом.
Недостатком МКЭ, построенном на основе непрерывных пробных и базисных функций, является отсутствие свойства локальной консервативности; выполнение законов сохранения гарантируется только на глобальном масштабе. Другими словами, балансовые уравнения выполняются только для полного потока, проходящего через внешние границы области. Ещё один недостаток состоит в невозможности контролировать локальные потоки, вследствие чего требуется привлечение специальных алгоритмов стабилизации для решения уравнений дискретного аналога при наличии конвективного переноса. В данном случае стабилизация решения — это удаление нефизичных осцилляций, возникающих вследствие дискретизации. С помощью непосредственного изменения слабой формы уравнений или за счёт изменения пробных функций можно решить как проблему отсутствия локальной консервативности, так и проблему стабилизации решения в задачах с преобладанием конвективного переноса. Однако такие изменения могут привести к дополнительным затратам вычислительных ресурсов.
Мы уже отмечали выше, что метод контрольного объёма соответствует методу конечных элементов, построенному с использованием кусочно-постоянных базисных функций и интерполяционных соотношений более высокого порядка для расчёта потоков. Таким образом, эти методы имеют первый или второй порядок аппроксимации. Привлекательной особенностью метода контрольного объёма является локальное выполнение законов сохранения. Локальная консервативность означает, что для каждого контрольного объёма гарантируется соблюдение баланса полного потока. Кроме того, это свойство позволяет использовать простые и естественные методы стабилизации численной схемы в задачах гидродинамики с доминирующим преобладанием конвекции. Схема «против потока» и другие алгоритмы стабилизации получаются естественным образом при изменении способа расчёта плотности потока на гранях контрольных объёмов. Схема «против потока» приводит к нарушению симметрии дискретного аналога в направлении конвекции.
Метод конечных элементов можно построить на основе базисных функций разного порядка, и в этом состоит преимущество данного метода. Использование базисных функций более высокого порядка позволяет повысить порядок аппроксимации и создать более точные методы дискретизации, что является очень важной особенностью, позволяющей повысить точность решения на заданной расчётной сетке. В МКО используются базисные функции нулевого порядка, что компенсируется применением схем интерполяции более высокого порядка для расчёта потоков, а это также позволяет улучшить точность решения. Применение методов дискретизации высокого порядка приводит к увеличению размера итоговой системы уравнений, а следовательно, и время расчёта увеличивается даже при решении задачи на одной и той же сетке. Однако, то же самое происходит и при повышении порядка аппроксимации. Таким образом, эффективность методов имеет смысл сравнивать только для некоторого заданного значения точности. Адекватным способом оценки эффективности этих методов является измерение процессорного времени и объёма оперативной памяти, необходимых для решения гидродинамической задачи, но при этом идентичным должен быть критерий точности решения, а вовсе не число сеточных элементов или ячеек.
Будущее метода конечных элементов
В COMSOL для решения задач вычислительной гидродинамики мы преимущественно используем метод конечных элементов, поскольку мы имеем богатый опыт применения данного метода. За последние 15 лет исследовательское сообщество добилось значительных успехов в разработке метода конечных элементов, построенного на основе разрывных пробных и базисных функций. Это так называемые разрывные методы Галёркина (DG-FEM). Здесь используются локально заданные пробные функции, а слабая форма уравнений записывается для каждого элемента области. В результате условие локальной консервативности выполняется автоматически, а переход к схемам дискретизации более высокого порядка не представляет сложности. Нет необходимости и в реконструкции решения, которая нужна только при нулевом порядке дискретизации, при котором разрывный МКЭ становится эквивалентен МКО. Кроме того, локальная плотность потока на границе элемента остаётся естественным элементом слабой формы, что упрощает стабилизацию численной схемы. К недостаткам разрывного метода Галёркина можно отнести появление относительно большого числа дополнительных степеней свободы. Этого недостатка лишены так называемые гибридные разрывные методы Галёркина, в которых схема дискретизации более компактная, а значит вводится меньше дополнительных степеней свободы.
Заключительные мысли о МКЭ и МКО
В этой заметке блога мы постарались показать, что и МКЭ, и МКО имеют определённые достоинства и недостатки. А эффективность решения крупномасштабных задач гидродинамики определяется эффективностью множества других алгоритмов: корректировки временного шага; реализации неявной и, в некоторых случаях, явной схем интегрирования по времени, решения больших систем алгебраических уравнений и так далее. Впереди ещё много работы и огромный спектр возможностей для развития различных методов и технологий!
Мы в COMSOL непрерывно работаем над тем, чтобы предоставить пользователям наилучшие и самые современные инструменты численного моделирования на основе метода конечных элементов. Кроме того, мы стремимся разрабатывать и реализовывать самые эффективные методы не только для мультифизических задач, но и для узких физических приложений, например, для вычислительной гидродинамики.

