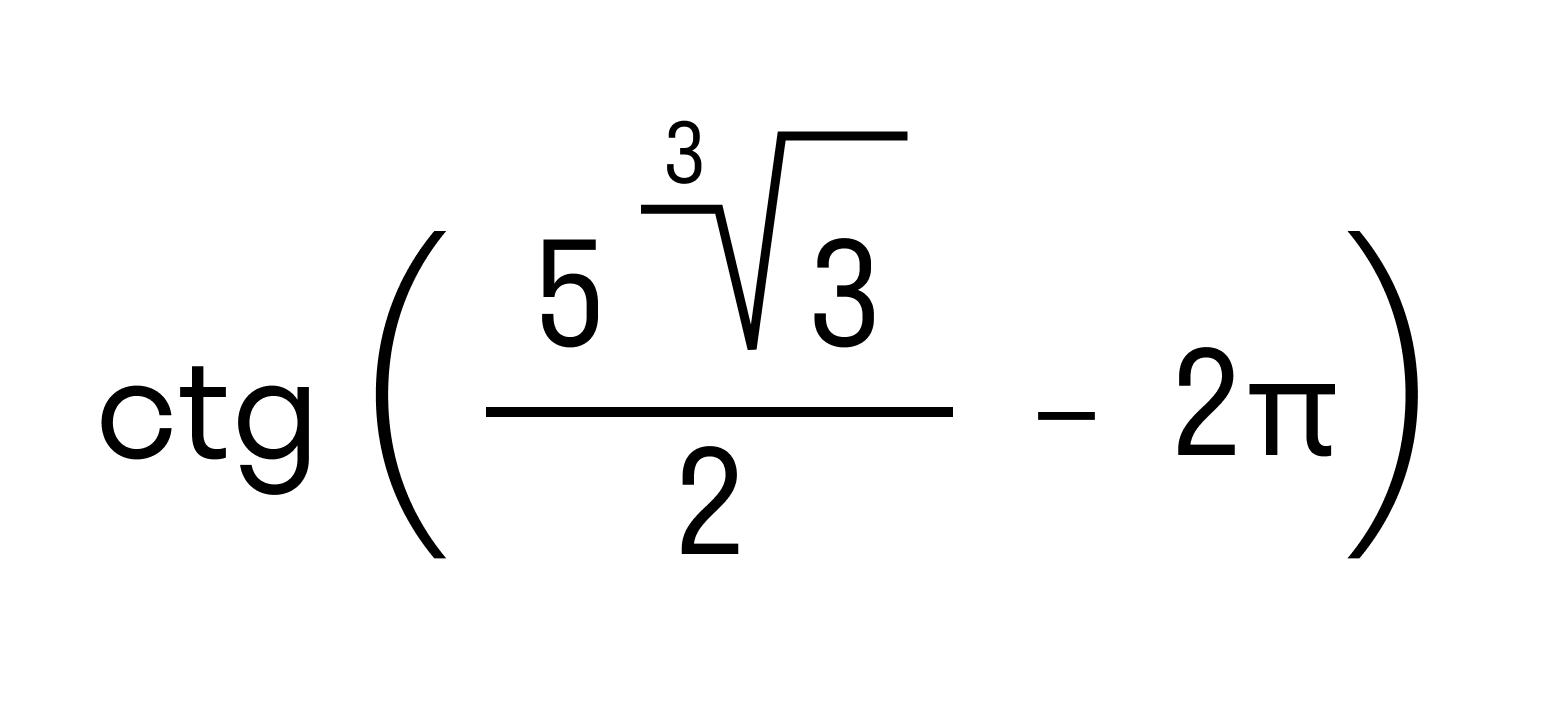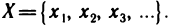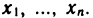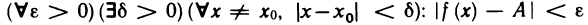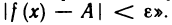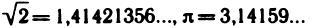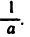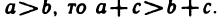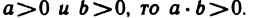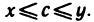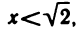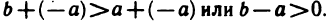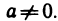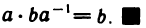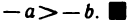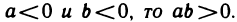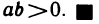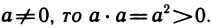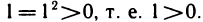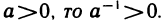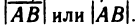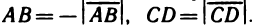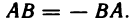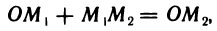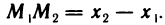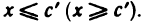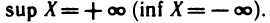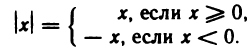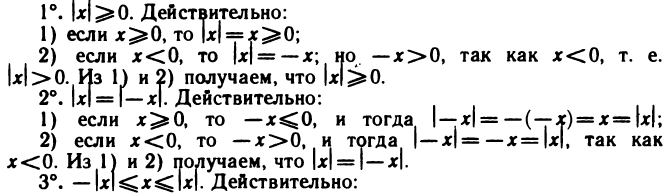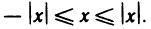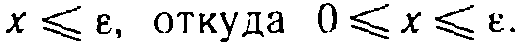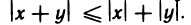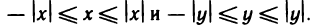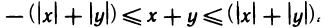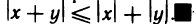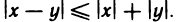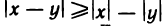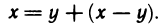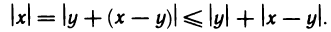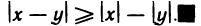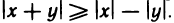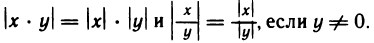Множество действительных чисел что это такое
Действительные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение действительных чисел
Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —
Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —
Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:
Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.
Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.
Примеры действительных чисел:
Число нуль также является действительным числом, так как 0 — рациональное число.
Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.
При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.
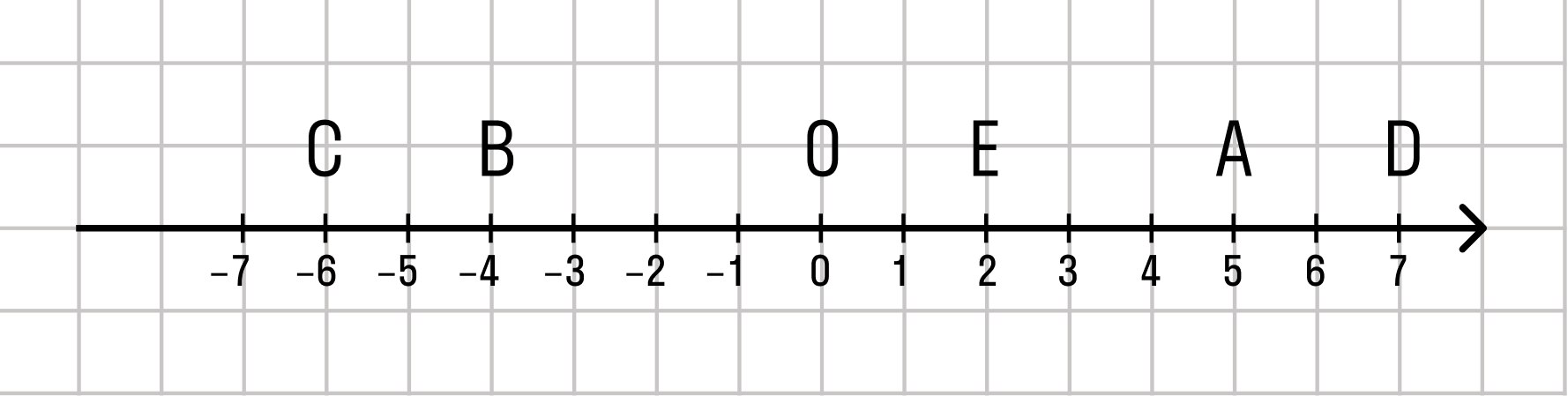
Действительные числа на координатной прямой
Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Интересный факт: действительные числа заполняют каждую точку координатной прямой.
Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Представления действительных чисел
По определению действительными числами являются:
Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.
Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений
будут действительные числа.
Сравнение действительных чисел
Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:
Вещественные числа в математике с примерами решения и образцами выполнения
Вещественные или действительные числа — это математическая абстракция, используемая для представления и сравнения значений физических величин. Чаще всего такое число представляют как описывающее положение точки или прямой. Множество вещественных чисел обозначается буквой R, которую нередко называют вещественной прямой.
Множества и обозначения. Логические символы
Понятие множества является одним из основных в математике. Оно принадлежит к так называемым первичным, неопределяемым понятиям. Слова «совокупность», «семейство», «система», «набор» и т. п. — синонимы слова «множество». Примерами множеств могут служить множество студентов данной аудитории; совокупность тех из них, кто сдал вступительные экзамены без троек; семейство звезд Большой Медведицы; система трех уравнений с тремя неизвестными; множество всех целых чисел и т. д. Из приведенных примеров следует, что множество может содержать конечное или бесконечное число произвольных объектов.
Объекты, из которых состоит множество, называются его элементами или точками. Множества часто обозначают большими, а их элементы — малыми буквами. Если х — элемент множества X, то пишут 
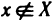
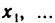
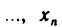
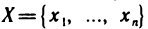
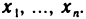
Пусть X и У — два множества. Если X и У состоят из одних и тех же элементов, то говорят, что они совпадают, и пишут X=Y. Если в X нет элементов, не принадлежащих У, то говорят что X содержится в У или что X — подмножество множества У. В этом случае пишут 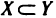
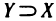
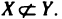

В дальнейшем нам придется иметь дело с различными множествами вещественных чисел*. Всюду, где это не может привести к неточности, для краткости вещественные числа будем называть просто числами.
* Вместо термина «вещественные числа» часто используют термин «действительные числа».
Пусть Р (х) — какое-то свойство числа х. Тогда запись 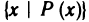
означает множество всех таких чисел, которые обладают свойством
Р(х). Например, множество 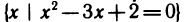
корней уравнения 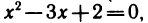
двух элементов: 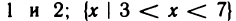

Если 
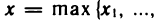
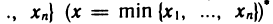
В математических предложениях (формулировках определений, теорем и т. д.) часто повторяются отдельные слова и целые выражения. Поэтому при их записи полезно использовать экономную логическую символику.
Здесь мы укажем лишь несколько самых простых и употребительных логических символов. Вместо слова «существует» или «найдется» используют символ 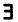

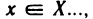

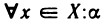
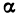
Для облегчения понимания и чтения утверждений, записанных с помощью логических символов, все, что относится только к каж- каждому из них, заключают в круглые скобки. Так, например, запись
читается так: «для любого 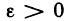
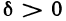
всех х, не равных хо и удовлетворяющих неравенству 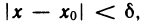
Символ 
Вещественные числа и их основные свойства
В курсе элементарной математики дается некоторое представление о вещественных числах. Из этого курса известно, что множество
вещественных чисел состоит из рациональных и иррациональных
чисел. Рациональным называется число, которое можно представить в виде p/q, где р и q — целые числа, причем 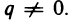
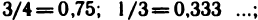
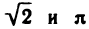
Систематизируем сведения о вещественных числах, перечислим основные свойства вещественных чисел, а затем выведем из них некоторые следствия.
Сложение и умножение вещественных чисел
Для любой пары а и b вещественных чисел определены и притом единственным образом два вещественных числа 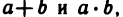
1°. 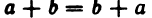
2°. 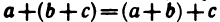
3°. 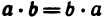
4°. 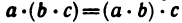
5°. 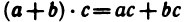
6°. Существует единственное число 0 такое, что а + 0=а для любого числа а.
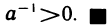
7°. Для любого числа а существует такое число (—а), что а+(-а) = 0.
8°. Существует единственное число 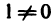
9°. Для любого числа 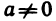
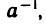
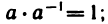
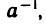
Сравнение вещественных чисел
Для любых двух вещественных чисел а и b установлено одно из отношений: а=b (а равно b), а>b (а больше b) или b>а. Отношение = обладает свойством: если а=b и b=с, то а=с.
Отношение > обладает следующими свойствами. Каковы бы ни были числа а, b и с:
10°. Если
11°. Если
12°. Если
Непрерывность вещественных чисел
13°. Пусть X и Y — два множества, состоящие из вещественных чисел. Тогда, если для любых чисел 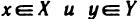
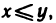
Отметим, что свойством непрерывности обладает множество всех
вещественных чисел, но не обладает множество только рациональных чисел. Действительно, пусть множество X состоит из рациональных чисел х, для которых выполняется неравенство
а множество У состоит из рациональных чисел у, для которых выполняется неравенство 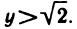
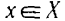
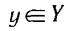

не существует рационального числа с такого, чтобы для всех таких
х и у выполнялись неравенства 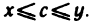
числом могло бы быть только 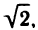
рациональным.
Из свойств I, II, III вытекают все остальные свойства вещественных чисел. Познакомимся лишь с некоторыми из них, но в дальнейшем будем использовать и другие, не проводя их формального доказательства.
Каковы бы ни были числа а, b, с и d:
14°. Число 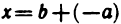
Действительно, согласно свойствам 1°, 2°, 6°, 7° имеем: а+b+(-a)=b.
Число b+(-a) называется разностью чисел b и а и обозначается b — а. Отметим, что если а а), то
разность b — а>0. В самом деле, из неравенства b>а в силу 11°
получаем:
15°. Число 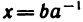
Действительно, согласно свойствам 3°, 4°, 8°, 9° имеем:
В самом деле, так как а 0. Следовательно, на
основании свойства 11° b-а+(-b)>0 + (-b), откуда полу-
получаем:
17°. Если а>b и с>d, то a+c>b+d.
В самом деле, если а>b и c>d, то в силу свойства 11° а+c>b+c и c+b>d+b. Поэтому согласно свойству 10° а+с>b+d.
24°. Если
В самом деле, так как 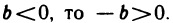
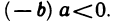
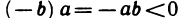
25°. Если
Справедливость данного утверждения следует из свойств 12° и 24°. В частности,
26°. Если
В самом деле, согласно свойствам 9° и 25° 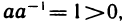
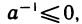
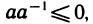
Итак, мы видим, что из основных свойств I—III вещественных чисел вытекают остальные их свойства. Поэтому можно сказать, что вещественные числа представляют собой множество элементов, обладающих свойствами I—III. Такое определение вещественных чисел называется аксиоматическим, а свойства I—III — аксиомами вещественных чисел.
В заключение отметим, что, исходя из свойств I—III, любое вещественное число можно представить в виде бесконечной десятичной дроби. Однако останавливаться на рассмотрении этого вопроса не будем.
Геометрическое изображение вещественных чисел
Изображение вещественных чисел точками на координатной прямой
Введем ряд предварительных понятий. Рассмотрим произвольную прямую. На ней можно указать два взаимно противоположных направления. Выберем одно из них и на рисунке будем обозначать его стрелкой (рис. 1). Пусть, кроме того, выбрана масштабная единица для измерения длин отрезков. Прямая с выбранным на ней направлением называется осью.
Рассмотрим на оси две произвольные точки Л и В. Отрезок с граничными точками Л и В будем называть направленным, если указано, какая из точек Л и В считается началом, а какая — кон-
концом отрезка. Направленный отрезок с началом в точке А и концом в точке В обозначим 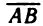
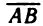
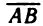
Для направленных отрезков, лежащих на оси (или параллель-
параллельных оси), вводится понятие величины направленного отрезка. Величиной АВ направленного отрезка 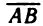
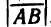
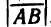
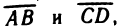
Заметим, что величины направленных отрезков 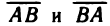
любом направлении оси отличаются знаками:
Если точки А и В совпадают, то величину направленного отрезка 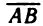
Для любых трех точек А, В и С на оси справедливо равенство
АВ + ВС = АС,
которое назовем основным тождеством (в дальнейшем оно неоднократно используется).
Справедливость основного тождества легко устанавливается из
рисунка, но при этом нужно рассмотреть различные случаи взаимного расположения точек А, В и С на оси. Если все три точки А,
В и С различны, то таких случаев шесть (рис. 3). В каждом из этих
случаев основное тождество проверяется элементарно.
Перейдем теперь к геометрическому изображению вещественных
чисел. Рассмотрим какую-нибудь прямую. Выберем на ней направление (тогда она станет осью) и некоторую точку О (начало
координат). Прямую с выбранным направлением и началом координат назовем координатной прямой (считаем, что масштабная единица выбрана). Пусть М — произвольная точка на прямой (рис. 4, а).
Поставим в соответствие точке М число х, равное величине ОМ
направленного отрезка 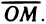
точки М. Тем самым каждой точке координатной прямой будет
соответствовать определенное вещественное число — ее координата. Справедливо и обратное: каждому вещественному числу х
соответствует некоторая точка на координатной прямой, а именно
такая точка М, координата которой равна х.
Таким образом, вещественные числа можно изображать точками
на координатной прямой. Поэтому около точки на координатной
прямой часто указывают число —ее координату (рис. 4, б).
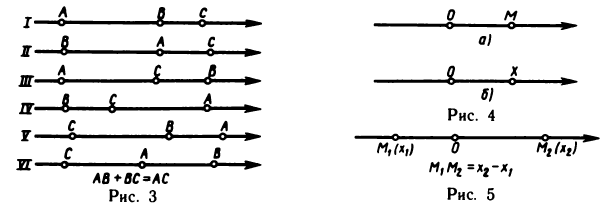
Пусть точка 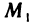
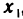
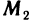
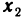
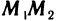
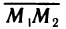
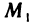
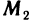
откуда 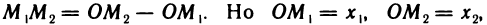
Эту формулу будем часто использовать в аналитической геометрии.
Некоторые наиболее употребительные числовые множества
Пусть а и b — два числа, причем а Грани числовых множеств
Говорят, что. множество X ограничено сверху (снизу), если существует число с такое, что для любого 
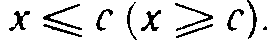
Множество, ограниченное и сверху и снизу, называется ограниченным.
Так, например, любой конечный промежуток 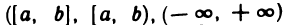
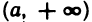
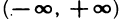
Очевидно, что любое ограниченное сверху (снизу) множество X имеет бесконечно много верхних (нижних) граней. В самом деле, если число с является верхней (нижней) гранью множества X, то любое число с’, большее (меньшее) числа с, — также верхняя (нижняя) грань множества X, так как из справедливости неравенства 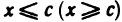
Естественно, возникает вопрос о существовании наименьшей из верхних граней ограниченного сверху множества и наибольшей из нижних граней ограниченного снизу множества.
Наименьшая из верхних граней ограниченного сверху множества X называется точной верхней гранью множества X и обозначается символом sup X, а наибольшая из нижних граней ограниченного снизу множества X называется точной нижней гранью этого множества и обозначается символом inf X*.
Примеры:
Пусть 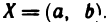
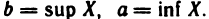
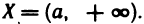
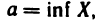
Точная верхняя грань (sup X) обладает следующим важным свойством. Как бы мало ни было число 

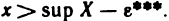
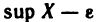
Отмеченное свойство точной верхней грани можно переформулировать следующим образом: если с = sup X, то для любого числа с’ 0, найдется 
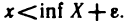
Возникает вопрос, всегда ли ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань. Ответ на этот вопрос дает следующая важная теорема.
Теорема:
Любое непустое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.
Доказательство:
Пусть X — непустое множество, ограниченное сверху. Тогда множество У чисел, ограничивающих X сверху, не пусто. Из определения верхней грани следует, что для любого 
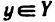

Из первого из неравенств (1) следует, что число с ограничивает множество X сверху, т..е. является верхней гранью, а из второго, — что оно наименьшее из таких чисел, т. е. является точной верхней гранью.
Случай существования точной нижней грани у не пустого ограниченного снизу множества рассматривается аналогично.
Если множество X не ограничено сверху (снизу), то условимся писать:
Абсолютная величина числа
Понятие абсолютной величины числа и неравенства, связанные с абсолютными величинами, в дальнейшем часто используются.
Определение:
Абсолютной величиной (или модулем) числа х называется само число х, если 
Абсолютная величина числа х обозначается символом |х|. Таким образом,
Из определения вытекает ряд свойств абсолютной величины числа.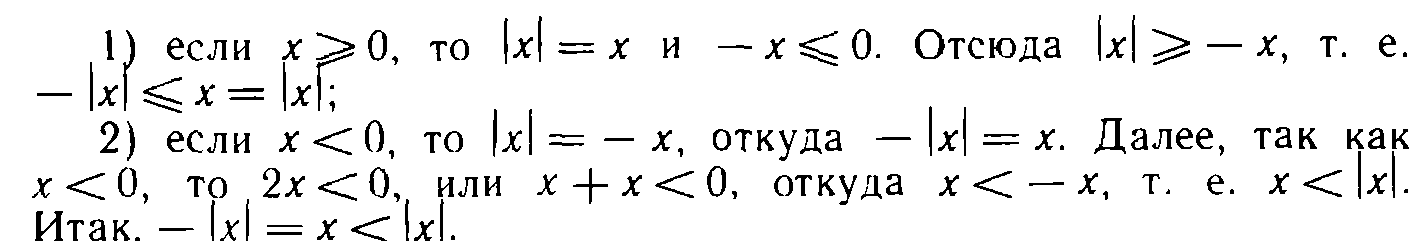
Поскольку следующие три свойства очень важны, докажем их в виде теорем.
Теорема:
Пусть 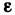
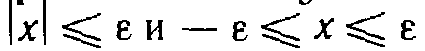
Доказательство:
Пусть 
1) если 
2) если 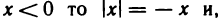
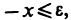
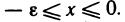
Пусть справедливы неравенства 
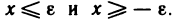
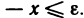
Теорема:
Абсолютная величина суммы двух чисел не больше суммы абсолютных величин этих чисел, т. е.
Доказательство:
Пусть х и у — любые числа. Согласно свойству 3° для них справедливы неравенства
Складывая их почленно, получаем
По теореме 1.2 это двойное неравенство равносильно неравенству
Заметим, что
Теорема:
Абсолютная величина разности двух чисел не меньше разности абсолютных величин этих чисел, т. е.
Доказательство:
Для любых чисел х и у имеем
По теореме 1.3 справедливо неравенство
Откуда получаем:
Заметим, что
В заключение отметим, что каковы бы ни были два числа х и у, имеют место легко проверяемые соотношения:
Свойства вещественных чисел


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института