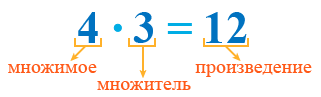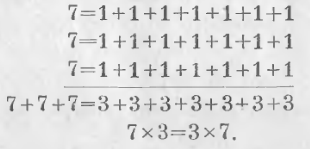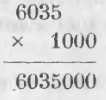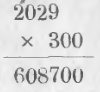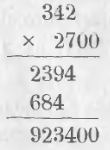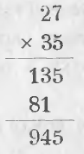Множимое множитель что получится
Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
Числа при умножении
Результат умножения, или Произведение
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
Заменяем сложение умножением и получаем:
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Учимся дома 1-11 классы
Заметки о семейном образовании
Умножение. Как объяснить ребёнку?
Умножение. Как объяснить ребёнку? Просто!
Умножение — это то же самое сложение. Только упрощённое. Не верите? Ну, как же! Смотрите сами…
2+2+2+2+2+2+2+2+2+2+2+2=.
Это же пока сосчитаешь, сколько тут двоек, да сложишь все по очереди! Тут и пенсия как раз настанет!
2 х 12 = 24 и всё!
И для облегчения счёта создана таблица умножения. Один раз выучил — всю жизнь пользуешься. Очень удобно!
Сначала дети учатся умножать и запоминают, как называются числа при умножении. Кажется, всё просто. Аналогично сложению. Там были слагаемые и сумма, тут множители и произведение.
Странные исправления в задачах
Засада начинается позже, когда начинаются задачи. Все помнят эти фотографии из родительских чатов с вопросами: За что? И почему так?
На фото было что-то типа такого:
В чём же дело?
Ведь всем же ясно, что 3х2, что 2х3 — получится одинаковое число. За что издеваются над нашими детьми?
Всё дело в логике.
Если пишем 3 х 2, то по условию задачи получаем: три раза мальчик нарисовал по 2 кораблика.
Если пишем 2 х 3, то получаем: по 2 кораблика мальчик нарисовал три раза.
Ну и что? Хрен редьки не слаще! Что в лоб, что по лбу! Разница-то в чём?
Тем более, что в старших классах дети всё равно будут учить переместительный закон умножения: от перемены мест множителей сумма не меняется.
Вот раньше таких проблем не было!
Действительно, не было!
А дело всё в том, что числа при умножении назывались иначе. Вернее, одно число называлось иначе и всё становилось на свои места!
И никто не путался. Сразу же ясно:
И задача сразу иначе звучит. Решать ее надо иначе.
Сразу следует подумать, о чём идёт речь в задаче?
О корабликах! Сколько было корабликов? Два. Два — это множимое!
Во сколько раз больше Вася нарисовал корабликов? В три! Три — это множитель!
Отсюда: верная запись: 2 х 3 = 6 (и никак иначе!)
А как же может звучать вопрос при умножении?
А теперь давайте тренироваться!
Тест на умножение. Если Вы его не видите, значит его блокирует какая-то программа, установленная на Вашем компьютере. Обычно, блокировщик рекламы.
Умножение натуральных чисел
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
Сократим запись, заменив сложение на умножение:
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.
Правила умножения натуральных чисел
Что такое умножение
Умножение — такое арифметическое действие, когда сложение одинаковых чисел происходит искомое количество раз.
Умножение имеет широкую матрицу для применения.
Множимое — число, которое будет использоваться в математическом действии.
Множитель — число раз, сколько нужно данное число (множимое) повторить, для выполнения операции.
Произведение — итог действия, результат математической операции.
Знак умножения в алгебре обозначается (∙) точкой в середине строки. Допустимо в печати использование крест (х), в компьютерной печати нередко используется звездочка (*).
Описание основных правил, порядок действий
Чтобы произвести умножение в алгебре, нужно помнить и понимать смысл самой математической операции.
25 х 4 = 25 + 25 + 25 + 25 = 100
Множимое число 25 умножаем на множитель 4 — понимаем это как сумма четырех чисел 25, или как сумма, где 25 сложили 4 раза. 100 — произведение арифметической операции.
При умножении на число с нулями (десять, сто, тысяча, десять тысяч, миллион) достаточно в произведении к множителю дописать нули.
Познакомимся с алгоритмом умножения в столбик. Это поможет в решении многих примеров, в том числе с дробями. Ученик действует по принципу пишу, затем умножаю единицы, затем десятки, наконец сотни.
Решите пример 25 ∙ 16 с помощью столбика.
Чтобы произвести умножение столбиком, действуем последовательно.
Законы с примерами, как проверить результат
В умножении, как и в делении, сложении и вычитании, есть свои нормы и порядки.
Переместительный закон умножения
От перестановки слагаемых сумма чисел не меняется. Этот же закон действует и для умножения. Если множитель и множимое поменять местами, полученное произведение чисел не изменится.
Переместительный закон гласит, что от перемены мест множителей произведение не меняется.
a ∙ b = b ∙ a
Разберем переместительный закон на примере задачи.
У садовника в трех корзинах было по 14 груш. Сколько всего было груш в корзинах?
Решение: 14 ∙ 3 = 42 (груши) или 3 ∙ 14 = 42 (груши).
Ответ: 42 груши у садовника было в корзинах.
В многоэтажном доме 75 квартир. В каждой квартире проживает 5 жильцов. Сколько всего жильцов в этом многоэтажном доме?
Решение: 75 ∙ 5 = 375 (жильцов) или 5 ∙ 75 = 375 (жильцов).
Ответ: 375 жильцов всего проживает в многоэтажном доме.
Сочетательный закон умножения
Сочетательный закон умножения объясняет, чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
a · b · c = (a · b) · c = a · (b · c)
То есть фактически при решении уравнения есть возможность менять множители местами. Воспользоваться этой формулой необходимо, например, когда операцию внутри скобок провести легче, чем предложенное прямое уравнение.
71 · 25 · 4 = 71 · (25 · 4) = 710
В данном случае найти произведение 25 · 4 не составит труда у школьников, тогда как умножение 71 на 25 довольно длительная и проблематичная операция.
Распределительный закон умножения
Распределительный закон умножения действует относительно двух других важных операций: сложение и вычитание.
а ∙ (b + c) = a ∙ b + a ∙ с
Если нужно умножить число на сумму чисел, допускается умножить число отдельно на каждое из этих чисел и затем произвести сложение.
5 ∙ (12 + 16) = 5 ∙ 28 = 140
5 ∙ 12 + 5 ∙ 16 = 60 + 80 = 140
Как мы можем убедиться из этого примера, при одинаковом произведении произвести операцию в данном случае через сумму отдельных произведений a ∙ b + a ∙ с проще.
а ∙ (b – c) = a ∙ b – a ∙ с
Для умножения числа на множитель, который представляет собой операцию вычитания, нужно умножить число отдельно на каждое из чисел в скобках, а затем произвести вычитание.
В данной арифметической операции к итогу 144 также можно прийти двумя способами. Решение примера по математике зависит от предложенных в задании компонентов и логической мысли ученика.
Математика
Умножить одно целое число на другое значит повторить одно число столько раз, сколько в другом содержится единиц. Повторить число значит взять его слагаемым несколько раз и определить сумму.
Определение умножения
Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.
Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.
Умножение есть сложение равных слагаемых.
Данные в умножении называются множимым и множителем, а искомое — произведением.
В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.
Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.
Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.
Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.
Множимое и множитель вместе называются производителями.
При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.
Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать
пишут при помощи знака умножения короче:
Умножение есть сокращенное сложение равных слагаемых.
Связь между данными и искомым числом выражается в умножении
7 × 3 = 21 или 7 · 3 = 21
семь, умноженное на три, составляет 21.
Чтобы составить произведение 21, нужно 7 повторить три раза
Чтобы составить множитель 3, нужно единицу повторить три раза
Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.
Основное свойство произведения
Произведение не изменяется от перемены порядка производителей.
Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:
Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.
Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.
Умножение однозначных чисел. Таблица Пифагора
Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения.
Таблица Пифагора. Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора. (Пифагор родился около 569 года до н. э.).
Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:
Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д. Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.
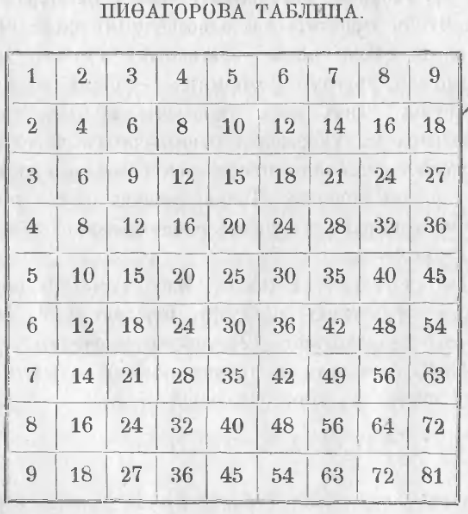
Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде
Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.
Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:
Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.
Умножение многозначного числа на однозначное
Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.
Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых
следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.
При этом ход вычислений выражают словесно:
Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).
Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.
Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.
Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.
Это действие выразится письменно:
Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:
Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.
Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.
Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.
Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.
Умножение продолжается до тех пор, пока не получат полного произведения.
Умножение чисел на 10, 100, 1000 …
Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.
Этого достигают, приписывая к числу два нуля.
Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.
Умножение числа 6035 на 1000 выразится письменно:
Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.
Умножение на число с нулями в конце
Чтобы умножить 2039 на 300 нужно взять число 2029 слагаемым 300 раз. Взять 300 слагаемых все-равно, что взять три раза по 100 слагаемых или 100 раз по три слагаемых. Для этого умножаем число на 3, а потом на 100, или умножаем сначала на 3, а потом приписываем справа два нуля.
Ход вычисления выразится письменно:
Правило. Чтобы умножить одно число на другое, изображаемое цифрой с нулями, нужно сначала помножить множимое на число, выражаемое значащей цифрой, и затем приписать столько нулей, сколько их находится в множителе.
Умножение многозначного числа на многозначное
Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.
называются частными произведениями.
Полное произведение 3029 × 429 равно сумме трех частных:
3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.
Найдем величины этих трех частных произведений.
Умножая 3029 на 9, находим:
Умножая 3029 на 20, находим:
Умножая 3026 на 400, находим:
Сложив эти частные произведения, получим произведение 3029 × 429:
Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.
Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:
В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.
Отыскивая произведение 3247 на 209, имеем:
Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.
Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.
Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,
нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.
Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.
Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.
Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.
Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.
Пример. Найти произведение 342 на 2700.
Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.
Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35
Приписывая к 945 пять нулей, получаем искомое произведение:
2700 × 35000 = 94500000.
Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).
Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.
В нашем произведении может содержаться или 7 или 6 цифр.
Степени
Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:
Квадраты. Произведение двух равных множителей называется квадратом числа.
В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.
Кубы. Произведение трех равных множителей называется кубом числа.
Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.
Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.
Произведения двух равных множителей или квадраты называются вторыми степенями.
Произведения трех равных множителей или кубы называются третьими степенями, и т. д.