Модуль что это такое в машиностроение
Модуль зубчатого колеса
Смотреть что такое «Модуль зубчатого колеса» в других словарях:
МОДУЛЬ ЗУБЧАТОГО КОЛЕСА — геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса. Различают осевой, окружной и нормальный модуль зубчатого колеса … Большой Энциклопедический словарь
модуль зубчатого колеса — отношение шага зубьев колеса (расстояние между соответствующими точками соседних зубьев, измеренное по дуге окружности) к числу π. Значения модуля зубчатого колеса стандартизованы. Геометрические размеры зубчатых колёс выбираются пропорционально… … Энциклопедический словарь
нормальный модуль зубьев конического зубчатого колеса — (mn) нормальный модуль Линейная величина, в раз меньшая нормального шага зубьев конического зубчатого колеса. Примечания 1. Различают нормальные модули: внешний (mne), средний (mnm), внутренний (mni) и др. (mnx) делительные; внешний (mnwe),… … Справочник технического переводчика
нормальный модуль цилиндрического зубчатого колеса — (mn) модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание В случаях, исключающих возможность возникновения недоразумений, индекс… … Справочник технического переводчика
окружной модуль зубьев конического зубчатого колеса — (mt) окружной модуль Линейная величина, в раз меньшая окружного шага зубьев конического зубчатого колеса. Примечание Различают окружные модули: внешний (mte), средний (mtm), внутренний (mti) и др. (mtx) делительные; внешний (mtwe), средний (mtwm) … Справочник технического переводчика
расчетный модуль конического зубчатого колеса — расчетный модуль Окружной или нормальный делительный модуль в расчетном сечении. Примечания 1. Расчетный модуль конического зубчатого колеса из семейства сопряженных конических зубчатых колес, форма и размеры зубьев которых определяются парой… … Справочник технического переводчика
Нормальный модуль цилиндрического зубчатого колеса т n — 2.1.2. Нормальный модуль цилиндрического зубчатого колеса т n Модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание. В случаях,… … Словарь-справочник терминов нормативно-технической документации
Нормальный модуль зубьев конического зубчатого колеса — 67. Нормальный модуль зубьев конического зубчатого колеса Нормальный модуль mn Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
Окружной модуль зубьев конического зубчатого колеса — 59. Окружной модуль зубьев конического зубчатого колеса Окружной модуль mt Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
Расчетный модуль конического зубчатого колеса — 146. Расчетный модуль конического зубчатого колеса Расчетный модуль Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Как узнать модуль зубчатого колеса?

. кому приходится восстанавливать зубчатые передачи при отсутствии рабочих чертежей на вышедшие из строя детали.
«Вооружаемся» штангенциркулем, угломером или хотя бы транспортиром, линейкой и программой MS Excel, которая поможет быстро выполнять рутинные и порой непростые расчеты, и начинаем работу.
Как обычно раскрывать тему я буду на примерах, в качестве которых рассмотрим сначала цилиндрическую прямозубую передачу с наружным зацеплением, а затем косозубую.
Расчетам зубчатых передач на этом сайте посвящено несколько статей: «Расчет зубчатой передачи», «Расчет геометрии зубчатой передачи», «Расчет длины общей нормали зубчатого колеса». В них приведены рисунки с обозначениями параметров, используемых в данной статье. Эта статья продолжает тему и призвана раскрыть алгоритм действий при ремонтно-восстановительных работах, то есть работах, обратных проектировочным.
Расчеты можно выполнить в программе MS Excel или в программе OOo Calc из пакета Open Office.
О правилах форматирования ячеек листа Excel, которые применены в статьях этого блога, можно прочитать на странице « О блоге ».
Расчет параметров колеса и шестерни прямозубой передачи.
Изначально полагаем, что зубчатое колесо и шестерня имеют эвольвентные профили зубьев и изготавливались с параметрами исходного контура по ГОСТ 13755-81. Этот ГОСТ регламентирует три главных (для нашей задачи) параметра исходного контура для модулей больше 1 мм. (Для модулей меньше 1 мм исходный контур задается в ГОСТ 9587-81; модули меньше 1 мм рекомендуется применять только в кинематических, то есть не силовых передачах.)
Для правильного расчета параметров зубчатой передачи необходимы замеры и шестерни и колеса!
Исходные данные и замеры:
Начинаем заполнение таблицы в Excel с параметров исходного контура.
1. Угол профиля исходного контура α в градусах записываем
2. Коэффициент высоты головки зуба ha* вводим
3. Коэффициент радиального зазора передачи c* заносим
В СССР и в России 90% зубчатых передач в общем машиностроении изготавливались именно с такими параметрами, что позволяло применять унифицированный зубонарезной инструмент. Конечно, изготавливались передачи с зацеплением Новикова и в автомобилестроении применялись специальные исходные контуры, но все же большинство передач проектировалось и изготавливалось именно с контуром по ГОСТ13755-81.
4. Тип зубьев колеса (тип зацепления) T записываем
T =1 – при наружных зубьях у колеса
T =-1 – при внутренних зубьях у колеса (передача с внутренним зацеплением)
5. Межосевое расстояние передачи a w в мм измеряем по корпусу редуктора и заносим значение
Ряд межосевых расстояний зубчатых передач стандартизован. Можно сравнить измеренное значение со значениями из ряда, который приведен в примечании к ячейке C7. Совпадение не обязательно, но высоковероятно.
Обращаю внимание: углы наклона зубьев βa1 и βa2 – это углы, измеренные на цилиндрических поверхностях вершин зубьев.
Измеряем диаметры, по возможности, максимально точно! Для колес с четным числом зубьев сделать это проще, если вершины не замяты. Для колес с нечетным числом зубьев при замере помним, что размеры, которые показывает штангенциркуль несколько меньше реальных диаметров выступов. Делаем несколько замеров и наиболее с нашей точки зрения достоверные значения записываем в таблицу.
Результаты расчетов:
14. Предварительные значения м одуля зацепления определяем по результатам замеров шестерни m1 и зубчатого колеса m2 в мм соответственно
в ячейке D17: =D9/(D8/COS (D20/180*ПИ())+2*D4) =2,089
и в ячейке D18: =D13/(D12/COS (D21/180*ПИ())+2*D4) =2,005
Модуль зубчатого колеса играет роль универсального масштабного коэффициента, определяющего как габариты зубьев, так и общие габариты колеса и шестерни.
Сравниваем полученные значения со значениями из стандартного ряда модулей, фрагмент которого приведен в примечании к ячейке C19.
Полученные расчетные значения, как правило, очень близки к одному из значений стандартного ряда. Делаем предположение, что искомый модуль зубчатого колеса и шестерни m в мм равен одному из этих значений и вписываем его
15. Предварительные значения у гла наклона зубьев определяем по результатам замеров шестерни β 1 и зубчатого колеса β 2 в градусах соответственно
в ячейке D20: =ASIN (D8*D19/D9*TAN (D11/180*ПИ())) =0,0000
и в ячейке D21: =ASIN (D12*D19/D13*TAN (D15/180*ПИ())) =0,0000
Делаем предположение, что искомый угол наклона зубьев β в градусах равен измеренным и пересчитанным значениям и записываем
в ячейку D22: 0,0000
16. Предварительные значения коэффициента уравнительного смещения вычисляем по результатам замеров шестерни Δy 1 и зубчатого колеса Δy2 соответственно
в ячейке D23: =2*D4+D5- (D9-D10)/(2*D19) =0,025
и в ячейке D24: =2*D4+D5- (D13-D14)/(2*D19) = 0,025
Анализируем полученные расчетные значения, и принятое решение о значении коэффициента уравнительного смещения Δy записываем
17,18. Делительные диаметры шестерни d1 и зубчатого колеса d2 в мм рассчитываем соответственно
в ячейке D26: =D19*D8/COS (D22/180*ПИ()) =32,000
и в ячейке D27: =D19*D12/COS (D22/180*ПИ()) =126,000
19. Делительное межосевое расстояние a в мм вычисляем
в ячейке D28: =(D27+D6*D26)/2 =79,000
20. Угол профиля αt в градусах рассчитываем
в ячейке D29: =ATAN (TAN (D3/180*ПИ())/COS (D22/180*ПИ()))/ПИ()*180 =20,0000
21. Угол зацепления αtw в градусах вычисляем
в ячейке D30: =ACOS (D28*COS (D29/180*ПИ())/D7)/ПИ()*180 =21,8831
22,23. Коэффициенты смещения шестерни x1 и колеса x2 определяем соответственно
24,25. Коэффициент суммы (разности) смещений xΣ(d) вычисляем для проверки правильности предыдущих расчетов по двум формулам соответственно
в ячейке D33: =D31+D6*D32 =0,525
и в ячейке D34: =(D12+D6*D8)*((TAN (D30/180*ПИ()) — (D30/180*ПИ())) — (TAN (D29/180*ПИ()) — (D29/180*ПИ())))/(2*TAN (D3/180*ПИ())) =0,523
Значения, рассчитанные по разным формулам, отличаются очень незначительно! Полагаем, что найденные значения модуля зубчатого колеса и шестерни, а также коэффициентов смещения определены верно!
Расчет параметров колеса и шестерни косозубой передачи.
Переходим к примеру с косозубой передачей и повторяем все действия, которые мы делали в предыдущем разделе.
Измерить угол наклона зубьев с необходимой точностью при помощи угломера или транспортира практически очень сложно. Я обычно прокатывал колесо и шестерню по листу бумаги и затем по отпечаткам транспортиром делительной головки кульмана производил предварительные измерения с точностью в градус или больше. В представленном ниже примере я намерил: βa1 =19° и βa2 =17,5°.
Еще раз обращаю внимание, что углы наклона зубьев на цилиндре вершин βa1 и βa2 – это не угол β , участвующий во всех основных расчетах передачи. Угол β – это угол наклона зубьев на цилиндре делительного диаметра (для передачи без смещения).
Ввиду малости значений рассчитанных коэффициентов смещения уместно предположить, что передача была выполнена без смещения производящих контуров шестерни и зубчатого колеса.
Воспользуемся сервисом Excel «Подбор параметра». Подробно и с картинками об этом сервисе я в свое время написал здесь.
Выбираем в главном меню Excel «Сервис» — «Подбор параметра» и в выпавшем окне заполняем:
Передача, скорее всего, была выполнена без смещения, модуль зубчатого колеса и шестерни, а также угол наклона зубьев мы определили, можно делать чертежи!
Важные замечания.
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.
Не забывайте подтверждать подписку кликом по ссылке в письме, которое тут же придет к вам на указанную почту (может прийти в папку «Спам»).
Уважаемые читатели! Ваш опыт и мнение, «оставленные» ниже в комментариях к статье, будут интересны и полезны коллегам и автору.
Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).
Статьи с близкой тематикой
Отзывы
30 комментариев на «Как узнать модуль зубчатого колеса?»
Всегда возникают определённые трудности при вычислении модуля а особенно угла наклона зуба, если зубья почти отсутствуют. Спасибо.
Так ведь можно шаг разделить на пи и получим модуль.
А как его (шаг) измерить на делительном диаметре? На реальном колесе он (диаметр) не нарисован и при сильной коррекции вообще иногда находится вне тела детали. Да статья не только о модуле и не столько о модуле. Кто восстанавливал чертежи по обломкам косозубых сильно коррегированных колес меня поймет.
Юрий, напишите внутренние диаметры колеса и шестерни. И все замеры желательно сделать с точностью 0,1мм.
Файл с решением задачи отправлен на Ваш e-mail.
ну не совсем эта таблица поможет. а если не все данные можно замерить. если зубья схавало и пойми какие они были норомальные или с коррекцией, с одной муфтой очень долго мучался колличество зубьев известно сопригаемой шестерни тоже это был панетарный редуктор, долго голову ломал в расчетах типо все работае на практике нет. пришлось методо проб ишибок изготовить три разные муфты, в итоге оказалось что визуально не отлечишь какой зуб редуктор был германский и технология хер пойми какая применялась для нарезания зуба у меньшил количество зуба на 1 и все завелось но несчиталось при этом по нашим гостам. особо не обольщайтесь может такое случится с каждым.
Если разбить в хлам валы, шестерни, корпус и потом все переплавить для верности, то представленная в статье программа точно не поможет. Обольщаться не буду, обещаю. Чего только не может случиться с каждым. 🙂
Ребят, ну понятно, что это не универсальная программа. И что буржуи выжимают из железа по максимуму. И что достигается это в том числе глубокой коррекцией.
А автору большой такой респект за культивацию знаний и освежение памяти старым техническим кадрам, к которым я себя то же причисляю.
Здравствуйте. Классная статья. Спасибо за труды. Прочитав статью возник вопрос. Я работаю на ЧПУ станке, самоучкой. И для изучения параметрического программирования пытаюсь сделать универсальную программу для велосипедных звезд. Все получается, кроме радиуса от кривой впадины к вершине зуба. От диаметра звезды меняется профиль зуба. Помогите, если сможете. Есть ли формула по которой это рассчитывается. Коллеги на работе говорят, что подобное уже кто-то делал, но программа и все записи утеряны, а тот кто писал программу уже не работает. И там все сводилось к изменению одного коэффициента.
Здравствуйте, Руслан. У меня в планах есть эта тема.
А пока могу только отослать к ГОСТ 591-69 (в ред. 1989г.)/есть формулы для построения ПРАВИЛЬНОГО профиля зубьев звездочек и во 2-ом томе справочника Анурьева/. Искомая Вами кривая — это дуги окружности.
Здравствуйте! Интересная статья, то же с удовольствием освежил память. Хотелось бы почитать про расчёт питчевой косозубой шестерни. Есть у Вас такие наработки?
Добрый день, Николай. Расчет питчевых зубчатых передач ничем особенным не отличается от модульных. Эвольвента она и есть эвольвента. Нормальный исходный контур может иметь другие параметры, например, угол может быть не 20 градусов. Это означает, что инструмент придется заказывать или изготавливать не стандартный. Ну и модуль будет не из стандартного ряда и не «круглым» числом. Для автоматизированного расчета геометрии зубчатой передачи в Excel это никакого значения не имеет.
Извините, но Ваш файл не открывается. В чем может быть причина?
С уважением Анатолий.
Проверил. Всё открывается.
Может у Вас нет программы Excel на компьютере? Попробуйте открыть бесплатной программой Calc из OpenOffice или из LibreOffice (я попробовал — открывается корректно и даже с сохранением форматирования).
Здравствуйте, Александр! Присоединяюсь к числу благодарных читателей! Есть небольшой опыт в проектировании простых прямозубых п-ч. Помогите, как именно высчитать утерянную шестерню (редуктор ГДР). есть межосевое 34,5мм,колесо da=61,2мм, 70зуб., модуль,вроде,1 и угол наклона зуба 18,5градусов.
Здравствуйте, Александр! Помогите,пожалуйста, с решением проблемы! Утеряна шестерня. Есть: межосевое 34,5мм. Колесо: da=61,2мм, 70зуб.,модуль,вроде,1мм, угол наклона зубьев 18,5. Редуктор ГДР.
Для решения вашей проблемы нужно знать:
1. Какой диаметр впадин (желательно измерить на микроскопе до 0.1 мм)?
2. Наружный — тоже по-точнее.
3. Угол наклона зубьев на окружности выступов. Угол наклона как измеряли? Расчетный — тот на делительном диаметре.
Углом и/или смещением контура всегда можно «вогнать» передачу в заданное межосевое расстояние.
Здравствуйте! В п.15, при расчете угла наклона,в формуле у Вас почему-то используется arcsin, по-моему должен быть arctg?
Почему, Сабир, Вы решили, что должен быть arctg?
Сам я эту формулу не выводил и не проверял, но в справочниках — arcsin. Например здесь: Справочник механика машиностроительного завода, том 1, стр.330.
ГОСТ 16532-70 Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет геометрии. См. формулу в пункте 8 на стр.6. Я подумал как то так должно быть. В любом случае по вашим формулам у меня что то не бьется))) там какая то запара с радианами
Сабир, вышлите через страницу «Обратная связь» или напишите здесь данные замеров ваших колеса и шестерни.
С радианами никакой «запары» нет. Погрешность многократных прямых и обратных тригонометрических вычислений, конечно, иногда проявляется в Excel.
С формулой не всё однозначно. В ГОСТе действительно arctg, в справочнике — arcsin. Ошибка может быть и там, и там. С arcsin я многократно успешно на практике использовал изложенный алгоритм. Конечно, при малых значениях угла arcsin (а)≈arctg (a), и в диапазоне углов наклона зубьев до 20° отличие arcsin от arctg не превышает 6%. На не особо точных передачах это различие можно и не заметить и не почувствовать.
Склоняюсь к тому, что Вы правы — должен быть arctg. Хочу проверить замерами и расчетами на реальном колесе, но в данный момент такой возможности нет, поэтому и прошу Вас прислать ваши данные.
Есть пара вопросов. Интересно Ваше мнение.
В предложенном расчете сначала считается
Δy через измеряемые величины da,df и коэф-ты ha*, c*,
а затем уже х, используя расчетный Δy и замеренный da.
Естественно, что нужно знать также d, для которого нужны m,z,угол B.
1. Задумываясь о максимальной точности расчета, вероятно, предпочтительнее было бы сразу посчитать х, измерив df и зная d, из формулы ГОСТа для расчета df:
df = d — 2*(ha*+c*-x) m, чтобы не вводить погрешность от измеренного da в расчет. Как вы считаете?
2. Хотя, даже для исходного контура крупномодульных колес, значение с* по ГОСТу может варьироваться в отдельных случаях, до 0.4, не говоря уже о мелкомодульных колесах, где при разном типе впадины может меняться с* и ha* — до 1,1.
Конечно, это все малая погрешность, но получается, что не зная межосевого расстояния (иногда такое встречалось) вычислить с абсолютной точностью х не получится.
Может, я и ошибаюсь. Что вы думаете?
df, как Вы справедливо отметили, величина для обратных пересчетов абсолютно не надежная. Поэтому я предпочел в первую очередь «посмотреть в расчете» на коэффициент уравнительного смещения.
Не зная межосевое расстояние очень сложно точно восстановить передачу с коррегированными профилями, практически невозможно.
Здравствуйте! А какой модуль зуба у шестерни с Да = 24, Дф = 15, кол-во зубов 8? 2.4 или 2.73?
Здравствуйте, Роман. Читайте статью и смотрите — какие исходные данные нужно знать.
Соответственно получается m1 = 24/(8+2) = 2.4, если замеры правильные. Но, если, исходя из формулы посчитать Дф, то получится, что он должен быть 13.2, а по замерам у меня получается 15! Не могу же я при замере ошибиться на 1.8мм.
Т.к. зубьев очень мало, то шестерня скорее всего выполнена со смещением исходного контура.
Для модулей стандартизованы ряды значений. m=2.4 — нет такого модуля!
Для точных правильных расчетов нужны параметры ответного колеса и межосевое расстояние передачи.
А так может быть много вариантов. Например: z1=8, m1=2.5, β=0, Δy=0.45, x1=0.25, d1=20, da1=24, df1=15.
Стартер для лодочного мотора.
Мне как раз нужно всё вычислить для того, чтобы сделать венец зубчатый на маховик двигателя. Единственное, что смогу точно сказать, но уже после 15 января 2022 года — это межосевое расстояние передачи.
Ну конечно же, эту шестерню могу всю измерить заново. Может быть фотки куда-нибудь можно отправить?
Давайте фото зуба с впадиной крупно — на a@al-vo.ru. Измерьте с точностью хотя бы ±0,05 мм толщину зуба на наружном диаметре, диаметр впадин, диаметр вершин, длину общей нормали, размер по роликам.
Фото сделайте по возможности ровно сверху, чтобы можно было попытаться сравнить с расчетными контурами наложением.
Полагаю с большой долей вероятности, что параметры вашей шестерни следующие: z1=8, m1=2.0, β1=0, x1=1.00, d1=16, da1=24, df1=15, W=10.448 (при zn=2), М=24.764 (при D=4,141).
Зубчатое колесо
Зубча́тое колесо́, шестерня́ — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса. В машиностроении принято малое зубчатое колесо с меньшим числом зубьев называть шестернёй, а большое — колесом. Однако часто все зубчатые колёса называют шестерня́ми.
Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования вращающего момента и числа оборотов валов на входе и выходе. Колесо, к которому вращающий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то вращающий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.
Содержание
Цилиндрические зубчатые колёса
Поперечный профиль зуба
Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако, существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
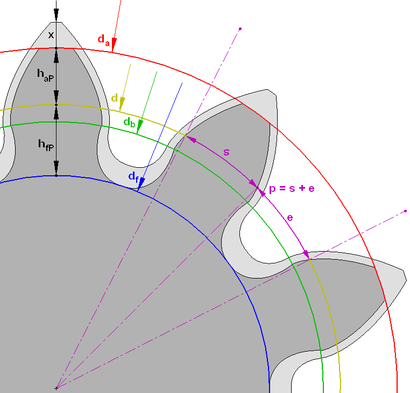
Параметры эвольвентного зубчатого колеса:
В машиностроении приняты определенные значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50.
Высота головки зуба — haP и высота ножки зуба — hfP — в случае т.н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: haP = m; hfP = 1,25 m, то есть:
Отсюда получаем, что высота зуба h (на рисунке не обозначена):
Вообще из рисунка ясно, что диаметр окружности вершин da больше диаметра окружности впадин df на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2: