Модуль комплексного числа что это

Модуль комплексного числа

Модуль комплексного числа

Модулем комплексного числа называется длина вектора, соответствующего этому числу: .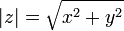
Модуль комплексного числа z обычно обозначается | z | или r.

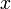
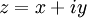
Пусть и — вещественные числа такие, что комплексное число (обычные обозначения). Тогда

Полезное

Смотреть что такое «Модуль комплексного числа» в других словарях:

модуль комплексного числа — kompleksinio skaičiaus modulis statusas T sritis fizika atitikmenys: angl. modulus of complex number vok. Betrag der komplexen Zahl, m rus. модуль комплексного числа, m pranc. module du nombre complexe, m … Fizikos terminų žodynas

МОДУЛЬ — (modulus) Величина числа с точки зрения его расстояния от 0. Модуль, или абсолютное значение реального числа х (обозначается |х|), является разностью между х и 0 независимо от знака. Следовательно, если х>0, то |х|=х и если х <0, то |х|=–х … Экономический словарь

МОДУЛЬ — комплексного числа см. Абсолютная величина. Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab … Большой Энциклопедический словарь

Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия

Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия

МОДУЛЬ — (в математике) мера для сравнения однородных величин и для выражения одной из них помощью другой; м. выражается числом. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. МОДУЛЬ (лат.). 1) число, которым множатся… … Словарь иностранных слов русского языка

МОДУЛЬ (в математике) — МОДУЛЬ комплексного числа, см. Абсолютная величина (см. АБСОЛЮТНАЯ ВЕЛИЧИНА). Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab … Энциклопедический словарь

Модуль — I Модуль (от лат. modulus мера) в архитектуре, условная единица, принимаемая для координации размеров частей здания или комплекса. В архитектуре разных народов в зависимости от особенностей строительной техники и композиции зданий за М.… … Большая советская энциклопедия

модуль — я; м. [от лат. modulus мера] 1. чего. Спец. Величина, характеризующая какое л. свойство твёрдого тела. М. сжатия. М. упругости. 2. Матем. Действительное число, абсолютная величина отрицательного или положительного числа. М. комплексного числа. М … Энциклопедический словарь

Источник

Модуль комплексного числа

Что такое комплексное число

Во множестве комплексных чисел содержится множество вещественных чисел. Если множество комплексных чисел — это всевозможные пары (x, y), то содержащееся в нем множество вещественных чисел — это пары (x, 0). Те же комплексные числа, которые задают пары (0, y) являются мнимыми.

Что такое модуль комплексного числа

Модуль комплексного числа — это длина вектора, который изображает комплексное число.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Любое комплексное число кроме 0 может быть выражено в тригонометрической форме.

В этом виде \(\left|z\right|\) — модуль комплексного числа z. Может обозначаться как p и r.

Если \(\left|z\right|\;=\;r,\) то r будет обозначать длину радиус-вектора точки M (x, y).

Вычисление модуля комплексного числа, если в алгебраической форме оно выглядит как z = x + iy, возможно по следующей формуле:

То есть модуль комплексного числа можно вычислить как квадратный корень из суммы квадратов действительной и мнимой его частей.

Модуль комплексного числа имеет следующие свойства:

Что такое аргумент комплексного числа

Аргумент комплексного числа — это угол \(\varphi\) радиус-вектора точки, соответствующей комплексному числу \(z\;:\;\varphi\;=\;arg\;z\) на комплексной плоскости. Этот угол измеряется в радианах.

Каждое комплексное число, которое не равно нулю, имеет бесконечное множество аргументов. Эти аргументы отличаются друг от друга на целое число полный оборотов — \(360^\circ\;\cdot\;k\) при k — любое число.

Связь аргумента комплексного числа с его координатами отражена в следующих формулах:

Важно помнить, что ни одна из этих формул отдельно недостаточна для того, чтобы найти аргументы. Формулы используются в совокупности, а также учитывается номер четвертый на координатной плоскости, в которой находится комплексное число.

Как вывести формулу модуля

Примеры решения задач

Задача

Найти модуль числа \(z\;=\;-5\;+\;15i\)

Решение

\(x\;=\;Re\;z\;=\;-15\) — действительная часть, а \(y\;=\;Im\;z\;=\;15\) — мнимая часть комплексного числа \(z\;=\;-5\;+\;15i.\)

Таким образом, модуль числа равен следующему выражению:

Задача

Найти расстояние между числами \(z_1\;=\;1\;-\;3i,\;z_2\;=\;-2\;+\;2i\) на комплексной плоскости.

Решение

Расстояние между двумя комплексными числами находятся как модуль разности комплексных чисел. Используем необходимую формулу:

Задача

Найти значение аргумента комплексного числа \(\sqrt<34>\) и выразить его в тригонометрической форме.

Решение

Теперь для нахождения тригонометрической формы записи комплексного числа необходимо найти модуль.

Исходя из этого, тригонометрическая форма комплексного числа выглядит следующим образом:

Задача

Решение

Источник

Комплексные числа

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Изображение

Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

Вычислить сумму и разность заданных комплексных чисел:

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:

Аналогично выполним вычитание чисел:

Выполнить умножение и деление комплексных чисел:

Так, теперь разделим первое число на второе:

Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:

Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:

Для возведения в квадрат достаточно умножить число само на себя:

Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:

В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.

Вычисляем значение модуля:

Найдем чем равен аргумент:

$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$

Записываем в тригонометрическом виде:

Преобразуем в алгебраическую форму для наглядности:

Представим число в тригонометрической форме. Найдем модуль и аргумент:

Используем знакомую формулу Муавра для вычисления корней любой степени:

Источник

Модуль числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Записывайся на занятия по математике для учеников с 1 по 11 классы.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

Оно равно a при а > 0 и −а, при а

Модуль комплексного числа

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Модуль вещественных чисел

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Закрепим свойства модуля числа, которые мы рассмотрели выше:

Источник

Комплексные числа

Известно, что квадратное уравнение с вещественными коэффициентами и отрицательным дискриминантом не имеет вещественных корней. В частности, уравнение
$$
z^2+1=0\nonumber
$$
не имеет корней на множестве \(\mathbb\). Возникает потребность расширить множество \(\mathbb\) так, чтобы на более широком множестве было разрешимо квадратное уравнение с любыми вещественными коэффициентами.

Определение комплексного числа.

Комплексными числами называют пары \((x,y)\) вещественных (действительных) чисел \(x\) и \(y\), для которых следующим образом определены понятие равенства и операции сложения и умножения.
Обозначим комплексное число \((x,y)\) буквой \(z\), то есть положим \(z=(x,y)\). Пусть \(z_1=(x_1,y_1)\), \(z_2=(x_2,y_2)\). Два комплексных числа \(z_1\) и \(z_2\) считаются равными тогда и только тогда, когда \(x_1=x_2\) и \(y_1=y_2\), то есть
$$
\<(x_1,y_1) = (x_2,y_2)\>\Leftrightarrow \\ \wedge\ \.\nonumber
$$

Сумма и произведение комплексных чисел \(z_1\) и \(z_2\) обозначаются соответственно \(z_1+z_2\) и \(z_1z_2\) и определяются формулами
$$
z_1+z_2=(x_1+x_2,y_1+y_2),\label
$$
$$
z_1z_2=(x_1x_2-y_1y_2,x_1y_2+x_2y_1).\label
$$

Из формул \eqref и \eqref следуют соотношения
$$
(x_1,0) + (x_2,0) = (x_1+x_2,0),\qquad (x_1,0)(x_2,0) = (x_1x_2,0),\nonumber
$$
которые показывают, что операции над комплексными числами вида \((x, 0)\) совпадают с операциями над действительными числами. Поэтому комплексное число вида \((x, 0)\) отождествляют с действительным числом \(x\), то есть полагают \((x,0) = x\).

Следовательно, любое комплексное число \(z= (x,y)\) можно записать в виде \(x + iy\), то есть
$$
z = x + iy.\label
$$

Запись комплексного числа \(z = (x,y)\) в виде \eqref называют алгебраической формой комплексного числа.

В записи \eqref число \(x\) называют действительной частью комплексного числа и обозначают \(Re\ z\), а число \(y\) — мнимой частью и обозначают \(Im\ z\), то есть
$$
Re\ z = x,\quad Im\ z = y. \nonumber
$$

Если \(x= 0\), то есть \(z = iy\), то такое комплексное число называют чисто мнимым.

Здесь и всюду в дальнейшем, если не оговорено противное, в записи \(x+iy\) числа \(x\) и \(y\) считаются действительными (вещественными).

Число \(\displaystyle\sqrt\) обозначают \(|z|\) и называют модулем комплексного числа \(z\), то есть
$$
|z|=|x + iy|=\sqrt.\label
$$
Заметим, что \(|z|\geq 0\) и \(\<|z| = 0\>\Leftrightarrow \\).

Комплексное число \(x-iy\) называют сопряженным комплексному числу \(z = x + iy\) и обозначают \(\overline\) то есть
$$
\overline = \overline= x-iy.\label
$$
Из равенств \eqref и \eqref следует, что
$$
|z| = |\overline|,\qquad z\overline=|z|^2,\label
$$
так как \(z\overline=(x+iy)(x-iy) = x^2 + y^2\).

Свойства операций.

Операции сложения и умножения комплексных чисел обладают свойствами:

Эти свойства вытекают из определения операций сложения и умножения комплексных чисел и свойств операций для вещественных чисел.

Из уравнения \eqref в силу правила равенства и определения суммы комплексных чисел следует, что
$$
z_1-z_2=(x_1-x_2)+i(y_1-y_2).\nonumber
$$

Деление на множестве \(\mathbb\) вводится как операция, обратная умножению, а частным от деления комплексного числа \(z_1=_1+iy_1\) на число \(z_2 = x_2 + iy_2\) называют такое число \(z\), которое удовлетворяет уравнению
$$
zz_2=z_1\label
$$
и обозначается \(z_1:z_2\) или \(\displaystyle \frac\).

Докажем, что уравнение \eqref для любых комплексных чисел \(z_1\) и \(z_2\), где \(z_2\neq 0\), имеет единственный корень.

\(\circ\) Умножая обе части уравнения \eqref на \(\overline_2\), получим в силу равенства \eqref уравнение
$$
z|z_2|^2 = z_1\overline_2,\label
$$
которое равносильно уравнению \eqref, так как \(\overline_2\neq 0\).

Эту формулу можно не запоминать — важно знать, что она получается умножением числителя и знаменателя на число, сопряженное со знаменателем.

Найти частное \(\displaystyle \frac\), если \(z_1=5-2i,\ z_2=3 + 4i\).

Источник