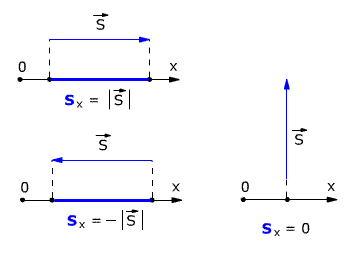
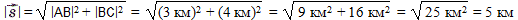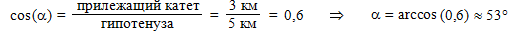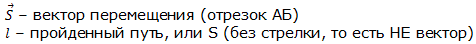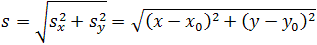Модуль перемещения что это
«Перемещение. Траектория. Путь» (9-й класс)
Разделы: Физика
Класс: 9
Демонстрации: Определение перемещения и пройденного пути.
1. Актуализация знаний.
– Здравствуйте, ребята! Садитесь! Сегодня мы с вами продолжим изучать тему “Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми понятиями (терминами), касающихся этой темы. А пока проверим выполнение вами домашнего задания у данному уроку.
2. Проверка домашнего задания.
Перед уроком один учащийся выписывает на доске решение следующего домашнего задания:
Двум учащимся раздаются карточки с индивидуальными заданиями, которые выполняются во время устной проверки упр. 1 стр. 9 учебника. [1]
1. Какую систему координат(одномерную, двухмерную, трехмерную) следует выбрать для определения положения тел:
а) трактор в поле;
б) вертолет в небе;
в) поезд
г) шахматная фигура на доске.
2. Дано выражение: S = υ0 · t + (а · t 2 ) / 2, выразите: а, υ0
1. Какую систему координат (одномерную, двухмерную, трехмерную) следует выбрать для определения положения таких тел:
а) люстра в комнате;
б) лифт;
в) подводная лодка;
г) самолет на взлетной полосе.
3. Изучение нового теоретического материала.
С изменениями координат тела связана величина, вводимая для описания движения, – ПЕРЕМЕЩЕНИЕ.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Перемещение принято обозначать буквой 
[ 
Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка, который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.

Знать вектор перемещения – значит, знать его направление и модуль. Модуль вектора – это скаляр, т.е. численное значение. Зная начальное положение и вектор перемещения тела, можно определить, где находится тело.
В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.
Воображаемая линия в пространстве, по которой движется тело называется ТРАЕКТОРИЕЙ движения тела.
Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Движение, при котором все точки тела движутся по одинаковым траекториям, называется поступательным.
Очень часто траектория – невидимая линия. Траектория движущейся точки может быть прямой или кривой линией. Соответственно форме траектории движение бывает прямолинейным и криволинейным.
Длина траектории – это ПУТЬ. Путь является скалярной величиной и обозначается буквой l. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.
Модуль перемещения и путь могут совпадать по значению, только в том случае, если тело движется вдоль прямой в одном направлении.
Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия: (Приложение 3) (раздаются в виде карточек каждому ученику)
| Путь | Перемещение | |
| Определение | Длина траектории, описываемой телом за определенное время | Вектор, соединяющий начальное положение тела с его последующим положением |
| Обозначение | l [ м ] | S [м ] |
| Характер физических величин | Скалярная, т.е. определяется только числовым значением | Векторная, т.е. определяется числовым значением (модулем) и направлением |
| Необходимость введения | Зная начальное положение тела и путь l, пройденный за промежуток времени t, нельзя определить положение тела в заданный момент времени t | Зная начальное положение тела и S за промежуток времени t, однозначно определяется положение тела в заданный момент времени t |
| l = S в случае прямолинейного движения без возвратов | ||
4. Демонстрация опыта (учащиеся выполняют самостоятельно на своих местах за партами, учитель вместе с учащимися выполняет демонстрацию этого опыта)
5. Упражнения и вопросы для повторения.
Повторение понятий урока:
– перемещение;
– траектория;
– путь.
7. Домашнее задание.
§ 2 учебника [1], вопросы после параграфа, упражнение 2 (стр.12) учебника [1], повторить выполнение опыта урока дома.
1. Перышкин А.В., Гутник Е.М. Физика. 9 кл.: учеб.для общеобразоват.учреждений – 9-е изд., стереотип. – М.: Дрофа, 2005.
Модуль перемещения что это
1.1 Механическое движение — это изменение положения тела в пространстве, относительно других тел с течением времени.
Различают три вида движения:
– поступательное — это движение, при котором все точки тела двигаются одинаково, то есть в одну и ту же сторону с одной и той же скоростью — тело движется как целое;
– вращательное — все точки тела движутся по окружностям;
– колебательное — это движение, которое повторяется (почти повторяется). Существенно отличие от вращательного движения — при колебаниях движение происходит во взаимно противоположных направлениях.
1.2 Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи; это тело, двигающееся поступательно (то есть любое тело при поступательном движении является материальной точкой).
1.3 Основная задача механики — определение положения движущегося тела в любой момент времени. За движением тела удобнее всего следить, отслеживая изменение его координат с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерить время, необходимы часы. Все это вместе образуют систему отсчета.
1.4 Система отсчета: тело отсчета (абсолютно любое тело, относительно которого наблюдается движение), жестко связанная с этим телом система координат и часы.
1.5 При движении тело движется вдоль некоторой линии, называемой траекторией. В зависимости от выбранной системы отсчета траектория может выглядеть по-разному.
1.6 Путь (S, [S] = м/с) — это длина участка траектории, пройденного за данный промежуток времени.
1.7 Перемещение — это вектор, соединяющий начальное положение тела с конечным.
В процессе движения путь может только увеличиваться, а перемещение и увеличиваться и уменьшаться. При прямолинейном движении в одном направлении путь равен модулю перемещения, в любом другом случае, когда тело движется по произвольной траектории — путь больше модуля перемещения (см. рис.). Самое главное: путь — величина скалярная; перемещение — величина векторная.
1.8 Модуль перемещения — это длина вектора перемещения. Если нам известны проекции перемещения на оси координат
и
то модуль перемещения всегда можно найти по теореме Пифагора:
1.9 Радиус-вектор — вектор, начало которого совпадает с началом координат, а конец с положением тела в данный момент времени. Радиус-вектор позволяет задать положение точки в пространстве.
Проекции радиус-вектора на оси координат являются координатами тела в данный момент времени. Перемещение тела можно выразить, зная радиус-вектор в начальный и конечный моменты времени (см. рис.):
1.10 Закон движения — это закон, по которому радиус-вектор меняется со временем. Задача механики — определить координаты тела в любой момент времени, т. е. установить функцию
Кинематика. Перемещение и путь.
Перемещением в механике называют вектор (направленный отрезок прямой), соединяющий начальное и последующее положения тела.
Понятие вектора перемещения вводится для решения задачи кинематики – определить положение тела в пространстве в данный момент времени, если известно его начальное положение.
Допустим, точка М движется по криволинейной траектории и в некоторые моменты времени t1 и t2 оказывается в точках М1 и М2 соответственно. Вектор 


Путь – это длина участка траектории, пройденного телом за данный промежуток времени. В общем случае модуль вектора перемещения не равен длине пути, пройденного телом за некоторый промежуток времени, поскольку траектория может быть криволинейной, а тело может менять направление движения.
Модуль вектора перемещения и путь могут быть равны только при прямолинейном движении в одном направлении. При изменении направления прямолинейного движения модуль вектора перемещения будет меньше пути.
При криволинейном движении модуль вектора перемещения тоже меньше пути, поскольку хорда всегда меньше дуги, которую она стягивает.
Путь и перемещение тела
С понятием пути вы уже неоднократно сталкивались. Познакомимся теперь с новым для вас понятием – перемещением, которое более информативно и полезно в физике, чем понятие пути.
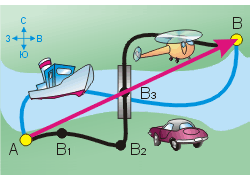
Допустим, из пункта А в пункт В на другом берегу реки нужно переправить груз. Это можно сделать на автомобиле через мост, на катере по реке или на вертолёте. В каждом из этих случаев путь, пройденный грузом, будет разным, но перемещение будет неизменным: из точки А в точку В.
Перемещением называют вектор, проведённый из начального положения тела в его конечное положение. Вектор перемещения показывает расстояние, на которое переместилось тело, и направление перемещения. Обратите внимание, что направление перемещения и направление движения – два разных понятия. Поясним это.
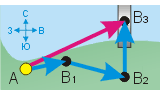
Рассмотрим, например, траекторию движения автомобиля от пункта А до середины моста. Обозначим промежуточные точки – В1, В2, В3 (см. рисунок). Вы видите, что на отрезке АВ1 автомобиль ехал на северо-восток (первая синяя стрелка), на отрезке В1В2 – на юго-восток (вторая синяя стрелка), а на отрезке В2В3 – на север (третья синяя стрелка). Итак, в момент проезда моста (точки В3) направление движения характеризовалось синим вектором В2В3, а направление перемещения – красным вектором АВ3.
Итак, перемещение тела – векторная величина, то есть имеющая пространственное направление и числовое значение (модуль). В отличие от перемещения, путь – скалярная величина, то есть имеющая только числовое значение (и не имеющая пространственного направления). Путь обозначают символом l, перемещение обозначают символом 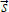
Почему в физике не ограничились понятием пути, а ввели более сложное (векторное) понятие перемещения? Зная модуль и направление перемещения, всегда можно сказать, где будет находиться тело (по отношению к своему начальному положению). Зная путь, положение тела определить нельзя. Например, зная лишь, что турист прошёл путь 7 км, мы ничего не можем сказать о том, где он сейчас находится.
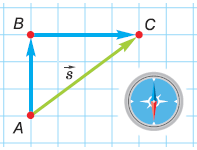
Задача. В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.
Решение 1 – с измерениями линейкой и транспортиром.
Перемещение – это вектор, соединяющий начальное и конечное положения тела. Начертим его на клетчатой бумаге в масштабе: 1 км – 1 см (чертёж справа). Измерив линейкой модуль построенного вектора, получим: 5 см. Согласно выбранному нами масштабу, модуль перемещения туриста равен 5 км. Но напомним: знать вектор – значит знать его модуль и направление. Поэтому, применив транспортир, определим: направление перемещения туриста составляет 53° с направлением на север (проверьте сами).
Решение 2 – без использования линейки и транспортира.
Поскольку угол между перемещениями туриста на север и на восток составляет 90°, применим теорему Пифагора и найдём длину гипотенузы, так как она одновременно является и модулем перемещения туриста:
Как видите, это значение совпадает с полученным в первом решении. Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):
Итак, задача решена двумя способами с совпадающими ответами.
Траектория
Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
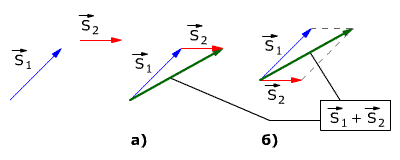
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 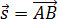
Выберем ось ОХ так, чтобы вектор 
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть
Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
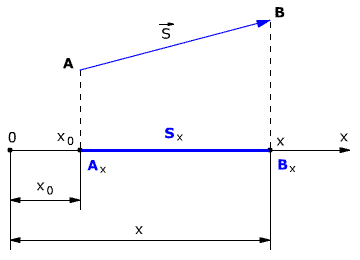
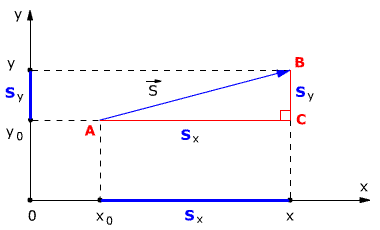
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
По теореме Пифагора
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.