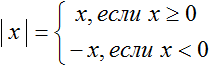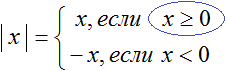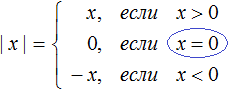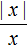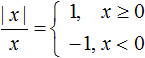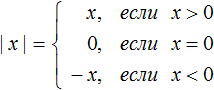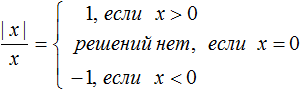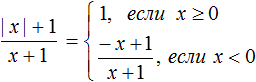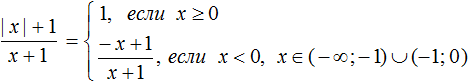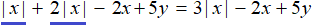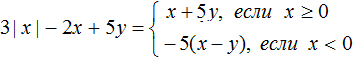Модуль в геометрии что это

Модули. Применение геометрического смысла модуля при решений уравнений и неравенств

Цель: Актуализировать знания школьников о смысле понятия «модуль». Учить их применять эти знания при решении уравнении, неравенств и систем уравнении с модулями.

Для того, чтобы научиться решать уравнения и неравенства с модулем, необходимо хорошо разобраться с понятием модуля, его геометрическим смыслом и свойствами.

С рассмотрения этого материала мы и начнем наше занятие.

1. Определение: Модулем числа называется само число, если оно неотрицательно, или число противоположное данному, если оно отрицательно.

Следовательно, при любых значениях переменной |а| есть число неотрицательное.

2. Рассмотрим основные свойства модуля, которые используются при решении уравнений и неравенств, содержащих модуль.

Свойства модуля

— Модуль числа есть величина неотрицательная: |а|>0 или равно 0.

— Модули противоположенных чисел равны: |а|= |-а|

— Модуль произведения равен произведению модулей множителей: |а*в|= |а|*|в|.

— Модуль частного равен частному модулей числителя и знаменателя: |а/в|=|а|/|в|, где в не равен нулю.

— Модуль суммы не больше суммы модулей ее слагаемых: |а+в|≤|а|+|в|.

При этом равенство |а+в|=|а|+|в| имеет место тогда и только тогда, когда слагаемые одного знака или одно из слагаемых равно нулю.

— Два числа, модули которых равны, либо равны между собой, либо отличаются только знаками, то есть являются противоположными: |а|=|в|, если, а=в или, а=–в.

Преобразование выражений, содержащих модули

При решении уравнении и неравенств с модулем, часто приходится преобразовывать их, раскрывая знак модуля.

Рассмотрим, по каким правилам раскрывается модуль.

Из определения модуля следует: чтобы раскрыть знак модуля, надо знать знак подмодульного выражения.

Составим схему раскрытия модуля:

а) если знак подмодульного выражения неотрицателен, то знак модуля опускается: |а| =а.

б) если знак подмодульного выражения отрицателен, то подмодульное выражение умножается на (-1), то есть заменяется противоположенным выражением: |а| =-1а.

Рассмотрим несколько примеров.

Пример 1.1

б) |3+х|, если х 5, то х-2 > 0, поэтому |х-2|=х-2;

4. Задания для самостоятельной работы

б) |- 3/7х|, если х 2 |, если а > 0;

3. Решить неравенство самостоятельно:

4. Решить уравнение:

5. Решить уравнение:

6. Решить неравенство:

7. Найдите наибольшее натуральное значение параметра с при котором решение неравенства

Это задание можно предложить сильным школьникам для домашней работы с последующей проверкой на уроке.

2. Для решения неравенства сделаем ещё два рисунка.

Значение выражения, стоящего под модулем, не должно превышать 2, значит

Значение выражения, стоящего под модулем, должно быть больше, чем 48 единиц, значит:

Источник

Что такое модуль числа в математике

Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.

Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.

Графически абсолютное значение а обозначается как |a|.

Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.

Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.

Геометрическое значение

Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.

Графически это можно выразить следующим образом: |a| = OA.

Свойства абсолютной величины

Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:

Особенности решения уравнений с модулем

Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.

К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.

|А + 5| = А + 5, если, А больше или равняется нулю.

5-А, если, А значение меньше нуля.

В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.

Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.

Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.

Источник

Модуль числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Записывайся на занятия по математике для учеников с 1 по 11 классы.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

Оно равно a при а > 0 и −а, при а

Модуль комплексного числа

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Модуль вещественных чисел

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Закрепим свойства модуля числа, которые мы рассмотрели выше:

Источник

Обобщённое понятие модуля числа

В данном уроке мы рассмотрим понятие модуля числа более подробно.

Что такое модуль?

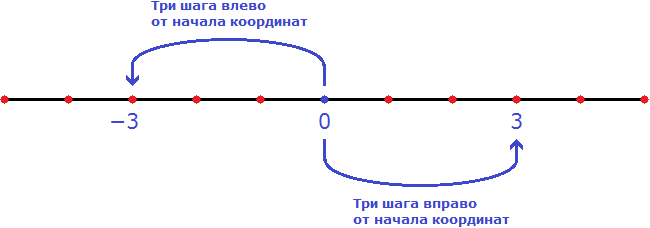
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3

Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:

Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:

Где x₁ и x₂ — числа на координатной прямой.

Например, отметим на координатной прямой числа 2 и 5.

Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:

Видим, что расстояние от числа 2 до числа 5 равно трём шагам:

Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3

То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:

Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:

Это равенство можно прочитать так: Расстояние от x₁ до x₂ равно расстоянию от x₂ до x₁.

Раскрытие модуля

Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.

Правило раскрытия модуля выглядит так:

В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.

Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x

Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5

В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0

Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.

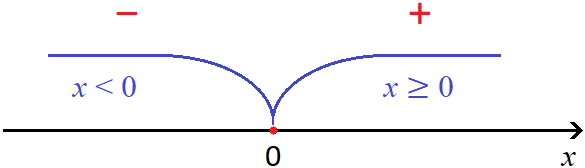
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:

А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:

Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,

Корень из числа 4 равен 2. Тогда модуль примет вид

x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x |√4 − 6| = |2 − 6| = |−4| = −(−4) = 4

На практике обычно рассуждают так:

«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».

Примеры:

|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0

Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:

В данном случае выполняется условие x=0, ведь 0 = 0

Пример 5. Раскрыть модуль в выражении |x|+ 3

Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.

Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:

Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 |x| + 3 = 3 − x = 3 − (−6) = 9

Пример 6. Раскрыть модуль в выражении x +|x + 3|

Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11

Найдём значение выражения x +|x + 3| при x=−3.

Пример 3. Раскрыть модуль в выражении

Как и прежде используем правило раскрытия модуля:

В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0

Перепишем решение так:

Пример 4. Раскрыть модуль в выражении

Но надо учитывать, что при x = − 1 знаменатель выражения 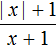обращается в ноль. Поэтому второе условие x следует дополнить записью о том, какие значения может принимать x

Преобразование выражений с модулями

Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.

Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.

Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.

Решение

Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:

В итоге имеем следующее решение:

Пример 2. Раскрыть модуль в выражении: −|x|

Решение

Источник

Что такое модуль действительного числа

В данной публикации мы рассмотрим определение, геометрическую интерпретацию, график функции и примеры модуля положительного/отрицательного числа и нуля.

Определение модуля числа

Модуль действительного числа (иногда называется абсолютной величиной) – это величина, равная ему же, если число положительное или равная противоположному, если оно отрицательное.

Модуль числа a обозначается вертикальными черточками с обеих сторон от него – |a|.

Противоположное число отличается от исходного знаком. Например, для числа 5 противоположным является -5. При этом ноль является противоположным самому себе, т.е.

Геометрическая интерпретация модуля

Модуль числа a – это расстояние от начала координат (O) до точки A на координатной оси, которая соответствует числу a, т.е.

График функции с модулем

График четной функции y = |х| выглядит следующим образом:

Чему равняются следующие модули |3|, |-7|, |12,4| и |-0,87|.

Решение:
Согласно приведенному выше определению:

Источник