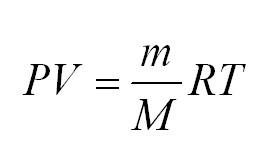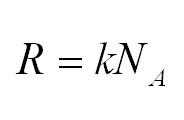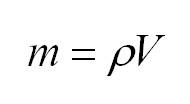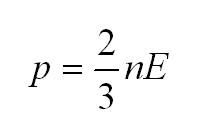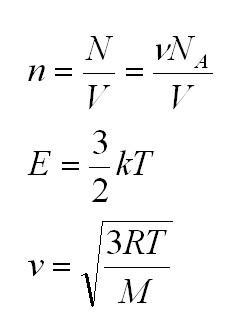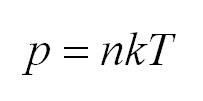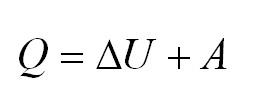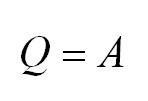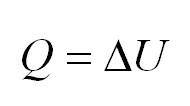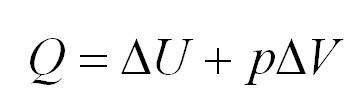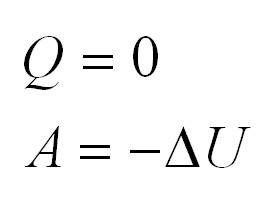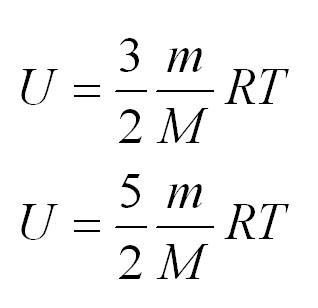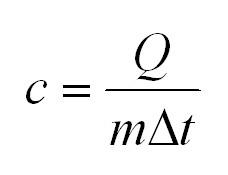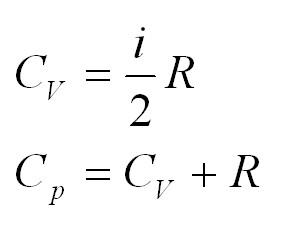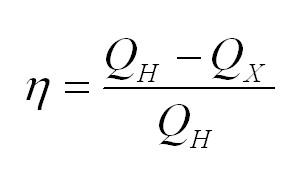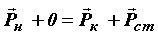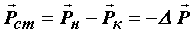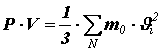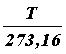Молекулярная математика что такое

Массовая доля

Что такое массовая доля

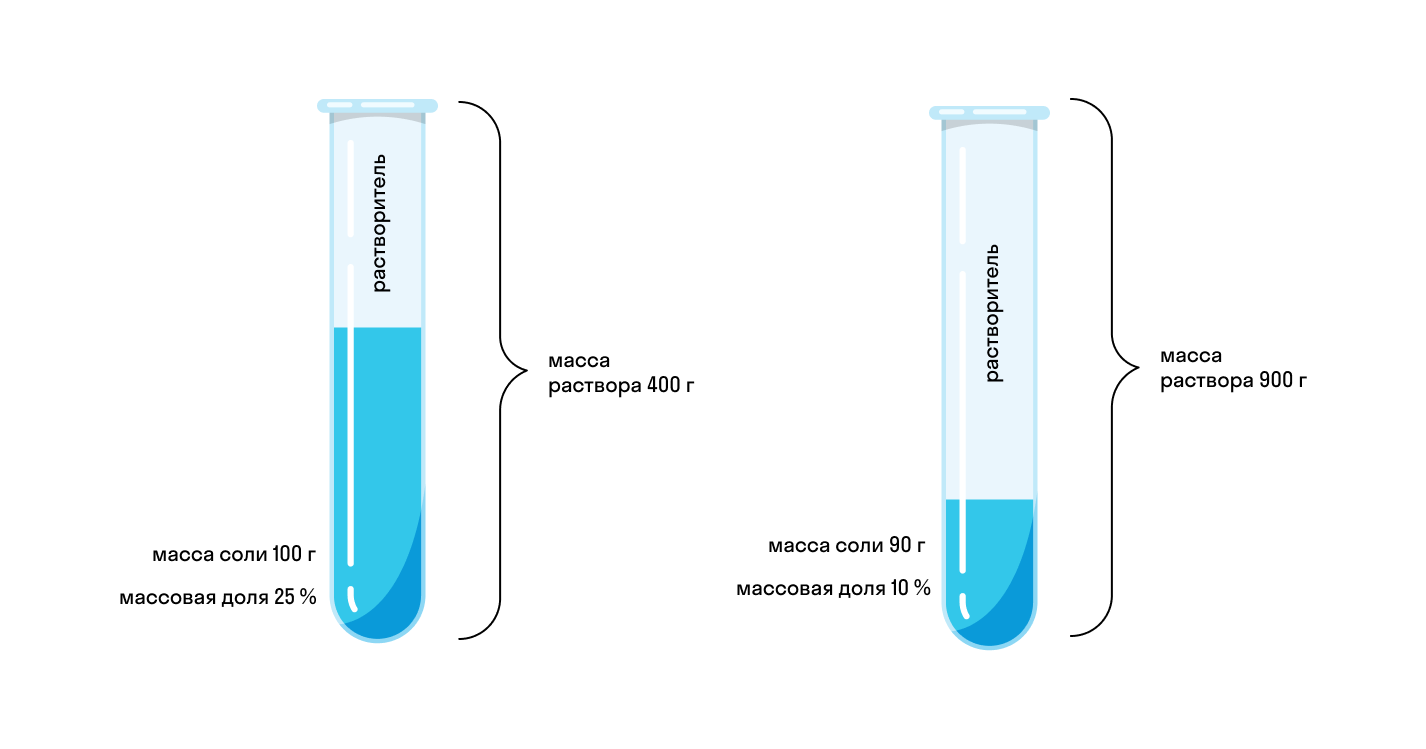
Начнем с примера: допустим, мы приготовили два раствора соли. Первый имеет массу 400 г и для него использовано 100 г соли. Масса второго 900 г и для него использовали 90 г соли. Какой раствор будет более концентрированным? Чтобы это понять, нужно выяснить процент соли в каждом растворе. Можно сказать иначе — нужно определить, какую долю в растворе занимает соль.

Массовая доля — это отношение растворенного вещества к массе раствора. Она может измеряться в процентах (от 0 до 100%) или в долях от единицы (от 0 до 1).

Как найти массовую долю растворенного вещества, расскажет формула:

где — обозначение массовой доли;

В нашем примере и без формул понятно, что в первом растворе соль занимает 25%, а в то втором — только 10%. А что будет, если в первый раствор добавить еще столько же соли и воды? Очевидно, что на концентрацию это не повлияет. Доля соли останется прежней, пусть даже масса раствора увеличилась.

Массовая доля химического элемента — это отношение между относительной массой его атомов и относительной молекулярной массой соединения, частью которого является данный элемент.

Как видите, фактическая масса сложного вещества или его отдельного компонента не имеет значения. Если мы не знаем этих показателей, для расчетов берутся относительные величины.

Такое определение массовой доли элемента выражается формулой:

— количество атомов искомого элемента;

— относительная атомная масса элемента;

— относительная молекулярная масса сложного вещества.

Если нужен показатель в процентах, результат надо умножить на 100%.

Относительная атомная и молекулярная масса

В формуле нахождения массовой доли мы видим две важные составляющие: относительную массу атома элемента (A_r) и относительную массу молекулы вещества (M_r). Разберемся, что это такое. И та, и другая величина — это отношение реальной массы к эталонной единице, за которую взята 1/12 массы атома углерода.

Относительная атомная масса элемента (A_r) говорит о том, насколько масса его атома больше 1/12 массы атома углерода. Для каждого элемента эта величина является постоянной и ее можно увидеть в таблице Менделеева.

Относительная молекулярная масса соединения (M_r) складывается из относительных атомных масс всех элементов в составе его молекулы. Она показывает, насколько молекула вещества больше 1/12 массы атома углерода.

Это не измеряемые величины, то есть они не имеют единиц измерения. Буква r в обозначениях относительной атомной и молекулярной массы восходит к английскому слову relative — «относительный».

Как найти массовую долю элемента в веществе

Выше мы рассмотрели формулу для вычисления массовой доли химического элемента в веществе и узнали, откуда берутся ее составляющие. Применим эти знания на практике.

Пример 1

Оксид магния массой 8 г образовался при вступлении 4,8 г магния в реакцию с кислородом. Каковы массовые доли магния и кислорода в полученном оксиде?

Решение:

Для начала вычислим массу кислорода. Согласно закону сохранения массы веществ в соединении можно воспользоваться формулой m(O) = m(MgO) − m(Mg).

Вспоминаем, как найти массовую долю элемента в веществе: нужно понять, какую часть соединения оно составляет.

Зная массы каждого компонента оксида, сделать расчет несложно:

Ответ: массовые доли магния и кислорода в оксиде магния составляют 60% и 40% соответственно.

Пример 2

Потренируемся находить массовую долю элемента в сложном веществе. Определим, какую часть этилового спирта С₂H₆O составляет водород.

Решение:

В данном случае у нас нет конкретных указаний на массы элементов или всего вещества. Но мы можем воспользоваться другой формулой массовой доли в химии, которая позволяет работать с относительными величинами:

Согласно таблице Менделеева относительная атомная масса водорода равна единице.

Вычислим относительную молекулярную массу соединения С₂H₆O, которая складывается из соответствующих масс каждого элемента:

Mr(С₂H₆O) = 2M(C) + 6M(H) + M(O) = 212 + 6 1 + 16 = 46.

Полученные данные подставим в формулу и определим массовую долю элемента в соединении:

Ответ: в этиловом спирте массовая доля водорода составляет 13%.

Как вычислить массовую долю вещества в растворе

Вспомним, что такое концентрация раствора. Она говорит о том, в каком соотношении находятся растворенное вещество и растворитель, а другими словами — сколько растворенного вещества содержится в единице объема или массы. Концентрация может быть безразмерной величиной и выражаться в процентах, но также ее можно выразить в массовых или в молярных долях.

В случае с растворами применима та же формула:

Если нужно значение в процентах, результат надо умножить на 100%.

Пример

Требуется приготовить 0,5 л раствора карбоната натрия плотностью 1,13 г/мл. Определите массу карбоната натрия при условии, что концентрация раствора должна быть 13%.

Решение:

Вначале нам нужно узнать массу раствора, что легко сделать, когда известны его объем и плотность. Воспользуется формулой m(р–ра) = ρ × V

m(р–ра) = 500 × 1,13 = 565 г.

Дальше вспомним, как находить массовую долю растворенного вещества:

Поскольку концентрация раствора — это и есть массовая доля растворенного вещества, подставим ее в уравнение:

m(Э) = 0,13 × 565 = 73,45 г.

Ответ: для раствора понадобится 73,45 г карбоната натрия.

Вопросы для самопроверки:

Как обозначается массовая доля и в чем она выражается?

В чем разница между молекулярной массой вещества и его молярной массой?

Как найти массовую долю элемента в веществе, если мы знаем массу элемента и массу вещества?

Как рассчитать массовую долю вещества в растворе?

В каких безразмерных и размерных величинах можно выразить концентрацию раствора?

Источник

Основные формулы термодинамики и молекулярной физики, которые вам пригодятся

Основные формулы термодинамики и молекулярной физики, которые вам пригодятся. Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

Основное уравнение молекулярно-кинетической теории (МКТ)

Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:

Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:

Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ

Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:

Внутренняя энергия одноатомного и двухатомного идеального газа

Теплоемкость

Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.

Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Молекулярно-кинетическая теория

Экзаменационный проект за курс полной средней школы по предмету «Физика»

Автор: учащийся 11 «А» класса Болтунов Артем

г. Реутов Московской области 2008 год

Основные положения теории

Изображение атомов на поверхности кремния, полученное с помощью туннельного микроскопа.

Начиная с XVIII века, постепенно стала складываться система научных представлений о строении вещества, позднее названная молекулярно-кинетической теорией (МКТ). Молекулярно-кинетическая теория базируется на трёх положениях, обобщающих результаты большого количества экспериментальных данных:

Все тела состоят из мельчайших частиц – атомов, молекул и ионов. Таким образом любое вещество обладает дискретной структурой.

Частицы, образующие вещество, находятся в непрерывном хаотическом движении, которое называется тепловым.

Атомы, молекулы и ионы взаимодействуют друг с другом.

Рассмотрим эти положения несколько подробней.

Молекулярное строение вещества.

Число Авогадро. Количество вещества.

Современная физика не устанавливает пределы структурной делимости материи, однако, однозначно утверждает, что элементами, определяющими основные физические свойства тел, являются атомы, молекулы и ионы.

Атомом называется наименьшая частица данного химического элемента, являющаяся носителем его свойств.

Каждому химическому элементу соответствует свой атом.

Молекула – это устойчивая наименьшая частица данного вещества, обладающая его основными химическими свойствами.

Молекула состоит из атомов одинаковых или различных химических элементов.

Ион – электрически заряженная частица, которая образуется при потере или приобретении атомами и молекулами одного или нескольких электронов.

Атомное строение имеют инертные газы (гелий, аргон и др.), жидкости (ртуть) и твердые тела (медь, алмаз). Ряд кристаллических веществ, например, хлористый натрий, состоит из разноимённо заряженных ионов. Однако подавляющее большинство веществ образовано из молекул (углекислый газ, вода), поэтому понятие “молекула” часто используется как общий собирательный термин.

Естественно, что при таких размерах масса атомов и молекул также очень мала, к примеру, масса молекулы водорода составляет 3.3·10–27 кг. Понятно, что оперировать такими величинами в практических расчетах не совсем удобно.

Поэтому было введено понятие относительной молекулярной (атомной) массы Mr, которое определяется как отношение массы молекулы (атома) данного вещества m0 к 1/12 массы атома углерода:

. (1)

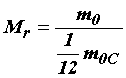
Число молекул в случае однокомпонентной системы, содержащей молекулы или атомы одного вида, можно найти по формуле:

,

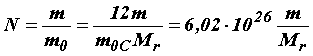
где m – масса системы, выраженная в килограммах.

Из этой формулы видно, что N имеет очень большие значения, поэтому потребовалось введение некоторого относительного параметра, связанного с числом молекул N в системе, называемого количеством вещества.

В Международной системе единиц (СИ) в качестве такого параметра принят моль – количество вещества, в котором содержится столько же молекул или атомов, сколько атомов содержится в 0.012 кг углерода.

Таким образом, в одном моле любого вещества содержится одно и тоже число молекул или атомов, которое называется числом (постоянной) Авогадро и равно:

.

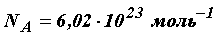
Количество вещества  определяется как число молей, равное отношению числа молекул N к числу Авогадро:

. (2)

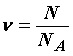
Масса одного моля вещества называется молярной массой. Она равна произведению массы одной молекулы вещества m0 на число Авогадро:

и измеряется в килограммах на моль: [M] = кг·моль–1.

Из (1), (3) и определения числа Авогадро следует, что между относительной молекулярной массой вещества Mr и его молярной массой M существует соотношение:

где m – масса вещества,

по формулам (2) и (3) легко получить ещё одно выражение для количества вещества:

, (4)

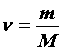
т. е. количество вещества равно отношению массы этого вещества к его молярной массе.

Тепловое движение молекул.

В результате взаимной диффузии веществ происходит постепенное выравнивание их концентрации во всех областях занимаемого ими объёма.

Установлено, что скорость протекания процесса диффузии зависит от рода диффундирующих веществ и температуры. Одним из наиболее интересных явлений, подтверждающих хаотичность движения молекул, является броуновское движение. Оно представляет собой тепловое движение микроскопических (но состоящих из очень большого числа молекул) частиц вещества, находящихся во взвешенном состоянии в жидкости или в газе, впервые наблюдаемое Р. Броуном. Беспорядочность перемещения таких частиц объясняется тем, что сумма импульсов, полученных ими от молекул с разных сторон, может стать не равной нулю как вследствие разного числа ударов с разных сторон частицы, так и в результате того, что частицу с одной стороны могли ударить молекулы, обладающие большими скоростями, чем молекулы, ударившие ее с другой стороны.

Броуновское движение проявляется тем заметнее, чем меньше частицы и вязкость среды, и чем выше температура системы. Зависимость от температуры свидетельствует о том, что скорость хаотического движения молекул возрастает с увеличением температуры, именно поэтому его и называют тепловым движением.

Сила притяжения уменьшается с увеличением r намного медленнее силы отталкивания, поэтому существует некоторое значение межмолекулярного расстояния r = r0, на котором силы отталкивания и притяжения компенсируют друг друга, так что результирующая сила межмолекулярного взаимодействия обращается в нуль.

Изменение агрегатного состояния вещества

Всякое вещество может находиться в трёх агрегатных состояниях: в твёрдом, жидком и газообразном.

В жидкости средняя энергия взаимодействия молекул примерно равна средней энергии теплового движения. Тепловое движение нарушает связь между молекулами и приводит к перемещению их относительно друг друга внутри объёма жидкости. В связи с этим жидкость принимает форму сосуда, в который она помещена.

Под твердыми телами обычно подразумеваются кристаллы, характерной особенностью которых является регулярное расположение в них атомов или ионов. О совокупности точек, в которых расположены атомные ядра, говорят как о кристаллической решетке, а сами эти точки называют узлами решетки.

Тепловое движение атомов или ионов кристалла носит в основном колебательный характер. Однако, поскольку в кристалле кинетическая энергия колебательного движения атомов значительно меньше абсолютного значения потенциальной энергии их взаимодействия, то тепловое движение не может разрушить связь между атомами. Поэтому твердое тело, в отличие от жидкости, сохраняет свою форму и обладает большой механической прочностью.

Кроме кристаллических тел существуют аморфные тела. Они, хотя и рассматриваются обычно как твердые, представляют собой переохлажденные жидкости. Если рассматривать некоторый атом аморфного тела как центральный, то ближайшие к нему атомы будут располагаться в определенном порядке, но по мере удаления от «центрального» атома этот порядок нарушается и расположение атомов становится случайным. К аморфным телам относятся стекло, пластмассы и т.д.

Переход из одного агрегатного состояния в другое (при постоянном давлении) происходит при строго определённой температуре и всегда связан с выделением или поглощением некоторого количества тепла. Переход вещества из одного состояния в другое происходит не мгновенно, а в течении некоторого времени, когда два состояния вещества существуют одновременно в тепловом равновесии.

Плавление и кристаллизация

По мере возрастания температуры энергия колебательного движения атомов в твёрдом теле возрастает и, наконец, наступает такой момент, когда связи между атомами начинают разрываться. При этом твердое тело переходит в жидкое состояние. Такой переход называется плавлением. При фиксированном давлении плавление происходит при строго определённой температуре.

Количество тепла, необходимое для превращения единицы массы вещества в жидкость при температуре плавления, называют удельной теплотой плавления .

Для плавления вещества массой m необходимо затратить количество теплоты равное:

При охлаждении расплавленного твёрдого тела происходит обратный процесс, называемый кристаллизацией. Образование кристалла также происходит при постоянной температуре, равной температуре плавления. При кристаллизации жидкости выделяется такое же количество теплоты, какое поглощается при плавлении вещества той же массы.

Аморфные тела в противоположность кристаллам не имеют определенной температуры плавления.

Испарение и конденсация.

Количество тепла Q, которое необходимо сообщить жидкости для испарения единицы её массы при постоянной температуре, называется удельной теплотой парообразования r.

Количество теплоты, которое надо затратить, чтобы перевести в пар жидкость массой m,

В результате хаотического движения над поверхностью жидкости молекула пара, попадая в сферу действия молекулярных сил, вновь возвращается в жидкость. Этот процесс называется конденсацией. Испарение жидкости происходит при любой температуре и тем быстрее, чем выше температура, больше площадь свободной поверхности испаряющейся жидкости и быстрее удаляются образовавшиеся над жидкостью пары.

Насыщенные и ненасыщенные пары. Влажность.

Пар, плотность которого меньше плотности насыщающего пара при той же температуре, называют ненасыщающим (или ненасыщенным).

Ненасыщенный пар подчиняется законам идеального газа.

Частным случаем испарения является кипение. Это процесс интенсивного парообразования не только со свободной поверхности, но и в объеме жидкости. В объеме образуются пузыри, заполненные насыщенным паром. Они поднимаются вверх под действием выталкивающей силы и разрываются на поверхности. Центрами их образования являются мельчайшие пузырьки посторонних газов или частиц различных примесей.

Процесс превращения жидкости в пар требует затрат энергии на разрыв связей между молекулами жидкости и на работу против сил внешнего давления. Давление насыщенного пара Pнас внутри пузырька, находящегося у поверхности жидкости, равно сумме внешнего давления на жидкость Рвн и давления под искривленной поверхностью жидкости.

Плотность насыщенного водяного пара при данной температуре есть величина табличная. Для определения относительной влажности надо знать абсолютную влажность, которую можно определить по точке росы.

Точке росы соответствует температура, при которой пар, находящийся в воздухе, становится насыщающим.

Молекулярно-кинетическая теория идеальных газов

Температура. Шкала температур Цельсия.

Молекулярная физика и термодинамика изучают свойства и поведение макроскопических систем, т.е. систем, состоящих из огромного числа атомов и молекул. Типичные системы, с которыми мы сталкиваемся в повседневной жизни, содержат около 1025 атомов.

При исследовании таких систем важнейшими являются макроскопические величины, непосредственно измеряемые опытным путём и характеризующие свойства всей совокупности молекул в целом. Учитывая необычайную сложность макросистем, следует начать изучение с наиболее простых объектов – систем, состояние которых не меняется со временем. Состояние макроскопической системы, в котором она может находится неопределённо долгое время, называется равновесным (о нём говорят также, как о состоянии теплового равновесия).

Равновесное состояние системы в целом может быть описано при помощи величин, называемых макроскопическими параметрами, к числу которых относят давление, объем и т. д. Каждый из параметров характеризует некоторое свойство системы. Так объем V мера свойства системы занимать ту или иную область пространства; давление Р – мера свойства системы сопротивляться внешнему изменению ее объёма.

В состоянии теплового равновесия макроскопические параметры не меняются со временем, остаются постоянным.

Одним из наиболее важных параметров, характеризующих равновесные свойства макроскопической системы, является температура. Введем этот параметр, для чего рассмотрим два тела, которые могут взаимодействовать и обмениваться энергией. Этот тип взаимодействия, который называется тепловым, приводит к тому, что в результате столкновений молекул в области контакта двух тел происходит передача энергии от быстрых молекул к медленным. Это означает, что энергия движения атомов в одном теле уменьшается, в другом – увеличивается. Тело, которое теряет энергию, называют более нагретым, а тело, к которому энергия переходит – менее нагретым. Такой переход энергии продолжается до тех пор, пока не установится состояние теплового равновесия. В состоянии теплового равновесия степени нагретости тел одинаковы. Для характеристики степени нагретости тела вводят параметр, называемый температурой.

Из опыта известно, что при изменении температуры изменяются размеры тел, электрическое сопротивление и другие свойства. Таким образом, температуру можно определить по изменению какого-либо удобного для измерения физического свойства данного вещества.

Чаще всего для измерения температур используют свойство жидкости изменять объем при нагревании и охлаждении. Прибор, с помощью которого измеряется температура, называется термометром.

Обыкновенный жидкостной термометр состоит из небольшого стеклянного резервуара, к которому присоединена стеклянная трубка с узким внутренним каналом. Резервуар и часть трубки наполнены ртутью или другой жидкостью. Температуру среды, в которую погружен термометр, определяют по положению верхнего уровня ртути в трубке. Деления на шкале условились наносить следующим образом. Цифру 0 ставят в том месте шкалы, где устанавливается уровень столбика жидкости, когда термометр опущен в тающий снег, цифру 100 – в том месте, где устанавливается уровень столбика жидкости, когда термометр погружен в пары воды, кипящей при нормальном давлении (105 Па). Расстояние между этими метками делят на 100 равных частей, называемых градусами. Такая температурная шкала создана Цельсием. Градус по шкале Цельсия обозначают °С.

Кроме макроскопических параметров вводят параметры системы, связанные с индивидуальными характеристиками составляющих её частиц, называемые микроскопическими. К их числу относятся в первую очередь масса частиц, их скорость, кинетическая энергия.

Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа.

Теория создана немецким физиком Р. Клаузисом в 1957 году для модели реального газа, которая называется идеальный газ. Основные признаки модели:

расстояния между молекулами велики по сравнению с их размерами;

взаимодействие между молекулами на расстоянии отсутствует;

при столкновениях молекул действуют большие силы отталкивания;

время столкновения много меньше времени свободного движения между столкновениями.

Молекулярно-кинетическая теория (МКТ) устанавливает связи между макро- и микропараметрами идеального газа. Основное уравнение МКТ выражает выражает связь давления газа со средней кинетической энергией поступательного движения молекул. Давление газа на стенки сосуда является результатом многочисленных ударов молекул. При каждом ударе стенка получает силовой импульс, величина которого зависит от скорости молекул и, следовательно, от энергии их движения. При огромном числе ударов создается постоянное давление газа на стенку. Число ударов зависит от концентрации молекул n. Таким образом, можно ожидать, что давление газа связано с концентрацией молекул и с энергией их движения. Получим основное уравнение МКТ.

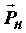
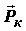
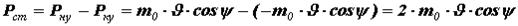
Рассмотрим сферический объём радиуса R, в котором находится N молекул идеального газа. Рассмотрим движение одной из них. Допустим, что молекула двигалась прямолинейно с импульсом ударилась о стенку под углом ψ к нормали и отскочила от неё под тем же углом, имея импульс . Найдём импульс, переданный молекулой стенке при ударе. Из закона сохранения импульса:

.

Путь, который молекула проходит от одного удара о стенку до другого, равен хорде АВ, т. е. величине 2Rcosψ.

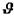
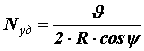
Найдем число ударов молекулы о стенку за одну секунду. Оно равно отношению скорости молекулы к пути, проходимому молекулой от одного столкновения со стенкой до другого:

.

Сталкиваясь со стенками сосуда, одна молекула за одну секунду сообщает ей импульс

Суммарный импульс, сообщенный всеми N молекулами стенке сосуда за одну секунду будет равен

.

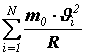
Из II закона Ньютона следует, что импульс, сообщённый за единицу времени стенке, численно равен силе, поэтому сила давления, действующая на поверхность сосуда, равна

.

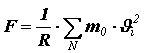
Давление найдём, разделив силу на площадь поверхности сферического сосуда:

,

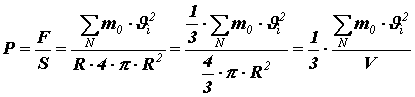
где 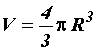– объём сосуда с газом.

Перепишем полученное равенство в виде:

Помножив и поделив правую часть на число молекул N в объёме V, получим:

или (9)

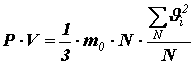
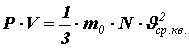
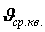
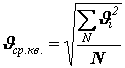
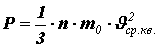
Здесь введена величина – средняя квадратичная скорость, равная корню квадратному из суммы квадратов всех скоростей, делённой на число молекул:

. (10)

, (11)

где n 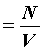–концентрация молекул.

Это уравнение называется основным уравнением молекулярно-кинетической теории идеального газа.

Получим связь давления со средней кинетической энергией поступательного движения молекулы

. (12)

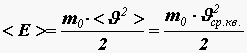
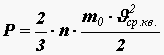
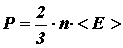
Из формулы (11) , следовательно:

. (13)

Таким образом, давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы. Это утверждение можно считать другой формулировкой основного уравнения молекулярно-кинетической теории идеального газа.

Рассмотрим газ, состоящий из молекул различных веществ, который находится в объёме V. Вследствие хаотического теплового движения молекулы каждой компоненты смеси будут распределены по объёму равномерно, т.е. так как если бы остальные компоненты газа отсутствовали. Из–за постоянных соударений молекул друг с другом, сопровождающихся частичным обменом между ними импульсами и энергиями, в смеси устанавливается тепловое равновесие. Всё это приводит к тому, что давление каждой из компонент смеси не будет зависеть от присутствия остальных.

Тогда результирующее давление определяется суммарным давлением всех компонентов, т.е. для смеси газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов.

, (14)

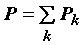
где k – номер газовой компоненты в смеси, Pk – ее парциальное давление, т.е. то давление, которое имел бы k–ый газ, если бы только он один занимал весь объём, занимаемый смесью.

Средняя квадратичная скорость молекул.

Из основного уравнения молекулярно-кинетической теории можно получить формулу для расчета средней квадратичной скорости молекул

.

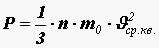
Произведение массы одной молекулы m0 на число молекул в единице объема n равно плотности вещества r : = r m0×n.

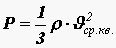
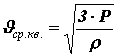
Таким образом, . Отсюда следует, что

. (15)

кспериментальные газовые законы

Изопроцессы. Законы Бойля-Мариотта, Гей-Люссака, Шарля.

Всякое изменение состояния газа называется термодинамическим процессом.

Простейшими процессами в идеальном газе являются изопроцессы. Это процессы, при которых масса газа и один из его параметров состояния (температура, давление или объем) остаются постоянными.

Изопроцесс, протекающий при постоянной температуре, называется изотермическим.

Экспериментально Р. Бойлем и Э. Мариоттом было установлено, что при постоянной температуре произведение давления газа на объем для данной массы газа есть величина постоянная (закон Бойля–Мариотта):

(16)

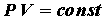
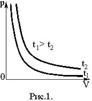
Графически этот закон в координатах РV изображается линией, называемой изотермой (рис.1).

Изопроцесс, протекающий в идеальном газе, в ходе которого давление остается постоянным, называется изобарным.

Зависимость объема газа от его температуры при постоянном давлении была установлена Л. Гей-Люссаком, который показал, что объем газа данной массы при постоянном давлении возрастает линейно с увеличением температуры (закон Гей-Люссака):

где V – объем газа при температуре t, °С; V0 – его объем при 0°С.

Величина 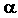называется температурным коэффициентом объемного расширения. Для всех газов  = (1/273°С–1). Следовательно,

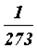
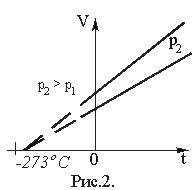
V = V0·(1 +·t). (18)

Графически зависимость объема от температуры изображается прямой линией – изобарой (рис. 2). При очень низких температурах (близких к – 273°С) закон Гей–Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.

Изопроцесс, протекающий в газе, при котором объем остается постоянным, называется изохорным.

Исследования зависимости давления данной массы газа от температуры при неизменном объеме были впервые проведены французским физиком Шарлем. Им было установлено, что давление газа данной массы при постоянном объеме возрастает линейно с увеличением температуры (закон Шарля):

P = P0(1+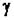t). (19)

Здесь P – давление газа при температуре t, °С; P0 – его давление при 0 °С.

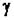
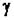
Величина называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов = 1/273 °С–1. Таким образом,

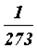
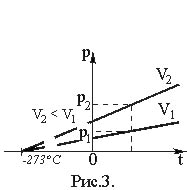
P = P0(1 +·t). (20)

Графическая зависимость давления от температуры изображается прямой линией – изохорой (Рис. 3).

Абсолютная шкала температур.

Если изохору продолжить в область отрицательных температур, то в точке пересечения с осью абсцисс имеем

P = P0(1 +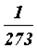·t) = 0. (21)

Отсюда температура, при которой давление идеального газа обращается в нуль, t = –273°С (точнее,–273,16°С). Эта температура выбрана в качестве начала отсчета термодинамической шкалы температур, которая была предложена английским ученым Кельвиным. Эта температура называется нулем Кельвина (или абсолютным нулем).

Температура, отсчитанная по термодинамической шкале температур, обозначается Т. Ее называют термодинамической температурой. Так как точка плавления льда при нормальном атмосферном давлении, принятая за 0°С, равна 273,16 К–1, то

Получим другую форму уравнений, описывающих изобарный и изохорный процессы, заменив в уравнениях (18) и (20) температуру, отсчитанную по шкале Цельсия, термодинамической температурой:

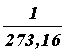
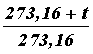
V = V0(1 + ·t) = V0() = V0

Обозначив объемы газа при температурах Т1 и Т2, как V1 и V2, запишем

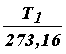
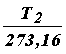
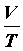
V1 = V0, V2 = V0.

= сonst. (23)

Аналогично получим новую форму закона Шарля :

(24)

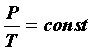
Законы Шарля и Гей-Люссака можно объединить в один общий закон, связывающий параметры P, V и T при неизменной массе газа.

Действительно, предположим, что начальное состояние газа при m = const характеризуется параметрами V1, Р1, Т1, а конечное – соответственно V2, Р2, Т2. Пусть переход из начального состояния в конечное состояние происходит с помощью двух процессов: изотермического и изобарического. В ходе первого процесса изменим давление с Р1 на Р2. Объем, который займет газ после этого перехода, обозначим V, тогда по закону Бойля–Мариотта, Р1V1 = Р2V, откуда

(25)

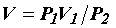
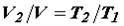
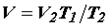
На втором этапе уменьшим температуру с Т1 до Т2, при этом объем изменится от значения V до V2; следовательно по закону Шарля откуда

(26)

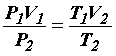
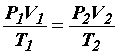
В уравнениях (25) и (26) равны левые части; следовательно, равны и правые, тогда , или

, (27)

т. е. можно записать, что

. (28)

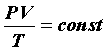
Выражение (28) называют уравнением Клапейрона или объединённым газовым законом.

Уравнение состояния идеального газа – уравнение Менделеева-Клапейрона.

Значение входящей в уравнение (28) константы, которая обозначается как R, для одного моля любого газа одинаково, поэтому эта константа получила название универсальной газовой постоянной.

Найдем числовое значение R в СИ, для чего учтем, что, как следует из закона Авогадро, один моль любого газа при одинаковом давлении и одинаковой температуре занимает один и тот же объем. В частности при Т0 = 273K и давлении Р0 = 105 Па объем одного моля газа равен V0 = 22,4·10–³ м³. Тогда R =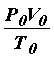= 8,31 Дж/(моль· К).

Уравнение (28) для одного моля газа можно записать в виде

. (29)

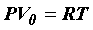
Из уравнения (29) легко получить уравнение для любой массы газа. Газ массой m займет объем V = V0(m/M), где М – масса 1 моль, m/M – число молей газа. Умножив обе части уравнения (29) на m/M, получим .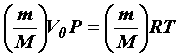

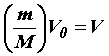
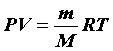
Так как , то окончательно получаем

. (30)

Уравнение (30) называется уравнением Менделеева – Клапейрона и является основным уравнением, связывающим параметры газа в состоянии теплового равновесия. Поэтому его называют уравнением состояния идеального газа.

Сравнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (для этого число молекул N возьмём равным числу Авогадро NА), найдём среднюю кинетическую энергию одной молекулы:

и .

. (31)

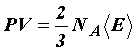
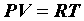
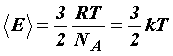
Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул.

Величина R/NА = k в уравнении (31) получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле:

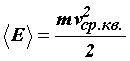
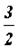
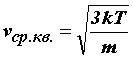
Так как =kТ, то средняя квадратичная скорость равна

. (32)

Подставляя значение средней кинетической энергии поступательного движения молекул (31) в основное уравнение молекулярно–кинетической теории газов, получим другую форму уравнения состояния идеального газа:

Давление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру.

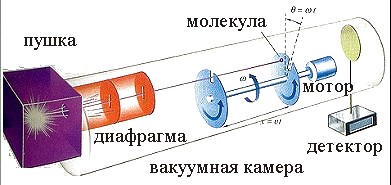
На рис. приведена схема опыта Штерна для определения скорости молекул газа.

Коган М.Н. Динамика разреженного газа. М., Физматлит, 1999

Кикоин А.К., Кикоин И.К. Молекулярная физика. М., Физматлит, 1976

Сивухин Д.В. Общий курс физики, т. 2. Термодинамика и молекулярная физика. М., Физматлит,

Источник