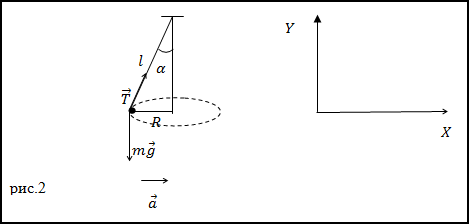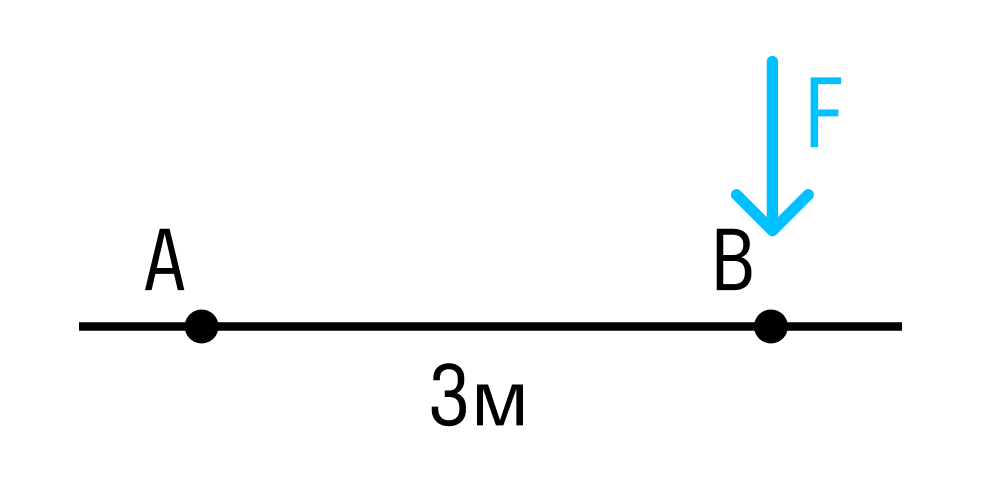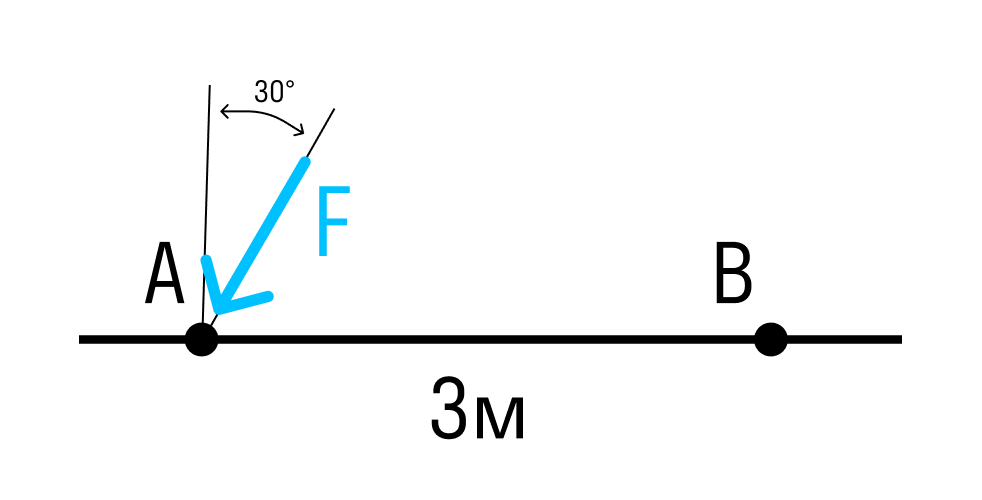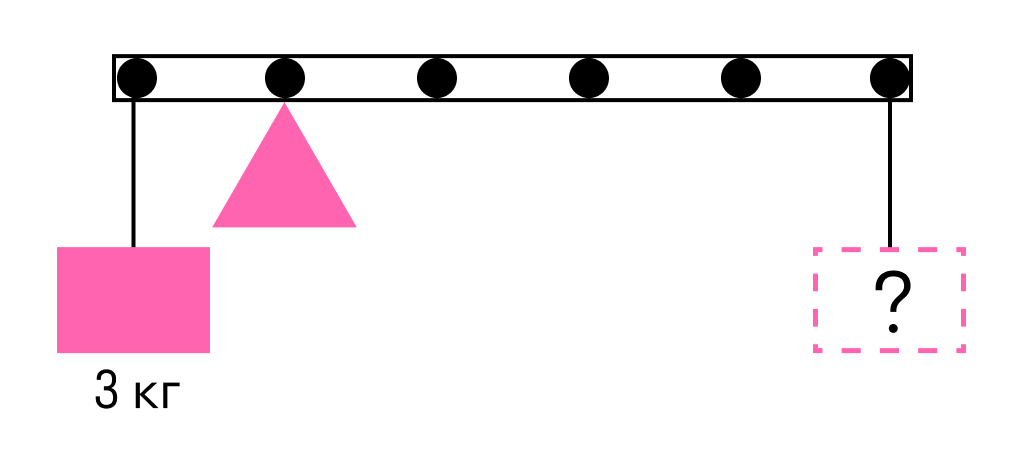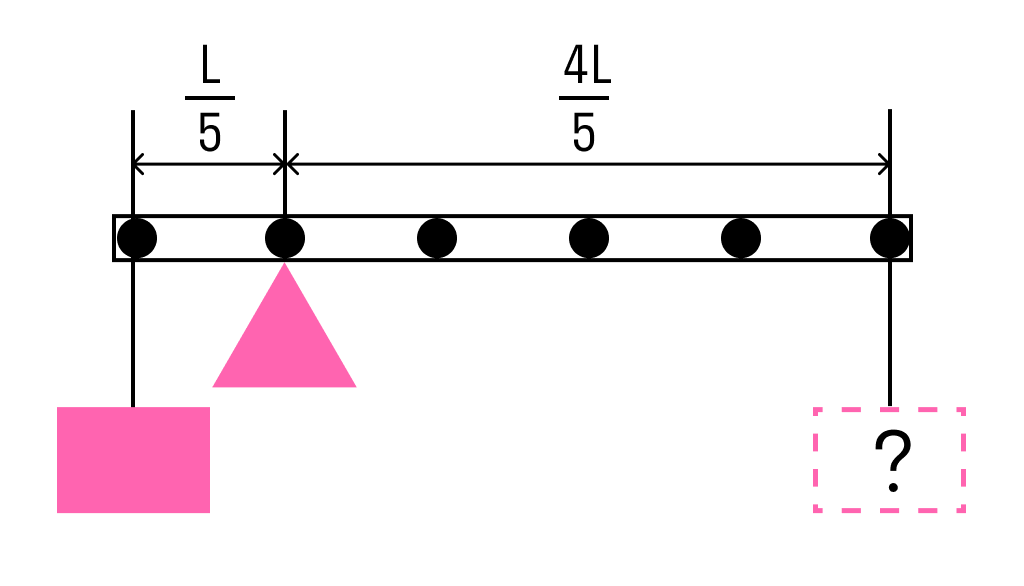Момент натяжения в чем измеряется
Формула силы натяжения нити
Определение и формула силы натяжения нити
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:
Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
Примеры решения задач
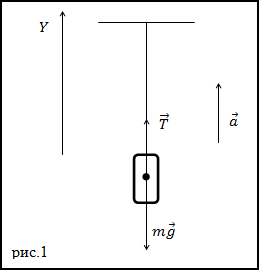
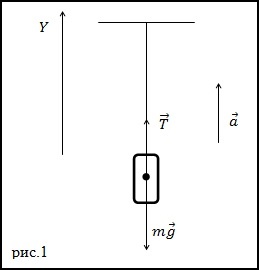
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
Из выражения (1.2) получим ускорение:
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
Ответ. a=1,2м/с 2
Формула силы натяжения нити не по зубам? Тебе ответит эксперт через 10 минут!
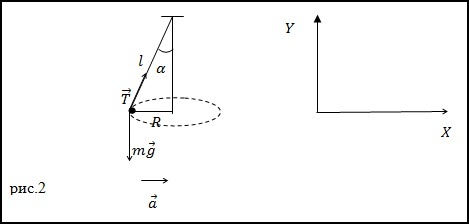
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
$$ \begin
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
Момент силы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.
Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.
На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.
То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
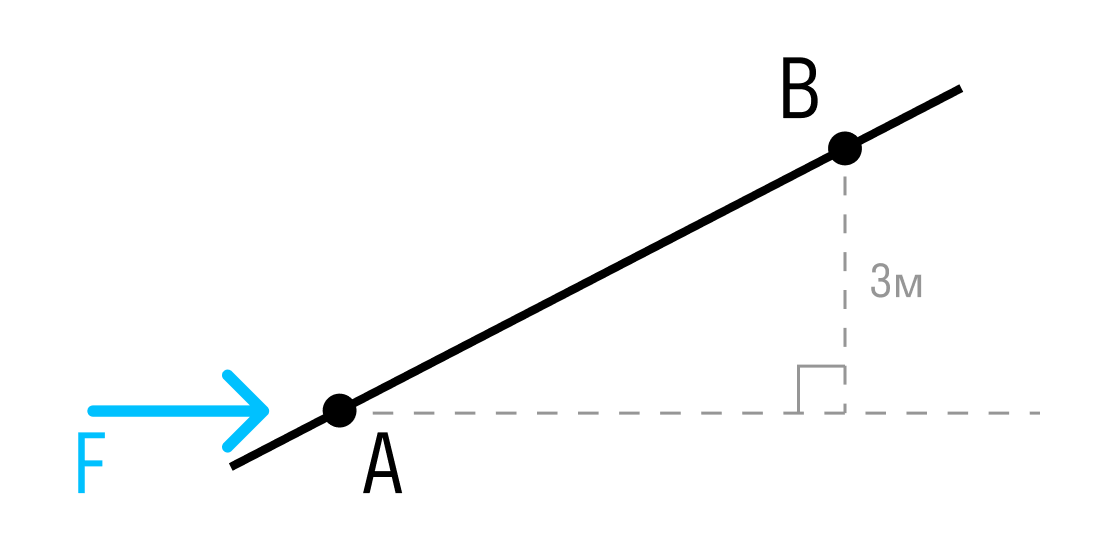
Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn = M’1 + M’2 +. + M’n
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
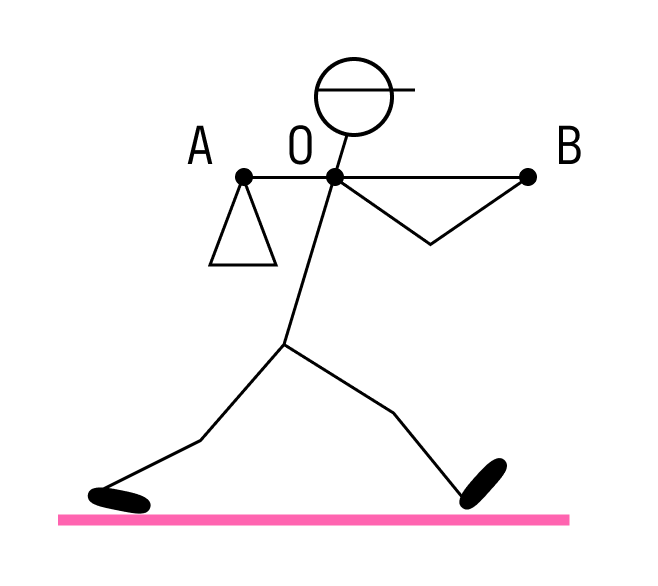
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
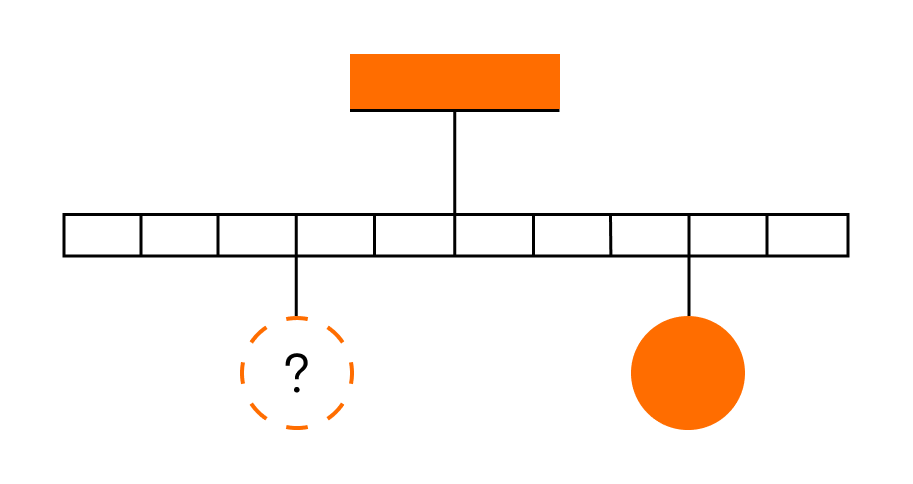
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага m1g*l1=m2g*l2
Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг
Ответ: Масса груза равна 0,3 кг
Задача 4
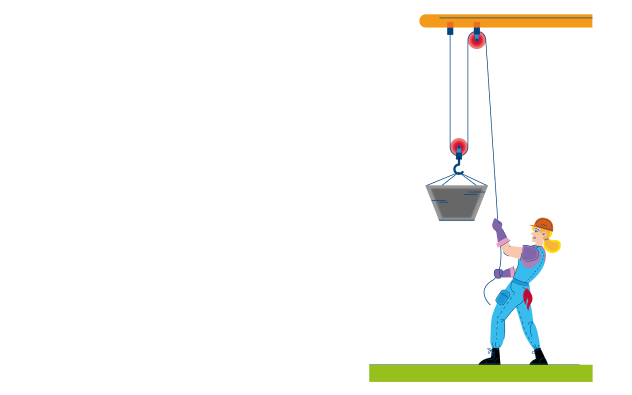
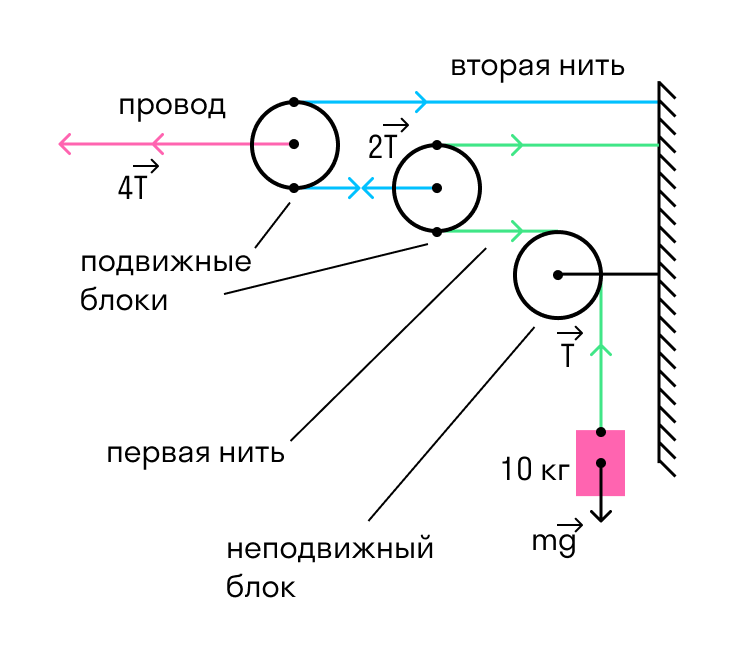
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?
Решение:
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н
Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно
Ответ: натяжение провода равно 400 Н
Задача 5 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
Определение силы натяжения нити
Сила натяжения нити — формулировка
Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.
Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
Сила натяжения во вращающейся системе
Описание
Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:
Формула расчета
Рассчитать силу натяжения в условиях вращающейся системы можно так:
Обозначение, единица измерения
Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)
Примеры решения задач
Задание 1
На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.
Решение
Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.
\(\bar
Проекция уравнения будет иметь следующий вид:
Данное выражение позволяет рассчитать ускорение:
Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления
Задание 2
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.
Решение
Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:
Проекции данной формулы по осям определяются следующим образом:
X: \(T sin α = ma = mω2R\)
Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:
Анализ рисунка позволяет вывести следующее уравнение:
\(\sin \alpha = \frac
Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:
Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:
Усилие затяжки болтов: расчет момента
Правильно затянутый болт — это тот, который затянут так, что он действует как очень ребристая пружина, стягивающая сопрягаемые поверхности вместе. Вращение болта (крутящий момент) в какой-то момент вызывает его растяжение (натяжение). На величину натяжения, возникающего при приложении заданного момента затяжки, влияет несколько факторов:
Если болт затянут достаточно, то соединение будет более надежным и прослужит дольше. При этом не будет деформированных деталей.
Требуемое осевое усилие болта
Соотношение между приложенным крутящим моментом и осевой силой или нагрузкой в болте может быть рассчитано по формуле T = K х F х d, где:
Следует иметь в виду, что табличные показатели обычно являются грубым расчетом. Кроме того, точность динамометрического ключа обычно не превышает +-25%.
Приведенный ниже расчет можно использовать для вычисления крутящего момента, необходимого для достижения заданного осевого усилия болта или нагрузки. Способ является универсальным и может использоваться для неметрических и метрических единиц измерения до тех пор, пока использование единиц измерения является последовательным.
Обратите внимание, что стандартные сухие крутящие моменты обычно рассчитываются для создания растягивающего напряжения или осевой силы, а также нагрузки зажима в болте, которая равна 70% минимальной прочности на растяжение или 75% запаса прочности.
Пример расчета: пробная нагрузка для метрического болта М30 является 373000 N. Крутящий момент, необходимый для достижения этого натяжения с помощью сухого болта, можно рассчитать следующим образом: Тсухой = (0,2) х (373000 Н) х (30 мм) х (10-3 м / мм) = 2238 (Н/м).
Смазка болта маслом SAE 30 уменьшает крутящий момент, необходимый для достижения того же напряжения, примерно на 40%. Уменьшенный крутящий момент можно рассчитать по формуле ТSAE30 = (2238 Н/м) х (1 – (40%) / (100%)) = 1343 Н/м.
Прочность болта
В следующей таблице приведены характеристики прочности для различных классов свойств метрических стальных болтов, винтов и шпилек:
Класс
Диапазон номинальных размеров (мм)
Прочность (МПа)
Предел растяжимости, мин (МПа)
Предел прочности при растяжении, мин (МПа)
Материал
Низкоуглеродистая или среднеуглеродистая сталь
Низкоуглеродистая или среднеуглеродистая сталь; полностью или частично отожженная
Низко- или среднеуглеродистая сталь; холодная обработка
Среднеуглеродистая сталь; закаленная
Среднеуглеродистая сталь; закаленная
Среднеуглеродистая сталь; закаленная
Легированная сталь; закаленная
Легированная сталь; закаленная
Предел прочности или предельная прочность на растяжение может быть определена как максимальная величина растягивающего напряжения, которое компонент может выдержать до того, как он сломается. Запас прочности может быть определен как наибольшая величина растягивающего напряжения, которое компонент способен выдержать до начала проявления пластической или постоянной деформации при снятии приложенного напряжения.
Предел растяжимости — это единица растягивающего напряжения, которое компонент может выдержать, когда он проявляет 0,2% пластической или постоянной деформации. Класс обычно штампуется на головке болта. Эти две цифры указывают на прочность болта или винта при предельном растяжении.
В случае болта класса 8.8 первая цифра означает, что предел прочности при растяжении составляет не менее 800 МПа. Вторая цифра означает, что крепеж начнет давать выход на 80% от предела прочности при растяжении, то есть не менее 640 МПа.
Контроль над затяжкой крепежа
Если гайки и болты, закрепляющие сменную деталь или механическую систему, имеют требуемое давление затяжки, то динамометрический ключ необходим по нескольким причинам. В большинстве случаев при попытках затянуть крепежные детали с помощью накидного ключа или ручного ключа-храповика произойдет две вещи:
Всегда при техническом обслуживании транспортного средства или другой конструкции лучше пользоваться заводским руководством. Инструкция позволит правильно выполнить необходимые действия, получив желаемый результат. А для крепления болтами деревянных элементов нужна шайба квадратная для деревянных конструкций. Это необходимо для того чтобы предотвратить образование вмятин в дереве и ослабления затяжки. На самом деле, лучше выполнять такое крепление саморезами. В нашем магазине «Первый крепеж» можно купить саморезы, опт цена на которые вас приятно удивит.
Вот несколько общих советов по использованию динамометрического ключа:
Чтобы затянуть болты повышенной прочности, зачастую требуется дополнительное оборудование, позволяющее усилить крутящий момент. Обычно в подобной ситуации применяется ключ-мультипликатор.
Таблица момента затяжки болтов
В таблице ниже указаны значения предварительной нагрузки и моменты затяжки для стальных крепежных деталей с тонкой метрической резьбой:
Класс свойств предварительной нагрузки (N) по стандарту ГОСТ Р ИСО 898-1-2011
Затяжка болтов динамометрическим ключом: таблицы, способы определения усилий
Чтобы увеличить прочность и срок эксплуатации резьбовых соединений, а также повысить их сопротивление различным внешним факторам необходимо правильно закрутить крепежные элементы, рассчитав усилие завинчивания. Каждое соединение имеет свою определенную степень затяжки в зависимости от посадочного места. Момент затяжки рассчитывается в зависимости от температурного режима, свойства материала и нагрузки, которая будет оказываться на резьбовое соединение.
К примеру, под воздействием температурных показателей металл начинает расширяться, а под воздействием вибрации на элемент оказывается дополнительная нагрузка. Соответственно, для минимизации воздействующих факторов, болты необходимо закручивать с расчетом правильного усилия. Предлагаем ознакомиться с таблицей силы затяжки болтов, а также методами и инструментами выполнения работ.
Что такое затяжное усилие и как его узнать?
Моментом затяжки называют показатель усилия, который необходимо приложить для резьбовых соединений в процессе их завинчивания. Если крепеж был закручен с прикладыванием небольшого усилия, чем это было нужно, то при воздействии различных механических факторов резьбовое соединение может не выдержать, теряется герметичность скрепленных деталей, что влечет за собой тяжелые последствия. Так же и при чрезмерном усилии, резьбовое соединение или скрепляемые детали могут попросту разрушиться, что приведет к срыву резьбы или появлению трещин в конструкционных элементах.
Каждый размер и класс прочности резьбовых соединений имеет определенный момент затяжки при работе с динамометрическим ключом, который указывается в специальной таблице. При этом обозначение класса прочности изделия располагается на его головке.
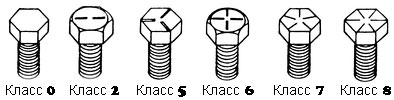
Маркировка и класс прочности деталей
Цифровое обозначение параметра прочности метрического болта указано на головке, и представлено в виде двух цифр через точку, к примеру: 4.6, 5.8 и так далее.
Предельная текучесть представляет собой максимальную нагрузку на конструкцию болта. Элементы, которые выполняются из нержавеющих видов стали, имеют обозначение непосредственно самого вида стали (А2, А4), и только после этого указывается предельная прочность.
К примеру, А2-50. Значение в подобной маркировке обозначает 1/10 прочностного предела углеродистой стали. При этом, изделия, для изготовления которых используется углеродистая сталь, имеют класс прочности – 2.
Обозначение прочности для дюймовых болтов отмечается насечками на его головке.
В чем измеряется затяжное усилие?
Основная величина измерения усилия затяжки болтов – Паскаль (Па). Международная система «СИ» предполагает, что данной единицей измеряется как давление, так и механическое напряжение. Соответственно, Паскаль равен значению давления, которое вызывается силой равной одному Ньютону и равномерным образом распределяется на плоскости размером в 1 м2.
Чтобы понять как можно конвертировать одну единицу измерения в другую, посмотрим пример:
Значения усилий затяжки для различных типов болтов (таблица)
Для более удобного и точного восприятия представлена таблица затяжки болтов динамометрическим ключом.
| Резьба | Класс прочности, Нм | Головка, мм | |||||||
| 3.6 | 4.6 | 5.8 | 6.8 | 8.8 | 9.8 | 10.9 | 12.9 | ||
| М5 | 1.71 | 2.28 | 3.8 | 4.56 | 6.09 | 6.85 | 8.56 | 10.3 | 8 |
| М6 | 2.94 | 3.92 | 6.54 | 7.85 | 10.5 | 11.8 | 14.7 | 17.7 | 10 |
| М8 | 7.11 | 9.48 | 15.8 | 19 | 25.3 | 28.4 | 35.5 | 42.7 | 13 |
| М10 | 14.3 | 19.1 | 31.8 | 38.1 | 50.8 | 57.2 | 71.5 | 85.8 | 17 |
| М12 | 24.4 | 32.6 | 54.3 | 65.1 | 86.9 | 97.7 | 122 | 147 | 19 |
| М14 | 39 | 52 | 86.6 | 104 | 139 | 156 | 195 | 234 | 22 |
| М16 | 59.9 | 79.9 | 133 | 160 | 213 | 240 | 299 | 359 | 24 |
| М18 | 82.5 | 110 | 183 | 220 | 293 | 330 | 413 | 495 | 27 |
| М20 | 117 | 156 | 260 | 312 | 416 | 468 | 585 | 702 | 30 |
| М22 | 158 | 211 | 352 | 422 | 563 | 634 | 792 | 950 | 32 |
| М24 | 202 | 270 | 449 | 539 | 719 | 809 | 1011 | 1213 | 36 |
Также представим таблицу момента затяжки для дюймовых видов резьб по стандарту, который применяется в Соединенных Штатах.
| Дюймы | Нм | Фунт |
| 1/4 | 12±3 | 9±2 |
| 5/16 | 25±6 | 18±4.5 |
| 3/8 | 47±9 | 35±7 |
| 7/16 | 70±15 | 50±11 |
| 1/2 | 105±20 | 75±15 |
| 9/16 | 160±30 | 120±20 |
| 5/8 | 215±40 | 160±30 |
| 3/4 | 370±50 | 275±37 |
| 7/8 | 620±80 | 460±60 |
Значения усилий затяжки для ленточного хомута с червячным зажимом
Ниже приведенная таблица содержит ряд данных про первоначальную установку ленточных хомутов на новом шланге, а также про повторную затяжку уже обжатых шлангов.
| Размер хомута | Нм | Фунт/Дюйм |
| 16мм — 0,625 дюйма | 7,5±0,5 | 65±5 |
| 13,5мм — 0,531 дюйма | 4,5±0,5 | 40±5 |
| 8мм — 0,312 дюйма | 0,9±0,2 | 8±2 |
| Усилие затяжки для повторных стяжек | ||
| 16мм | 4,5±0,5 | 40±5 |
| 13,5мм | 3,0±0,5 | 25±5 |
| 8мм | 0,7±0,2 | 6±2 |
Определение момента затяжки
Динамометрическим ключом
Подбор этого инструмента должен осуществляться так, чтобы затяжной момент на крепежном элементе был на 20-30% меньше, нежели значение максимального момента на используемом ключе. Если попытаться превысить допустимый лимит, то инструмент может легко сломаться.
Затяжное усилие и марка материала должны присутствовать на каждом изделии, способы расшифровки маркировки описаны выше.
Чтобы выполнить вторичную протяжку болтов, следует придерживаться следующих рекомендаций:
Без использования динамометрического ключа
Чтобы выполнить проверку нам понадобится наличие:
Момент затяжки является усилием, которое необходимо приложить на рычаг размером в 1 метр. К примеру, требуется выполнить затяжку гайки рассчитав для этого усилие в 2 кГс/м: