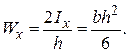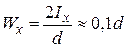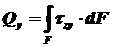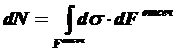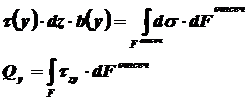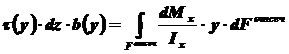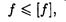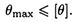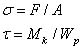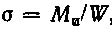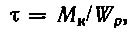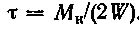Момент сопротивления в чем измеряется

Основы сопромата, момент сопротивления

10. Определение момента сопротивления.

Для абсолютного большинства строительных материалов значение расчетного сопротивления уже определено эмпирическим путем, поэтому определить параметры сечения, на которое действуют растягивающие или сжимающие напряжения, не сложно. Значения расчетных сопротивлений для большинства строительных материалов есть в разного рода справочниках, тем не менее при большом желании эти значения можно определить и самому.

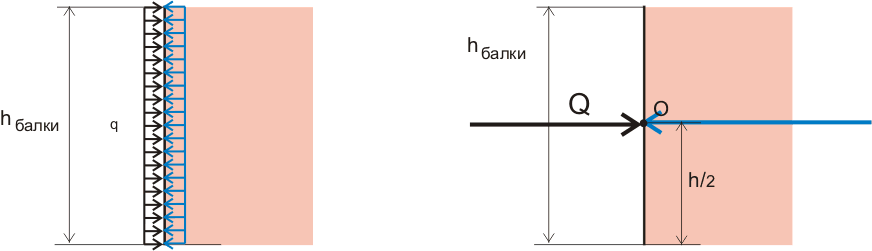
Рисунок 10.1. Внутренние напряжения в поперечном сечении балки.

В этом случае, если нам известна нагрузка и расчетное сопротивление материала, то можно легко определить площадь сечения конструкции:

S ≥ Q / R (10.1)

Пример №2. На поперечное сечение балки действует изгибающий момент, который можно заменить парой сил (рисунок 8.2) или распределенной нагрузкой, изменяющейся по высоте (рисунок 8.3). Т.е. растягивающие и сжимающие нормальные напряжения изменяются по высоте балки и поэтому использовать приведенную выше формулу нельзя, нужно как-то учитывать изменение внутренних напряжений в зависимости от высоты балки.

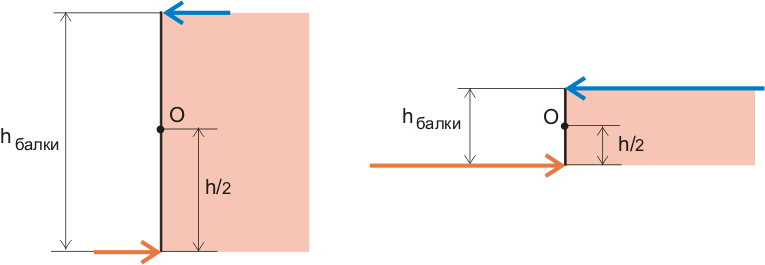
Рисунок 8.2. Увеличение значения сил при уменьшении высоты балки при одинаковом вращающем моменте.

Рисунок 8.3. Изменение распределенной нагрузки по высоте балки.

Для наглядности на пару минут вернемся к нашей линейке. Если мы возьмем линейку, которая лежала на книгах плашмя, поставим ее и приложим к линейке точно такую же нагрузку как и к лежащей плашмя линейке, то линейка вообще не прогнется, точнее прогнется, но увидеть это невооруженным глазом невозможно. В чем же дело? ведь ни нагрузка, ни длина балки и, соответственно, изгибающий момент, ни материал балки, ни сечение балки не изменились, изменилось только положение балки в пространстве. Теория сопротивления материалов объясняет это чудо так: при действии на балку нагрузки балка деформируется (прогибается), при этом верхняя часть балки сжимается и в этой части возникают сжимающие напряжения, а нижняя часть балки растягивается и в этой части возникают растягивающие напряжения. Эти напряжения называются нормальными, так как они направлены перпендикулярно поперечному сечению балки (по нормали).

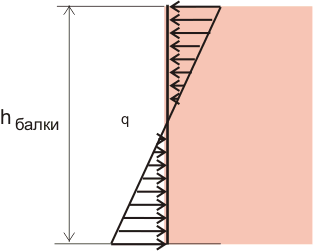
Конечно же при деформации балки в любом поперечном сечении возникают и касательные напряжения, направленные параллельно поперечному сечению (значение этих напряжений можно определить по эпюре «Q», рисунки 7.1 и 7.2), однако значение касательных напряжений при простом загружении в сечении, где действует максимальный изгибающий момент, равно нулю. При этом предполагается, что в некоторой точке (а точнее в ряде точек, которые находятся на оси z) поперечного сечения балки никаких деформаций нет, т.е. значение нормальных сжимающих или растягивающих напряжений равно 0, при этом максимальные сжимающие напряжения возникают в самом верхнем слое балки, а максимальные растягивающие напряжения возникают в самом нижнем слое балки. Графически это выглядит так:

Рисунок 10.2. Напряжения, возникающие в поперечном сечении балки при действии изгибающего момента.

Так как мы предполагаем для конструкции из однородного материала, что растягивающие напряжения суммарно равны сжимающим напряжениям и при этом площадь на которую действуют растягивающие напряжения, равна площади, на которую действуют сжимающие напряжения. То определить значение момента сопротивления мы можем следующим образом. Сначала сведем линейно-изменяющиеся нормальные напряжения к равнодействующим, обозначим их как Р:

Р_σс = Р_σр = P = (bh/2)σ/2 = bhσ/4 (10.2)

Тогда момент сопротивления для двух равнодействующих сил, действующих относительно центра тяжести сечения, составит:

W’ = 2Py (10.3)

Как известно на все тела, живые и неживые, в пределах планеты Земля действует сила тяжести. Например, если линейка которую мы все никак не можем доломать, весит 50 г, то это означает, что на линейку действует сила тяжести 0.5 Н или 0.05 кгс. Кроме того, пока никто не опровергнул и предположения, что на каждый отдельный атом, молекулу и любую другую часть материи действует своя сила тяжести, при этом общая сила тяжести линейки равна сумме сил тяжести всех атомов или других частиц, входящих в состав этой линейки. Далее, чтобы линейка не падала на землю под воздействием силы тяжести, мы должны сделать опору для линейки хотя бы в одной точке. Точка эта не простая, получается, что сумма моментов, возникающих при действии сил тяжести, действующих на каждую частицу линейки, в этой точке равна нулю. Таким образом соблюдается условие равновесия системы. Вполне логично эта точка называется центром тяжести. Например, для нашей линейки центр тяжести находится в геометрическом центре линейки. Но сейчас нас интересует центр тяжести не прямоугольника, а треугольника, который символизирует внутренние напряжения или линейно изменяющуюся равномерную нагрузку. Как утверждает наука геометрия, центр тяжести треугольника находится на пересечении медиан углов треугольника, при этом расстояние от любого острого угла до высоты, опущенной на катет, равно 2/3 длины этого катета (рисунок 8.2). Так как мы рассматриваем не все поперечное сечение балки, а только верхнюю (или нижнюю половину), то

у = (h/2)(2/3) = h/3 (10.4)

Теперь, когда мы определили значение плеча силы, мы можем подставить его в формулу (4.3) и определить момент сопротивления для нашей балки прямоугольного сечения относительно оси z:

W’_z = 2(bhσ/4)h/3 = σbh 2 /6 (10.5)

Примечание: как правило момент сопротивления рассматривается как геометрическая характеристика сечения. Т.е. нормальные напряжения в формуле опускаются (W_z = W’_z/σ). Почему, мы узнаем чуть позже.

Момент сопротивления сечения можно определять и как отношение момента инерции относительно оси z к максимальному расстоянию от оси z до наиболее удаленных точек сечения.

W_z = I_z / (h/2) = (bh 3 /12)/(h/2) = bh 2 /6 (10.6)

Итак, в ходе долгих, хотя и не сложных вычислений мы определили, что

М = W’ или M/W’ = 1 или Мσ/W = σ (10.7)

А так как внутренние нормальные напряжения σ должны быть меньше или в крайнем случае равны расчетному сопротивлению материала (σ ≤ R), то формула (4.7) будет иметь несколько иной вид:

М/W = Mσ/W’ ≤ R или W ≥ M/R (10.8)

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Просто благодарна вам за ваш труд, просто восполняю пробелы в знаниях, хотя, имею сертификат конструктора. Сделала небольшой перевод на карту ПБ Украины.

Инна, и вам большое спасибо.

Напишите номер банковские карты

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

МОМЕНТ СОПРОТИВЛЕНИЯ

геом. хар-ка поперечного сечения стержня (балки, вала), определяющая его сопротивляемость в рассматриваемом сечении изгибу или кручению и равная осевому (или полярному) моменту инерции, делённому на расстояние от оси (или центра тяжести) до наиболее удалённой точки сечения. М. с. применяют в ф-лах сопротивления материалов и строит. механики.

Смотреть что такое «МОМЕНТ СОПРОТИВЛЕНИЯ» в других словарях:

Момент сопротивления — – отношение момента инерции относительно определенной оси сечения к расстоянию от центра тяжести сечения до точки на линии, перпендикулярной оси (проходящей через центр тяжести), максимально удаленной от центра тяжести сечения. [Полякова, Т … Энциклопедия терминов, определений и пояснений строительных материалов

момент сопротивления — atsparumo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Konstrukcijos elemento skerspjūvio geometrinė charakteristika, rodanti elemento atsparumą lenkimui arba sukimui. atitikmenys: angl. moment of resistance vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

момент сопротивления — atsparumo momentas statusas T sritis fizika atitikmenys: angl. moment of resistance vok. Widerstandsmoment, n rus. момент сопротивления, m pranc. moment résistant, m … Fizikos terminų žodynas

МОМЕНТ СОПРОТИВЛЕНИЯ — геометрическая характеристика поперечного сечения стержня, показывающая сопротивляемость стержня в рассматриваемом сечении изгибу или кручению (Болгарский язык; Български) съпротивителен момент (Чешский язык; Čeština) průřezový modul; modul… … Строительный словарь

МОМЕНТ СОПРОТИВЛЕНИЯ ПЛАСТИЧЕСКИЙ — момент сопротивления в поперечном сечении изгибаемого стержня, определяемый из условия образования в сечении пластического шарнира (Болгарский язык; Български) пластичен съпротивителен момент (Чешский язык; Čeština) plastický průřezový modul… … Строительный словарь

момент сопротивления (тормозной) вращающегося электродвигателя — 3.9 момент сопротивления (тормозной) вращающегося электродвигателя : Вращающий момент на валу электродвигателя, действующий так, чтобы снизить частоту вращения двигателя. Источник: СТО 70238424.29.160.30.002 2009: Электродвигатели. Организация… … Словарь-справочник терминов нормативно-технической документации

момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus antrajam ploto momentui, padalytam iš atstumo nuo ašies iki toliausiai nuo jos esančio ploto taško. atitikmenys: angl. section modulus vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis fizika atitikmenys: angl. section modulus vok. Widerstandsmoment gegen Biegung, n rus. момент сопротивления сечения, m pranc. module résistant, m … Fizikos terminų žodynas

Момент сопротивления качению колеса — 72. Момент сопротивления качению колеса Mf Источник: ГОСТ 17697 72: Автомобили. Качение колеса. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

момент сопротивления сечения — [section modulus] геометрическая характеристика поперечного сечения тела, равная отношению момента инерции к расстоянию от оси наиболее удаленной точки сечения. Смотри также: Момент момент прокатки момент количества движения момент инерции … Энциклопедический словарь по металлургии

Источник

Момент сопротивления

Нормальные напряжения зависят только от изгибающего момента, а касательные только от поперечной силы. Это позволяет упростить расчет нормальных напряжений для частного случая чистого изгиба, когда Q = 0.

Волокна, не изменяющие своей длины, образуют нейтральный слой. Линии пересечения нейтрального слоя с плоскостью сечения балки называется нейтральная ось.

Расчет балок на прочность проводится по максимальным нормальным напряжениям, возникающим в тех поперечных сечениях, где наибольший изгибающий момент.

Для балок из хрупких материалов составляют два условия прочности:

Распределение нормальных нагрузок по сечению таково, что часть материала, находящегося около нейтральной оси, почти не нагружена. Наиболее целесообразно использовать двухтавровое поперечное сечение, для которого с наименьшими затратами материала можно получить наибольший момент сопротивления.

37 вопрос- Расчет на прочность при изгибе

При изгибе балки происходит искривление ее оси в плоскости действия внешней силы.

J_z — экваториальный момент инерции сечения балки относительно оси z.

Величина EJ_zназывается жесткостью бруса при изгибе.

Исключая кривизну из предыдущей формулы получим выражение для напряжения:

Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии

Отношение J_z/y_max называется моментом сопротивления сечения при изгибе и обозначается через W_х :

Эта формула является основной при расчете на прочность бруса при изгибе.

Для бруса прямоугольного сечения J_z = bh 3 /12

Для бруса круглого сечения J_z = πD 4 /64

38 вопрос- Поперечный изгиб

Поперечный изгиб – это такой вид нагружения, при котором в поперечных сечениях бруса возникают не только изгибающие моменты Мх, но и поперечные силы Qу. Эта сила представляет собой равнодействующую элементарных распределенных сил, лежащих в плоскости сечения. В этом случае в поперечных сечениях возникают не только нормальные, но и касательные напряжения.

Возникновение касательных напряжений τ сопровождается появлением угловых деформаций. Поэтому, кроме основных смещений, свойственных чистому изгибу, каждая элементарная площадка сечения dF получает еще некоторые дополнительные угловые смещения, обусловленные сдвигом (рис. 10.16).

Рис. 10.16 Искривление поперечных сечений

При поперечном изгибе моменты, возникающие в левом и правом сечениях элемента, не одинаковы и отличаются на dM. Продольным горизонтальным сечением, проведенным на расстоянии у от нейтрального слоя, разделим элемент на две части и рассмотрим условия равновесия верхней части. Равнодействующая нормальных сил 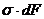в левом сечении в пределах заштрихованной площади (отсеченной части) равна

Полагая, что справедливо распределение в виде:

, получим

,

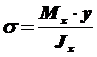
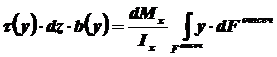
где через у обозначена текущая ордината площадки dF. Разность нормальных сил в правом и левом сечении должна уравновешиваться касательными силами, возникающими в продольном сечении элемента (рис. 10.19)

39 вопрос –Линейные и угловые перемещения при изгибе

Под действием поперечных нагрузок продольная ось искривля­ется (рис. 33.6). Если материал подчиняется закону Гука, после сня­тия нагрузок брус выпрямляется, поэтому изогнутую ось бруса назы­вают упругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.

При прямом поперечном изгибе бруса его ось, искривляясь, оста­ется в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол Θ.

Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонталь­ные перемещения сечений ничтожно малы и не учитываются. Рассмат­ривают вертикальные перемещения центра тяжести сечения, называе­мые прогибами (у). Максимальные прогибы обозначают f = у_таx. Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.

Условие жесткости выражается неравенством

Существует несколько методов определения перемещений сече­ний при изгибе. Один из них основан на дифференцировании урав­нения упругой линии, более рациональный способ — использование интегралов Мора. Метод Мора — универсальный способ определения линейных и угловых перемещений в любых системах.

Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.

При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для кото­рых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.

Ограничение угла поворота вводится для обеспечения нормаль­ной работы подшипников скольжения и роликовых подшипников.

В этом случае проверяется дополнительное условие жесткости:

Определение линейных и угловых перемещений необходимо для расчетов на жесткость при изгибе и нахождения так называемых лишних неизвестных в статически неопределимых балках.

40 вопрос- Напряженное состояние в точке

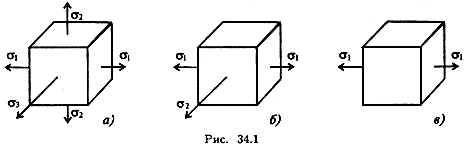
Напряженное состояние в точке характеризуется нормальными и касательными напряжениями, возникающими на всех площадках (сечениях), проходящих через данную точку. Обычно достаточно определить напряжения на трех взаимно перпендикулярных площадках, проходящих через рассматриваемую точку. Точку принято изображать в виде маленького элемента в форме параллелепипеда (рис. 34.1).

Положения теории напряженного состояния:

1. Напряженное состояние в данной точке полностью определено, если известны напряжения по любым трем взаимно перпендикулярным площадкам.

2. Среди множества площадок, которые можно провести через данную точку, есть три такие взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения, эти площадки называются главными, а нормальные напряжения, возникающие на них, называются главными напряжениями: σ₁; σ₂; σ₃ (рис. 34.1).

Одно из этих напряжений — максимально, одно — минимально. Максимальное обозначают σ₁, минимальное — σ₃.

Классификация видов напряженного состояния производится по главным напряжениям:

— если все три главных напряжения не равны нулю, то напряженное состояние называют объемным (трехосным) (рис. 34.1а);

— если одно из главных напряжений равно нулю, напряженное состояние называют плоским (двухосным) (рис. 34.15);

— если два из главных напряжений (σ₂ = 0) противоположны по знаку, напряженное состояние называют упрощенным плоским состоянием;

— если лишь одно из главных напряжений не равно нулю, на­пряженное состояние линейное (рис. 34.1 в).

41 вопрос- Сложное деформированное состояние

Сложное деформированное состояние возникает в тех случаях, когда элемент конструкции или машина подвергается одновременно нескольким простейшим деформациям.

Выше рассматривались заклепочные и шпоночные соединения, в которых одновременно возникает срез и смятие и соответственно действуют нормальные и касательные напряжения. В затянутых болтах также имеет место сложное деформирование, в них обнаруживается совместное действие растяжения от затяжки силой F и кручения от момента трения Мк. В связи с этим в болтах возникают нормальные напряжения от растяжения и касательные напряжения от кручения

где 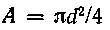— площадь сечения болта; — полярный момент сопротивления.

Нормальные напряжения распределены по сечению равномерно, а касательные достигают максимальных значений у контура болта. Очевидно, периферийные точки болта находятся в наиболее опасном состоянии, особенно в связи с наличием концентрации напряжений в нарезке.

Другим примером сложного деформирования являются валы, которые работают на изгиб и кручение. При этом в поперечном сечении вала возникают нормальные и касательные напряжения. Возникающие от изгиба нормальные напряжения достигают максимального значения в волокнах, наиболее удаленных от нейтральной оси:

где Ми — изгибающий момент; 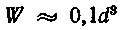— осевой момент сопротивления сечения.

Максимальные касательные напряжения при кручении возникают в точках контура поперечного сечения

где Wp = 0,2d^3 — полярный момент сопротивления.

Следовательно, в наиболее напряженных точках вала при совместном действии изгиба,и кручения возникают нормальные и касательные напряжения. Встает вопрос, какое же из этих напряжений или какая их комбинация определяют прочность вала. Ответ на этот вопрос дают так называемые теории (или гипотезы) прочности.

42 вопрос- Устойчивость сжатых стержней

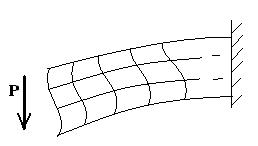
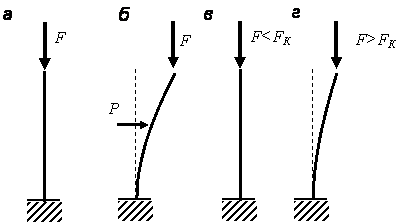
Деформированное состояние центрально-сжатого стержня (рис. 8.1, а) может быть устойчивым или неустойчивым. Если вывести стержень из первоначального состояния малой дополнительной горизонтальной силойР, то он окажется искривлённым (рис. 8.1, б). После удаления силы Р стержень либо возвращается в первоначальное прямолинейное состояние (рис. 8.1, в), либо остаётся искривлённым (рис. 8.1, г). Первый случай соответствует устойчивому деформированному состоянию стержня, второй случай – неустойчивому деформированному состоянию.

Рис. 8.1. Состояния сжатого стержня: а – исходное; б – стержень с дополнительной поперечной нагруз­кой Р; в – прямолинейный стержень после удаления силы Р; г – криволинейный стержень после удале­ния силы Р

Между устойчивым и неустойчивым состояниями теоретически существует промежуточное, называемоекритическим состоянием, при котором стержень после удаления силы Р может остаться в равновесии как в прямолинейном состоянии, так и в криволинейном. При заданных размерах стержня вид его деформированного состояния зависит от величины сжимающей силы.

Наибольшая величина сжимающей силы, при которой деформированное состояние стержня ещё устойчивое, называется критической силой, обозначаемой F_К (рис. 8.1)

Превышение величины критической силы приводит к потере устойчивости, при которой малые поперечные нагрузки приводят к большим изгибным перемещениям стержня и возможному его разрушению.

Отношение критической силы к площади поперечного сечения стержня называют критическим напряжением .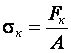

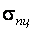
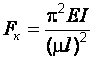
В том случае, когда критические напряжения не превышают предела пропорциональности материала , потеря устойчивости начинается при упругом деформировании стержня и критическую силу вычисляют по формуле Эйлера

,

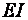
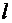
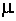
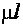
где _– изгибная жёсткость; – геометрическая длина стержня; – коэффициент приведения длины стержня, зависящий от способов закрепления концов стержня (табл. 8.1). Произведение называется приведённой длиной стержня.

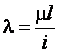
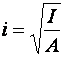
Для сжатых стержней вводится безразмерная характеристика, называемая гибкостью , где – радиус инерции поперечного сечения.

Формула Эйлера справедлива при условии .

43 вопрос- Расчет на устойчивость сжатых стержней.Критическая сила.

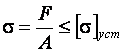
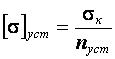
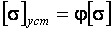
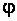
Для сжатых стержней должно выполняться условие устойчивости , в котором допускаемые напряжения на устойчивость получаются делением критических напряжений на коэффициент запаса устойчивости . Принято выражать величину через величину основных допускаемых напряжений при расчетах на прочность , где множитель называется коэффициентом продольного изгиба. Этот коэффициент зависит от гибкости и материала стержня, его величина меньше единицы и находится из справочных таблиц.

Для практических расчётов условие устойчивости записывают в виде

.

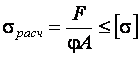
Наибольшая величина сжимающей силы, при которой деформированное состояние стержня ещё устойчивое, называется критической силой, обозначаемой F_К (рис. 8.1)

Превышение величины критической силы приводит к потере устойчивости, при которой малые поперечные нагрузки приводят к большим изгибным перемещениям стержня и возможному его разрушению.

Отношение критической силы к площади поперечного сечения стержня называют критическим напряжением .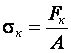

44 вопрос – Критическое напряжение при расчете на устойчивость сжатых стержней

Превышение величины критической силы приводит к потере устойчивости, при которой малые поперечные нагрузки приводят к большим изгибным перемещениям стержня и возможному его разрушению.

Отношение критической силы к площади поперечного сечения стержня называют критическим напряжением .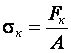

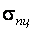
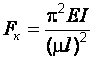
В том случае, когда критические напряжения не превышают предела пропорциональности материала , потеря устойчивости начинается при упругом деформировании стержня и критическую силу вычисляют по формуле Эйлера

,

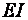
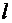
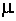
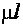
где _– изгибная жёсткость; – геометрическая длина стержня; – коэффициент приведения длины стержня, зависящий от способов закрепления концов стержня (табл. 8.1). Произведение называется приведённой длиной стержня.

45 вопрос- Сопротивление усталости.Понятие о цикле.

Для оценкисопротивления усталости материалов, предназначенных для производства энергетических установок, химического и другого оборудования, нами [80] разработана методика и создано оборудование для испытания материалов на усталость при периодическом смачивании, нагретых до повышенных температур образцов, брызгами коррозионной среды. [7]

Совокупность термодинамических процессов, в результате которых рабочее тело возвращается в исходное состояние, называется термодинамическим циклом, или круговым процессом.

46 вопрос- Факторы влияющие на сопротивление усталости

Сопротивление усталости материалов в общем случае зависит от трех групп факторов, связанных, во-первых, с характером напряженного состояния детали или образца, во-вторых, со свойствами материала, и, в-третьих, с воздействием окружающей среды. Причины остановки роста усталостной трещины целесообразно рассматривать с учетом именно этих групп факторов.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник